About

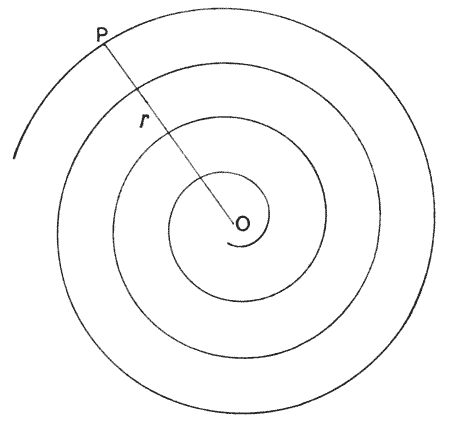
One of the key mathematical ideas discussed in On Growth and Form is the logarithmic spiral (also known as the equiangular spiral). In this type of spiral, the distance between the whorls continually increases. This is due to twisting at a constant rate but growing at a constant acceleration. This happens in nature, for instance, in the Nautilus shell. In such cases the new, growing tissue is added to the end of old, already hardened, tissue.
The new tissue does not change the shape of the shell, the shape of it remains continually similar during all of its growth.
This allows the shell to grow asymmetrically (it grows at one end only), while retaining its unchanging form.

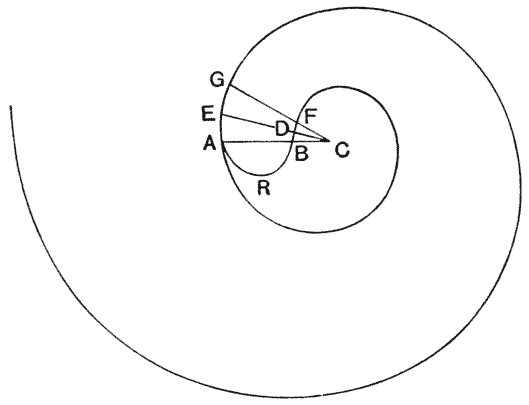
The logarithmic spiral differs from the more commonly seen Archimedes spiral where there is a constant distance between the whorls. The difference can be seen in the diagrams below.

The logarithmic spiral was first discovered by the French scientist René Descartes in 1638.
On Growth and Form concentrates on the natural occurrences of this spiral. It is seen in the form of animal horns, teeth and tusks, as well as in the shells of molluscs and spiders' webs.

Correspondents

William Peddie