Peter Barlow: Theory of Numbers
Peter Barlow's first book was An Elementary Investigation of the Theory of Numbers published in 1811. In fact the book had a much longer title which in full read as An Elementary Investigation of the Theory of Numbers with its Application to the Indeterminate and Diophantine Analysis, the Analytical and Geometrical Division of the Circle, and several other Curious Algebraical and Arithmetical Problems by Peter Barlow, The Royal Military Academy, London, 1811.
It appears that "Theory of Numbers" in the title of this book is the first occurrence of this phrase in English although Legendre wrote Essai sur la théorie des nombres in 1798.
We give below a version of Barlow's Preface to this work. Before this, however, we make a few comments. He claims in the Preface to give a proof of the general case of Fermat's Last Theorem in Chapter 6. He had first published this "proof" in 1810 and had then incorporated the "proof" into his book. Of course, this must contain an error. In fact, his attempt to prove the impossibility of the general case of Fermat's Last Theorem involved the error that a sum of fractions in their lowest terms is not an integer if the denominator of each fraction has a factor not dividing all the remaining denominators. Barlow was, however, able to give a correct proof of the case providing an alternative to Fermat's proof of this case.
Let us be rather mean and point out another error in the book. On page 299 it is stated that the equation has its smallest solution with the values
If the above makes it appear that Barlow's book is rather poor, this is certainly not so for, despite the errors, it is a well written book which is still worth reading today. We also note that the brief history of number theory and its current status that Barlow gives in the Preface make interesting reading as it shows clearly the position at the beginning of the 19th century.
It appears that "Theory of Numbers" in the title of this book is the first occurrence of this phrase in English although Legendre wrote Essai sur la théorie des nombres in 1798.
We give below a version of Barlow's Preface to this work. Before this, however, we make a few comments. He claims in the Preface to give a proof of the general case of Fermat's Last Theorem in Chapter 6. He had first published this "proof" in 1810 and had then incorporated the "proof" into his book. Of course, this must contain an error. In fact, his attempt to prove the impossibility of the general case of Fermat's Last Theorem involved the error that a sum of fractions in their lowest terms is not an integer if the denominator of each fraction has a factor not dividing all the remaining denominators. Barlow was, however, able to give a correct proof of the case providing an alternative to Fermat's proof of this case.
Let us be rather mean and point out another error in the book. On page 299 it is stated that the equation has its smallest solution with the values
,
These values are not correct. The correct values are
Let us also point out that a comment Barlow makes in the book appears to us today to be rather comical. Barlow states that Euler's prime number
,
is the greatest that will ever be discovered, for, as they are merely curious without being useful, it is not likely that any person will attempt to find one beyond it.
Well, we can't blame Barlow for not being good at predicting the future!
is the greatest that will ever be discovered, for, as they are merely curious without being useful, it is not likely that any person will attempt to find one beyond it.
If the above makes it appear that Barlow's book is rather poor, this is certainly not so for, despite the errors, it is a well written book which is still worth reading today. We also note that the brief history of number theory and its current status that Barlow gives in the Preface make interesting reading as it shows clearly the position at the beginning of the 19th century.
An Elementary Investigation of the Theory of Numbers
PREFACE
The Theory of Numbers is a subject which has engaged the attention and exercised the talents of many celebrated mathematicians, both ancient and modern; under the first of which classes, may be reckoned Pythagoras and Aristotle, the former of whom is said to have invented our present multiplication table, or the Abacus Pythagoricus of the ancients; though what is alluded to under this designation was probably a much more extensive table than that now in common use: Pythagoras also attributed to numbers certain mystical properties, and seems first to have conceived the idea of what are now termed magic squares. Aristotle, amongst other numerical speculations, noticed the uniformity in almost all nations of dividing numbers into periods of tens, and attempted an explanation of the cause of this singular coincidence upon philosophical principles.
But the earliest regular system of numbers is that given by Euclid in the 7th, 8th, 9th and 10th books of his Elements, which, notwithstanding the embarrassing notation of the Greeks, and the inadequacy of geometry to the investigation of numerical propositions, is still very interesting, and displays, like all the other parts of the same celebrated work, that depth of thought and accuracy of demonstration for which its author is so eminently distinguished.
Archimedes likewise paid particular attention to the powers and properties of numbers as may be seen by consulting his tract entitled "Arenarius," in which some modern Writers have thought they could perceive inculcated the principles of our present system of logarithms; but all that can be allowed on this head is, that the method by which he performed his multiplications and divisions bears a considerable analogy to that which we now commonly employ in the multiplication and division of powers; that is, by the addition and subtraction of their indices.
Before the invention of analysis, however, no very extensive progress could be made in a subject, which required so much generality of investigation; and, accordingly, we find but little was effected in it till the time of Diophantus, whose treatise of algebra contains many interesting problems in the more abstruse parts of this science. But here also, its author had to encounter the difficulties of a complicated notation, and a very deficient analysis, when compared with that of the present period; and, therefore, it cannot be expected that his work should contain a complete investigation of the theory of numbers.
After Diophantus, the subject remained unnoticed, or at least unimproved, till Bachet, a French analyst of considerable reputation, undertook the translation of the abovementioned work into Latin, retaining also the Greek text, which was published by him in 1621, interspersed with many marginal notes of his own, and which may be considered as containing the first germ of our present theory. These were afterwards considerably extended by the celebrated Fermat, in his edition of the same work, published, after his death, in 1670, where we find many of the most elegant theorems in this branch of analysis; but they are generally left without demonstration, an omission which he accounted for by stating, in one of his notes, page 180, that he was himself preparing a treatise on the theory of numbers, which would contain many new and interesting numerical propositions; but, unfortunately, this work never appeared, and most of his theorems remained without demonstration for a considerable time.
At length, the subject was again revived by Euler, Waring, and Lagrange, three of the most eminent analysts of modern times. The former, besides what is contained in the second volume of his "Elements of Algebra," and his "Analysis Infinitorum" has several papers in the Petersburg Acts, in which are given the demonstrations of many of Fermat's theorems. What has been done by Waring on this subject is comprised in chap. v. of his "Meditationes Algebraicae;" and Lagrange, who has greatly extended the theory of numbers, by the invention of many new propositions, has several interesting papers on this head, in the Memoirs of Berlin, besides what are contained in his additions to Euler's Algebra.
It is, however, but lately that this branch of analysis has been reduced into a regular system, a task that was first performed by Legendre, in his "Essai sur la Theorie des Nombres;" and nearly at the same time Gauss published his "Disquisitiones Arithmeticae:" these two works eminently display the talents of their respective authors, and contain a complete development of this interesting theory. The latter, in particular, has opened a new field of inquiry, by the application of the properties of numbers to the solution of binomial equations, of the form
on the solution of which depends the division of the circle into n equal parts, as was before known from the Cotesian theorem. This solution he has accomplished in several partial cases, whence the division of the circle into a prime number of equal parts is performed, by the solution of equations of inferior dimensions; and when the prime number is of the form , the same may be done geometrically, a problem that was far from being supposed possible before the publication of the abovementioned performance.
From the foregoing historical sketch, it appears that the writers on this subject are far from being numerous; but the well established celebrity of those, who have investigated its principles, would be of itself sufficient to stamp it with a degree of importance, and to render it worthy of attention. Few persons, it is conceived, will be disposed to consider that a barren subject, which has so much engaged the attention of the above named celebrated writers; in fact, there is no branch of analysis that furnishes a greater variety of interesting truths than the theory of numbers, and it is therefore singular that it should have been so little attended to by English mathematicians. With the exception of what is contained in vol. ii. of Euler's Algebra, and the notes added to the second English edition of that work, there is nothing on this subject to be found in our language.
This circumstance, it is conceived, will be deemed a sufficient apology for the appearance of the present volume; in which, if I have, in certain theorems, availed myself of what others have done on the same subject, yet it is presumed, that it will be found to possess a sufficient degree of novelty, both in matter and arrangement, to exempt me from the imputation of being a mere copyist.
With the exception of a few theorems, what is contained in the first six chapters may be considered as new: in the latter of which will be found a demonstration of Fermat's general theorem, on the impossibility of the indeterminate equation
,
for every value of greater than 2; the leading principle of which I first demonstrated in the Appendix to Euler's Algebra, and afterwards completed in vol. xxvii. of the Philosophical Journal. I also consider as original what is contained in chapter x., with the exception of that part relating to the arithmetic of the Greeks, for which I have been indebted to the Essay of Delambre, subjoined to the French translation of the works of Archimedes. The methods of solving indeterminate equations of the first degree, and of ascertaining, a priori, the number of possible solutions, have likewise some claim to novelty. In the other parts of the work, there will also be found several new theorems, and many former ones differently demonstrated, where simplicity and perspicuity could be attained by such alteration: this is particularly the case in the last chapter relating to Gauss's celebrated theorem on the division of the circle. Perspicuity has, indeed, been one of my principal objects; for this treatise being intended for the instruction and amusement of those who may not possess a very extensive knowledge of analysis, it became necessary to make it as clear and intelligible as possible: but how far I may have succeeded in my design, or what merit may be otherwise due to the performance in general, must be left to the decision of the public.
It only remains now for me to mention a circumstance, that may probably be thought to stand in need of some explanation: it will be perceived that I have introduced two new symbols, the necessity for which, however, will, I trust, appear upon a slight inspection of the work itself: the words of the form of recur very often, and the repetition of them would have been tedious and irksome to the reader, for which reason the double f (ff) is introduced instead of them, but, for the sake of uniformity, it is placed lengthwise thus,
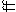 this, therefore, can scarcely be considered as an innovation of a very important rule laid down by modern analysts, "Not to multiply without necessity the number of mathematical symbols." And the same apology may be made for the introduction of the other sign, for the words divisible by. These characters were adopted on the suggestion of Mr Bonnycastle, Professor of Mathematics in the Royal Military Academy, to whose judgment and experience I have been greatly indebted for many important remarks relating to the present performance, and on various other occasions.
this, therefore, can scarcely be considered as an innovation of a very important rule laid down by modern analysts, "Not to multiply without necessity the number of mathematical symbols." And the same apology may be made for the introduction of the other sign, for the words divisible by. These characters were adopted on the suggestion of Mr Bonnycastle, Professor of Mathematics in the Royal Military Academy, to whose judgment and experience I have been greatly indebted for many important remarks relating to the present performance, and on various other occasions.
PETER BARLOW
Royal Military Academy, Woolwich,
October 1, 1811.
Last Updated October 2016