Judita Cofman on teaching mathematics
We present below the introduction to two of Judita Cofman papers on teaching mathematics to young children. Both were published in 1980, at a time when she was teaching at Putney High School, London. The third extract we give is taken from Cofman's 1996 paper On the Role of Geometry in Contemporary Mathematical High School Education.
1. The Christmas Tree.
Here is the problem that Judita Cofman describes in her paper 'Mathematics and the Christmas Tree (A Classroom Experience)', Mathematics in School 9 (4) (1980), 22-23:
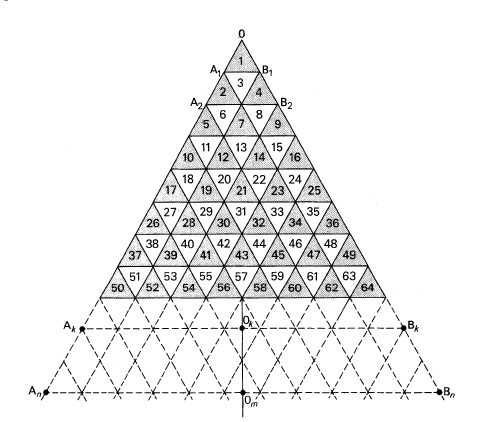
From time to time I try to organise a session of free activities in class. The pupils (aged 11 to 16) are given a "model" and asked to write down their observations and comments, possibly accompanied by suggestions for future projects. Our last model consisted of a set of congruent equilateral triangles arranged into an equilateral triangular shape as shown in the Figure.
The number of rows in the shape was unlimited. The triangles were numbered and the translated images of AA, OB, were shaded. My aim was to find out:
a) would the pupils be more attracted by geometric shapes or by properties of numbers included in Figure 1, and
b) would there be any attempts to apply knowledge on geometry to detect facts about numbers, or vice versa.
2. Pangrams.
Here is the problem that Judita Cofman describes in her paper 'Tangram and Pangram (Experience of a Maths Club)', Mathematics in School 9 (5) (1980), 25-27:
Tangram, the ancient Chinese puzzle, is frequently described in textbooks of school mathematics. It consists of seven tangram pieces: five isosceles right-angled triangles, a square and a parallelogram fitted in a square. A tangram shape is a flat shape consisting of all seven tangram pieces. In 1942 two Chinese mathematicians Fu Traing Wang and Chuan Chih Hsiung proved the following result:
A. There are 13 different convex polygonal tangram shapes.
In our Maths Club for young teenagers the following part of result A was verified:
B. There is no convex polygonal tangram shape with more than eight sides.
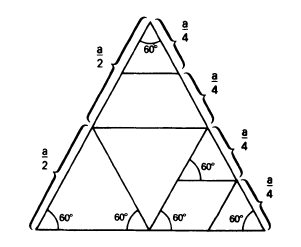
For the proof of B, properties of angles and their sums in convex polygonal tangram shapes were used. Further information on non-existence of convex polygonal tangram shapes could be obtained by investigating their perimeters and areas. This would involve arguments on irrational numbers, too sophisticated for the Maths Club. In search of a similar, but simpler puzzle we have constructed Pangram.
(P in honour of Putney High School), a modification of Tangram and stated the following problem:
C. Find all convex polygonal pangram shapes.
It seems to me that the study of Problem C in a junior Maths Club can be recommended for the following reasons:
(a) a complete solution to Problem C can be provided - this is rewarding, and
(b) there are different mathematical ideas involved in the process of the solution, which is inspiring.
In our Maths Club for young teenagers the following part of result A was verified:
B. There is no convex polygonal tangram shape with more than eight sides.

For the proof of B, properties of angles and their sums in convex polygonal tangram shapes were used. Further information on non-existence of convex polygonal tangram shapes could be obtained by investigating their perimeters and areas. This would involve arguments on irrational numbers, too sophisticated for the Maths Club. In search of a similar, but simpler puzzle we have constructed Pangram.
(P in honour of Putney High School), a modification of Tangram and stated the following problem:
C. Find all convex polygonal pangram shapes.
It seems to me that the study of Problem C in a junior Maths Club can be recommended for the following reasons:
(a) a complete solution to Problem C can be provided - this is rewarding, and
(b) there are different mathematical ideas involved in the process of the solution, which is inspiring.
3. On the Role of Geometry in Contemporary Mathematical High School Education.
- In the contemporary education, with a curriculum overburdened with details from various fields of mathematics, there is a danger that the study of mathematics can stray into memorizing facts and a mechanical learning of algorithms. Contrary to this, the efforts should be directed at pupils' understanding the existing links between the phenomena they encounter in different fields of mathematical study. Geometry can play a certain role in such efforts, because the mathematical disciplines taught in high school are rich in details for which there are geometrical illustrations appropriate to the pupils' age. The application of such illustrations, on the one hand, facilitates the process of understanding of the totality of teaching material, and on the other, presents geometry as a science of an actual importance.
- The importance of Euclidean geometry in teaching is supported by the fact that the shapes of this geometry are encountered in our living environment. The study of space is particularly facilitated by the study of solid geometry, which is, unfortunately, often neglected in syllabus and curriculum. There is an important fact in respect to geometrical features of space which is often forgotten; the majority of children possess a lot of elementary knowledge about objects, such as the cube or the sphere from the earliest age. This elementary knowledge can be extremely useful for introducing notions such as: defined and undefined elements, axioms and theorems, necessary and sufficient conditions, etc. All these notions are important for the field of mathematics while the familiarity with space can be used to make pupils grasp the essence starting from concrete examples.
- Mathematics is one of the earliest scientific disciplines, an important segment of human cultural heritage. This fact must be reflected on the teaching of mathematics: it is advisable to draw pupils' attention, whenever an opportunity arises, to their historical background. The history of geometry is an important part of the history of mathematics, not only because geometry is one of the oldest branches of mathematics. The importance of geometry mostly lies in the fact that there were several major problems in this field, starting from the Ancient Greek age, which could finally be solved only in the 19th century. The solutions to these problems had been sought for ages; the attempts led to a series of new discoveries and contributed to a further development of the entire science of mathematics. One of the famous problems of geometry was the so called Delian problem of doubling the cube.
- Teaching of geometry can also play a useful role in illustrating the achievements in the most current fields of mathematics.
- The knowledge gained in the study of geometry can contribute to a better understanding of the phenomena from different fields of natural sciences.
- For teaching of geometry to be successful, teaching personnel must have a solid knowledge of this subject. However, not only at schools, but also in university courses and other pedagogical institutions for training future mathematics teachers, there is a tendency of neglecting the study of geometry. This fact can lead to a drastic deterioration in the level of geometry teaching at schools. What is needed is an effort at elevating the respectability of geometry with the students of mathematics.
Last Updated August 2016