Persi Diaconis: St Andrews Honorary Degree
On Friday 13 September, Persi Diaconis was awarded an honorary degree during a special graduation ceremony which formed part of the University of St Andrews' 600th Anniversary celebrations. He was one of seventeen "international scholars and thinkers", "some of the best minds of our generation", who were honoured in this way. Here is laureation address by Nik Ruskuc, School of Mathematics and Statistics, University of St Andrews:
PROFESSOR PERSI DIACONIS
Mathematician & Statistician, Stanford University.
When mathematics is mentioned many here will perhaps not know what to think. On the one hand we are told it is all around us, affecting every aspect of our lives, and indeed we have all been subjected to it continually and painfully throughout our schooling. And on the other it seems beyond our reach, impenetrable, containing things like:
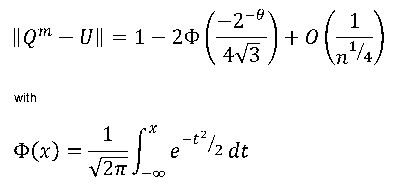
If I am permitted the audacity to try and capture in a sentence someone who is infinitely more knowledgeable and clever than me, I would say that Professor Diaconis has devoted his life to teaching us the difference between knowledge and magic.
Professor Diaconis was born in 1945 in New York. Early on he played violin, which he stopped, never to touch it again; he ran away from home at the age of 14, school unfinished, to join the famous magician Dai Vernon, for two years; he obtained the school diploma without asking for one, courtesy of his teachers. Yet he abandoned magic to study mathematics because he bought a copy of Feller's Probability which he wanted to understand but could not. He therefore applied to a number of mathematics departments and just one which offered statistics; nonetheless he ended up studying statistics because he 'wanted to go to Harvard'.
In an interview in 1984, when asked 'What does the future hold for Persi Diaconis?' he responded, 'Just going crazy, working hard, learning more math.' And that is how it went: appointments in Stanford and Harvard (currently a Joint Professorship in Statistics and Mathematics at Stanford), over 200 publications, around 40 doctoral students, tens of collaborators, always travelling, and always learning and sharing more mathematics.
A distinguishing feature of Professor Diaconis' work is his ability to bring together many disparate areas of mathematics, such as probability and group theory, statistics and combinatorics. His early fascination with magic also remains a prominent strand in Professor Diaconis' oeuvre, with many of his notable papers on the surface appearing to be about games and card tricks, but in fact developing deep theory and bringing out surprising insights into regularities emerging from random processes. The formula shown earlier is from Professor Diaconis' famous 1992 paper with Dave Bayer, Trailing the Dovetail Shuffle to its Lair. In it they answer the question: how many times do you need to riffle-shuffle an ordinary pack of 52 cards so that the resulting pack is truly random? The answer is seven, in a very strict and precise sense which is explained in the paper.
As is appropriate, professional admiration and recognition abound: Rollo Davidson Prize; MacArthur Fellowship; Fellow of the Institute of Mathematical Statistics; American Academy of Arts and Sciences; American Statistical Association; National Academy of Sciences; American Philosophical Society; American Mathematical Society; President, Institute of Mathematical Statistics; honorary degrees from Chicago, Toulouse, Uppsala, Queen Mary University London, Athens; Plenary Speaker, International Congress of Mathematicians.
But that is not the main thing. Let us listen again to Professor Diaconis himself: 'You know, to prepare for this interview I got out my curriculum vitae and looked at what I've been doing. I guess I feel happy about it. I think statistics is a beautiful rich field. How could you work in all the different areas that I've been allowed to work in, and still call yourself one thing - a statistician. The field is rich enough to allow that and even support it. You can do work in group theory and number theory, and do work in applied perception psychology, and it's all part of probability and statistics. I have no plans to do anything other than what I'm doing, which is going 20 hours a day and hoping to keep up with myself. I'm still fascinated by problems and trying to understand in my own language what the elders have been doing, hoping to relate that to what the youngsters are doing.' And in the preface to his wonderful new book entitled Magical Mathematics: '[I] make a living doing mathematics; teaching, proving, and conjecturing.'
After all this, it may come as something of a surprise that when asked about performing tricks in class Professor Diaconis answers: 'So I noticed that for me, mathematics and teaching don't go so well with magic.'
But in fact, this is not surprising at all. In fact, if I understand correctly what Professor Diaconis is telling us, this is the point: while both magic and mathematics are mysterious, entertaining and thought provoking at first, the former is essentially about averting the gaze and maintaining the mystery, while mathematics is about dispelling it and enabling others to see and think.
Laureator: ( Professor Nik Ruskuc, School of Mathematics and Statistics.
Last Updated September 2013