Napier's rods
 In 1617 Napier published Rabdologia. In it he explained how to use 'Napier's rods' which could be used to multiply numbers together where the calculator only needed to use addition. Napier dedicated the book to Alexander Seton, Earl of Dunfermline and explained in an introduction that he:-
In 1617 Napier published Rabdologia. In it he explained how to use 'Napier's rods' which could be used to multiply numbers together where the calculator only needed to use addition. Napier dedicated the book to Alexander Seton, Earl of Dunfermline and explained in an introduction that he:-
... was induced to publish a description of the construction and use of the numbersing rods because many of my friends, to whom I have already shown them, were so pleased with them that the rods are already almost common and are even being carried to foreign countries.
'Napier's rods' consisted of 10 rectangular blocks with multiples of a different digit on each of the four sides. For example the top of one of the rods on which multiples of 4 are given is shown here.
The other three sides of this rod had multiples of other digits. Note that, except for the top square, each square is divided by a diagonal, and when the digit 4 is multplied by 3 the resulting 12 is written with the 1 above a diagonal and the 2 below. All two digit numbers appear on the rods in the same way with the 10s digit above the diagonal and the unit digit below.
Glaisher, in an article in Encyclopaedia Britannica, described the way that the numbers were placed on each of the four sides of the ten rods:-
Napier's rods or bones consist of ten oblong pieces of wood or other material with square ends. Each of the four faces of each rod contains multiples of one of the nine digits, and is similar to [the one shown above], the first rod containing the multiples of 0, 1, 9, 8, the second of 0, 2, 9, 7, the third of 0, 3, 6, 9, the fourth of 0, 4, 9, 5, the fifth of 1, 2, 8, 7, the sixth of 1, 3, 8, 6, the seventh of 1, 4, 8, 5, the eighth of 2, 3, 7, 6, the ninth of 2, 4, 7, 5, and the tenth of 3, 4, 6, 5. Each rod, therefore, contains on two of its faces multiples of digits which are complementary to those on the other two faces; and the multiples of a digit and its complement are reversed in position.Let us explain how the rods were used. For example to multiply 4138 by 567 place four rods with the digits 4, 1, 3, 8 on top as shown alongside a strip containing the numbers 1 to 9 in squares
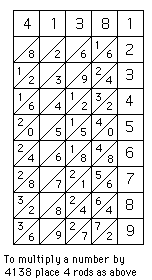
To multiply a number by 4138 place 4 rods as shown
To multiply 4138 by 567 we now examine rows 5, 6 and 7 of the four rods (as indicated by the right hand strip). Looking at row 5, starting from the right, we write down the number obtained by adding the digits in the parallellograms as shown.
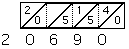
Next do the same with row 6, this time noting that we have to carry 1 when we add 8 + 4.
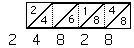
Place the numbers so that the second starts one place to the right of the first as shown
20690 24828
20690 24828 28966
20690 24828 28966 2346246
Now this may not seem a great saving in effort but, as we mentioned above, only addition is needed to carry out calculations. Napier's rods became quite popular and we used in Britain and on the Continent. The Rabdologia was translated into Italian and Dutch, and the original Latin text was republished in Leiden.
We have used the name 'Napier's rods' in this article, but often the calculating aid was called 'Napier's bones'. The name comes from the title of a work by William Leybourne publiahed in 1667 entitled The art of numbering by speaking rods: vulgarly termed Napier's bones. Why did Leybourne use the term 'speaking rods'? This was simply a mistranslation of Napier's Rabdologia. This comes from 'rabdos' meaning a 'rod' and 'logia' meaning 'collection'. However Leybourne thought it came from 'rabdos' meaning a 'rod' and 'logos' meaning 'word'.
Let us note that Napier also designed "square root rods" and "cube root rods" but these did not become so popular.
Often Napier's rods would come in a box which contained other tables and aids for calculation. For example one set made in 1679 came in a box 12 cms by 6.4 cms by 2.8 cms. The box had a hinged lid which had, on the outside, a table giving the interest at 6 per cent for one, two, three, six, and twelve months, for each £10 from 10 to 90, and for hundreds of pounds to £500. The bottom of the box had two tables on it, one giving the year, week day, age of the moon on 1 January for 1679 to 1693, and a "Perpetual Almanac" with the year beginning in March. The second table gave the time of high tide at various places relative to the age of the moon. Inside the lid of the box is a table for addition in 13 columns of eleven numbers, the first numbered downwards from 1 to 10, the next from 1 to 11 and so on to the thirteenth numbered from 12 to 22.
Last Updated August 2006