Carl Runge: Graphical Methods
Carl Runge gave a course of lectures on Graphical Methods at Columbia University in New York which were published by Columbia University Press in 1912. Below we give Runge's Introduction to the work in which he relates his interesting ideas on pure and applied mathematics in general. We then give a list of contents for the book, followed by the first section of Chapter I on Graphical Arithmetic. This gives the flavour of Runge's approach:
COLUMBIA UNIVERSITY LECTURES
KAISER WILHELM PROFESSOR OF GERMAN HISTORY AND INSTITUTIONS
FOR THE YEAR 1909-1910
GRAPHICAL METHODS
BYCARL RUNGE, Ph.D.
PROFESSOR OF APPLIED MATHEMATICS IN THE UNIVERSITY OF GÖTTINGENKAISER WILHELM PROFESSOR OF GERMAN HISTORY AND INSTITUTIONS
FOR THE YEAR 1909-1910
NEW YORK
COLUMBIA UNIVERSITY PRESS
1912
COLUMBIA UNIVERSITY PRESS
1912
INTRODUCTION
§ 1. A great many if not all of the problems in mathematics may be so formulated that they consist in finding from given data the values of certain unknown quantities subject to certain conditions. We may distinguish different stages in the solution of a problem. The first stage we might say is the proof that the quantities sought for really exist, that it is possible to satisfy the given conditions or, as the case may be, the proof that it is impossible. In the latter case we have done with the problem. Take for instance the celebrated question of the squaring of the circle. We may in a more generalized form state it thus: Find the integral numbers, which are the coefficients of an algebraic equation, of which is one of the roots. Thirty years ago Lindemann showed that integral numbers subject to these conditions do not exist and thus a problem as old almost as human history came to an end. Or to give another instance take Fermat's problem, for the solution of which the late Mr Wlolfskehl, of Darmstadt, has left $25,000 in his will. Find the integral numbers that satisfy the equation
,
where is an integral number greater than two. Fermat maintained that it is impossible to satisfy these conditions and he is probably right. But as yet it has not been shown. So the solution of the problem may or may not end in its first stage.
In many other cases the first stage of the solution may be so easy, that we immediately pass on to the second stage of finding methods to calculate the unknown quantities sought for. Or even if the first stage of the solution is not so easy, it may be expedient to pass on to the second stage. For if we succeed in finding methods of calculation that determine the unknown quantities, the proof of their existence is included. If on the other hand, we do not succeed, then it will be time enough to return to the first stage.
There are not a small number of men who believe the task of the mathematician to end here. This, I think, is due to the fact that the pure mathematician as a rule is not in the habit of pushing his investigation so far as to find something out about the real things of this world. He leaves that to the astronomer, to the physicist, to the engineer. These men, on the other hand, take the greatest interest in the actual numerical values that are the outcome of the mathematical methods of calculation. They have to carry out the calculation and as soon as they do so, the question arises whether they could not get at the same result in a shorter way, with less trouble. Suppose the mathematician gives them a method of calculation perfectly, logical and conclusive but taking 200 years of incessant numerical work to complete. They would be justified in thinking that this is not much better than no method at all. So there arises a third stage of the solution of a mathematical problem in which the object is to develop methods for finding the result with as little trouble as possible. I maintain that this third stage is just as much a chapter of mathematics as the first two stages and it will not do to leave it to the astronomer, to the physicist, to the engineer or whoever applies mathematical methods, for this reason that these men are bent on the results and therefore they will be apt to overlook the full generality of the methods they happen to hit on, while in the hands of the mathematician the methods would be developed from a higher standpoint and their bearing on other problems in other scientific inquiries would be more likely to receive the proper attention.
The state of affairs today is such that in a number of cases the methods of the engineer or the surveyor are not known to the astronomer or the physicist, or vice versa, although their problems may be mathematically almost identical. It is particularly so with graphical methods, that have been invented for definite problems. A more general exposition makes them applicable to a vast number of cases that were originally not thought of.
In this course I shall review the graphical methods from a general standpoint, that is, I shall try to formulate and to teach them in their most generalized form so as to facilitate their application in any problem, with which they are mathematically connected. The student is advised to do practical exercises. Nothing but the repeated application of the methods will give him the whole grasp of the subject. For it is not sufficient to understand the underlying ideas, it is also necessary to acquire a certain facility in applying them. You might as well try to learn piano playing only by attending concerts as to learn the graphical methods only through lectures.
TABLE OF CONTENTS
§ 1. Introduction
CHAPTER I. Graphical Calculation.
§ 2. Graphical arithmetic
§ 3. Integral functions
§ 4. Linear functions of any number of variables
§ 5. The graphical handling of complex numbers
CHAPTER II. The Graphical Representation of Functions of One or More Independent Variables
§ 6. Functions of one independent variable
§ 7. The principle of the slide rule
§ 8. Rectangular coordinates with intervals of varying size
§ 9. Functions of two independent variables
§ 10. Depiction of one plane on another plane
§ 11. Other methods of representing relations between three variables
§ 12. Relations between four variables
CHAPTER III. The Graphical Methods of the Differential and Integral Calculus.
§ 13. Graphical integration
§ 14. Graphical differentiation
§ 15. Differential equations of the first order
§ 16. Differential equations of the second and higher orders
CHAPTER I
GRAPHICAL CALCULATION
§ 2. Graphical Arithmetic. - Any quantity susceptible of mensuration can be graphically represented by a straight line, the length of the line corresponding to the value of the quantity. But this is by no means the only possible way. A quantity might also be and is sometimes graphically represented by an angle or by the length of a curved line or by the area of a square or triangle or any other figure or by the anharmonic ratio of four points in a straight line or in a variety of other ways. The representation by straight lines has some advantages over the others, mainly on account of the facility with which the elementary mathematical operations can be carried out.
What is the use of representing quantities on paper? It is a convenient way of placing them before our eye, of comparing them, of handling them. If pencil and paper were not as cheap as they are, or if to draw a line were a long and tedious undertaking, or if our eye were not as skilful and expert an assistant, graphical methods would lose much of their significance. Or, on the other hand, if electric currents or any other measurable quantities were as cheaply and conveniently produced in any desired degree and added, subtracted, multiplied and divided with equal facility, it might be profitable to use them for the representation of any other measurable quantities, not so easily produced or handled.
The addition of two positive quantities represented by straight lines of given length is effected by laying them off in the same direction, one behind the other. The direction gives each line a beginning and an end. The beginning of the second line has to coincide with the end of the first, and the resulting line representing the sum of the two runs from the beginning of the first to the end of the second. Similarly the subtraction of one positive quantity from another is effected by giving the lines opposite directions and letting the beginning of the line that is to be subtracted coincide with the end of the other. The result of the subtraction is represented by the line that runs from the beginning of the minuend to the end of the subtrahend. The result is positive when this direction coincides with that of the minuend, and negative when it coincides with that of the subtrahend. This leads to the representation of positive and negative quantities by lines of opposite direction. The subtraction of one positive quantity from another may then be looked upon as the addition of a positive and a negative quantity. I do not want to dwell on the logical explanation of this subject, but I want to point out the practical method used for adding a large number of positive and negative quantities represented by straight lines of opposite direction. Take a straight edge, say a piece of paper folded over so as to form a straight edge, mark a point on it, and assign one of the two directions as the positive one. Lay the edge in succession over the different lines and run a pointer along it through an amount equal in each case to the length of the line and in the positive or negative direction according to the sign of the quantity. The pointer is to begin at the point marked. The line running from this point to where the pointer stops represents the sum of the given quantities. The advantage of this method is that the intermediate positions of the pointer need not be marked provided only that the pointer keeps its position during the movement of the edge from one line to the next.
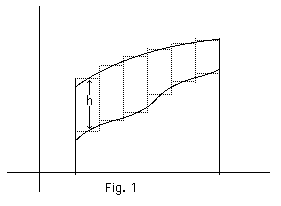
As an example take the area, Fig. 1. A number of rectangular strips 1/2 cm. wide are substituted for the area so that, measured in square centimetres, it is equal to half the sum of the lengths of the strips measured in centimetres. The straight edge is placed over the strips in succession and the pointer is run along them. The edge is supposed to carry a centimetre scale and the pointer is to begin at zero. The final position of the pointer gives half the value of the area in square centimetres. The drawing of the strips may be dispensed with, their lengths being estimated, only their width must be shown. If the scale should be too short for the whole length, the only thing we have to do is to break any of the lengths that range over the end of the scale and to count how many times we have gone over the whole scale. I have found it convenient to use a little pointer of paper fastened on the runner of a slide rule so that it can be moved up and down the metrical scale on one side of the
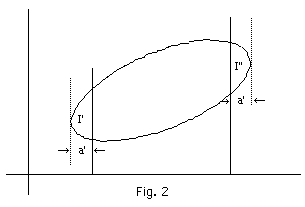
slide rule. The area is in this manner determined rapidly and with considerable accuracy, very well comparable to the accuracy of a good planimeter. If the area of any closed curve is to be found, the way to proceed is to choose two parallel lines that cut off two segments on either side (see Fig. 2), to measure the area between them by the method described above and to estimate the two segments separately. If the curves of the segments may with sufficient accuracy be regarded as arcs of parabolas the area would be two thirds the product of length and width. If not they would have to be estimated by substituting a rectangle or a number of rectangles for them.
In the same way the addition and subtraction of pure numbers may also be carried out. We. need only represent the numbers by the ratios of the lengths of straight lines to a certain fixed line. The ratio of the length of the sum of the lines to the length of the fixed lines is equal to the sum of the numbers. The construction also applies to positive and negative numbers, if we represent them by the ratio of the length of straight lines of opposite directions to the length of a fixed line.
In order to multiply a given quantity by a given number, let the number be given as the ratio of the lengths of two straight lines . If the quantity is also represented by a straight line, all we have to do is to find a straight line whose length is to the length of as to . This can be done in many ways by
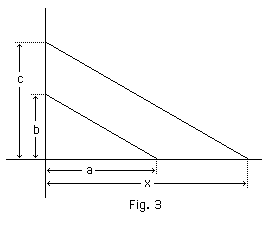
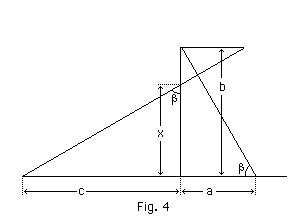
constructing any triangle with two sides equal to and and drawing a similar triangle with the side that corresponds to made equal to . As a rule it is convenient to draw and at right angles and the similar triangle either with its hypotenuse parallel (Fig. 3) or at right angles (Fig. 4) to the hypotenuse of the first triangle. Division by a given number is effected by the same construction; for the multiplication by the ratio alb -is equivalent to the divisions by the ratio .
If a, b, c are any given numbers, we can represent them by the ratios of three straight lines to a fixed line. Then the ratio of the line constructed in the way shown in Fig. 3 and Fig. 4 to the fixed line is equal to the number
Multiplication and division are in this way carried out simultaneously. In order to have multiplication alone, we need only make b equal 1 and in order to have division alone, we need only make or equal 1.
In order to include the multiplication and division of positive and negative numbers we can proceed in the following way. Let the lines corresponding to , Fig. 3, be drawn to the right side of the vertex to signify positive numbers and to the left side to signify negative numbers. Similarly let the lines corresponding to be drawn upward to signify positive numbers and downward to signify negative numbers. Then the drawing of a parallel to the hypotenuse of the rectangular triangle through the end of the line corresponding to c will always lead to the number
whatever the signs of may be.
The same definition will not hold for the construction of Fig. 4. If the positive direction of the line corresponding to is to the right and the positive direction of the line corresponding to is upwards then the positive directions of and ought to be such that when the right-angled triangle is turned through an angle of 90° to make the positive direction of coincident with the positive direction of , the positive direction of , coincides with the positive direction of . If we wish to have the positive direction of upward, the positive direction of would have to be to the left, or if we wish to have the positive direction of to the right, the positive direction of would have to be downward. If this is adhered to, the construction for division and multiplication will include the signs.
Last Updated August 2007