Heinrich Tietze on Numbers
Heinrich Tietze lectured on mathematics to students at the University of Munich who were studying a wide variety of different subjects. These students came from every faculty of the University. Tietze's aim was to talk about those mathematical topics which would convey the beauty of the subject, but at the same time required little background (as most of the students had very mathematical knowledge).
Below is a version of the first part of a lecture he gave on Numbers and Counting. This lecture formed the basis for a chapter in his book Gelöste und ungelöste mathematische Probleme aus alter und neuer Zeit which appeared in English translation as Famous Problems of Mathematics: Solved and Unsolved Mathematical Problems from Antiquity to Modern Times (1965).
Below is a version of the first part of a lecture he gave on Numbers and Counting. This lecture formed the basis for a chapter in his book Gelöste und ungelöste mathematische Probleme aus alter und neuer Zeit which appeared in English translation as Famous Problems of Mathematics: Solved and Unsolved Mathematical Problems from Antiquity to Modern Times (1965).
NUMBERS AND COUNTING
In how many ways would our culture be different than it is, if man had six fingers on each hand instead of five? Manufacturing and handicraft, of course, are fields which are strongly influenced by the number of fingers, and other fields whose historical development has been critically or marginally influenced by the number of our fingers come to mind. But nowhere has the influence of our ten fingers been so primary, as on the first beginnings of mathematics, that is, on the theory of numbers. In primitive societies the ten fingers of man comprised a counting and calculating apparatus he carried with him wherever he went. Because of this counting machine, the numbers from one to ten each received a special name. But the usefulness of this machine was limited. If the number of objects to be counted, such as the sheep in a herd, exceeded ten, the fingers of both hands were soon used up. The solution to this problem is clearly reflected in the nomenclature of numbers. The name fourteen, for example, means that there are four objects more than the number of all the fingers.
It may of course happen that all the fingers are used twice but objects to be counted still remain. Thus, twice the total count of fingers and six objects more is called twenty-six, twenty signifying twice ten, twice the full count of all the fingers.
The names of the numbers: one, two, three, ten, twenty, thirty, ... are different, of course, in the various languages. Number symbols (see Arabic_numerals, Babylonian_numerals, Egyptian_numerals, Greek_numbers, Indian_numerals, Mayan_mathematics) have also differed widely. Those we are accustomed to, which we call Arabic numerals, came into use relatively late in history. In primitive ages, before the invention of writing, there were names for numbers but no number symbols. Without referring to any particular number symbols, or any particular language, let us see how an extended counting process can be carried out using only the ten fingers of man. In one South African tribe, it goes along smoothly in the following manner.
Let us suppose that a chieftain wishes to count a large number of men. As they pass before him, an aide raises one finger for the first, another for the next, and so on, so long as he has a finger available. This purely mechanical process does not require speaking a word or making a mark. But when ten people have passed, the counting capacity of this aide is gone. In order to continue the count - as before, without uttering a sound or making a mark - a second aide must take up the job. To show that the first aide - who counted the units - is finished with the range of numbers represented by his fingers, the second aide raises a finger while the first lowers both hands. One finger of the second aide is equivalent to all ten of the first aide. In our words, the second aide counts the tens. Now when another man of the group to be counted comes along - we would say the eleventh - the first aide begins again, raising one finger for each man who passes. After fourteen men have passed, the second aide has one finger raised, while the first holds up four. Because this process is carried out without speaking or writing, but only with the counting apparatus which man carries with him on his two hands, we see that our system of units and tens derives from our own bodies. After twenty - that is after ten and again ten - men have filed past, the first aide will again have all his fingers raised, and his counting capacity will again be exhausted. This will cause the second aide to raise his second finger as the first lowers his hands. The two raised fingers of the second aide represent as many counted men as twice the full finger count of the first aide. After ten times ten - in our words a hundred - have passed, the first aide will have exhausted his fingers for the tenth time, and the second aide will have raised his tenth finger, thus reaching the end of his counting capacity. A third aide will now be required. He will raise one finger to signify that the second aide has exhausted his counting capacity, while the second aide lowers all his. The fact that a hundred persons have passed before the Chief is symbolized by the picture of the first two aides standing with lowered hands, while the third - who counts the hundreds - has one finger raised. Now the first and second aide can start counting all over again, and only when they have reached the end of their counting capacity, i.e., when two hundred persons have passed, does the third aide raise his second finger. The three aides are sufficient for a count up to 1000; a fourth is needed to count between 1000 and 10000, etc. With each additional aide the range of numbers that can be counted is multiplied by ten. With seven aides one can count up to 10 million, with 8 up to 100 million. A population of 60 million, for instance, can be counted with 8 aides; 10 aides are sufficient to count all mankind.
In addition to the need for a counting procedure, there is the need for communicating it, either in writing or orally. Oral communication requires a word for each unit represented by a raised finger; in our language, there are special words for one, two, three, four, five, six, seven, eight, nine, ten, for ten times ten, or hundred, and for the numbers which result from multiplication by ten: thousand, million and billion.
To communicate by writing, we need symbols only for the numbers one to nine, in the form conventional to us:
1, 2, 3, 4, 5, 6, 7, 8, 9,
and one more symbol, zero:
0.
The symbol 10 signifies that the second aide has one finger raised, while the first has his hands lowered; [This shows how our written symbols were decisively influenced by the number of our fingers: 10 signifies that the counting capacity of the first aide has been exhausted once.] 14, that the second aide has one finger up and the first one four; and 472, that the third aide has four, the second seven and the first two fingers raised. In short, this manner of writing numbers, which has come down to us from India through the Arabs, known as the decimal system, is the exact systematic representation of the primitive South African counting process.
The pre-historic and historical development of this system was not uniform, but rather irregular. There are numerous examples of early deficiencies in the system: In written symbols, a deficiency is most marked in the case of the Romans, who, lacking a zero, could not discover any position system. They required not only new words for 100 or 1000, but also new symbols: C, M (in addition to the ten-fold multiples of 5: V = 5, L = 50, D = 500).
[Through habitual usage, a special symbol for zero is taken as a matter of course, although the young child may still view it as something special. But in the development of mathematics, it took a special insight to understand that a positional notation was impossible without a symbol for the unoccupied positions. The Indian mathematician Brahmagupta developed rules for computing with zero, whose significance for the positional system seems to have been known at the time.]
Various modern languages still show evidences of such deficiencies. In French, quatre-vingt and quatre-vingt-dix are deviations from the decimal constructions; quatre-vingt means 4 times 20, not 8 times 10. In many languages the count above ten does not proceed with formations such as ten and one, ten and two, but with special words:
elf, onze, eleven;
zwölf, douze, twelve;
as if ten was not yet considered a separate and larger unit than the first nine digits; it is only with dreizehn in German or thirteen in English that the decimal construction becomes manifest.
zwölf, douze, twelve;
How, then, would the number system have developed if men had 12 rather than 10 fingers? Our African chieftain would have needed a new aide only after 12 men had been counted; and a third, only when the counting capacity of the second had been exhausted, which would now be a little later, because of the 12-fingered hands of the first two aides; a third aide would now be needed only after the second had held up all of his 12 fingers, that is after the first had raised all of his 12 fingers 12 times. The third aide would be needed beginning with the number which we call one-hundred forty-four and write 144. Three aides would be enough to count up to twelve times twelve times twelve (1728, using our designation), and only after this would a fourth aide be needed.
The names and symbols for numbers would of course also be quite different from those in present use. For example, consider the number for which we write 15 and say fifteen. Using the twelve-fingered aides in the counting process detailed above, the second aide will have one finger raised, and the first, three. To name this number we would not then say ten and five or fifteen, but perhaps twelve-three. The written system would differ correspondingly. Since the first aide has three fingers raised and the second aide one, we would now write 13 in the twelve-fingered system instead of 15, as in the decimal system. We shall use bold face for the duodecimal notation to distinguish it from the decimal system.
The duodecimal system may seem strange at first, but more detailed examination will make it more familiar. To begin with, we need a word for each of the finger patterns exhibited by the first aide (the units from one to twelve). We can use the usual words one to nine for the patterns starting with one finger of one hand (1 + 0), two fingers of one hand (2 + 0), up to the pattern with six fingers of one hand and three fingers of the second hand (6 + 3); but, in order to avoid confusion with the decimal system, we shall introduce new names for the patterns (6 + 4, 6 + 5, and 6 + 6) in place of the customary ten, eleven, and twelve. Our choice of names for these last three can be made arbitrarily, since the origin of the customary number names: one, two, ... , nine, ten is so old that it is lost, and therefore we cannot know what the words would have been, had man been born with twelve fingers. [0ne would have to consider how the consequent change in manual skill would have influenced the whole history of tools and weapons and the division of peoples according to their linguistic roots; if not indeed a whole new world.] For convenience, we shall use the word 'year' for twelve and shall borrow the tenth and eleventh letters of the Greek alphabet, kappa (k) and lambda (l), for the patterns with six fingers of one hand and four of the second hand (6 + 4), and six fingers of one hand and five of the second hand (6 + 5), respectively. In this way, we shall later be able to use k and l as number symbols instead of 10 and 11. However, to avoid awkwardness, we will sometimes use the familiar words: ten, eleven, and twelve.
We can now assign names to the numbers greater than twelve (= year) in the duodecimal system. Thirteen is now twelve plus one and we will refer to it as twelve-one or year-one. Continuing in this way, we would have
twelve-two = year-two (fourteen),
twelve-three = year three (fifteen),
twelve-four = year-four (sixteen),
......
twelve-nine = year-nine (twenty-one),
twelve-ten = year-kappa (twenty-two),
twelve-eleven = year-lambda (twenty-three).
The next number would be two times twelve = two times year (twenty-four), the number of months in two years. Continuing, we get two times twelve and one (twenty-five) up to eleven times twelve = lambda times year (one hundred and thirty-two), and then eleven times twelve and one, eleven times twelve and two, etc. until finally we reach eleven times twelve and eleven = lambda times year and lambda (one hundred forty-three). We would now need a new word for year times year or twelve times twelve (hundred forty-four). We might use year-squared or twelve-squared, just as we use the word hundred for ten times ten in the decimal system. This corresponds to the point in the counting process at which the first twelve-fingered aide has raised and lowered all his fingers twelve times, the second aide has raised his twelve fingers in order and has lowered them, and the third aide has raised his first finger.
twelve-three = year three (fifteen),
twelve-four = year-four (sixteen),
......
twelve-nine = year-nine (twenty-one),
twelve-ten = year-kappa (twenty-two),
twelve-eleven = year-lambda (twenty-three).
But the symbolic representation of numbers would also change. For the numbers one through nine we will use the usual symbols, but now these will be printed in bold face to emphasize the fact that the duodecimal system is meant (bold face type will be used in this article for all symbols, except k and l, referring to the duodecimal system). In addition, we introduce special symbols T and E, or k and l, for ten and eleven. The first two are meant to be reminiscent of the words ten and eleven, the last two of the words kappa and lambda, which we have chosen as names for these numbers. We would then have the following symbols (besides the symbol 0 for zero):
1, 2, 3, 4, 5, 6, 7, 8, 9, T (or k), E (or l).
What shall we write for twelve = year? Since this is the number at which the first aide (who counts the units) lowers all his fingers, while the second (who counts the years) raises one, it would be logical to write 10 (= a full year and no months). We would then have the following new notation:
twelve = year (12) is now 10
twelve-one = year-one (13) is now 11
twelve-two = year-two (14) is now 12
twelve-three = year-three (15) is now 13
.........................................
twelve-nine = year-nine (21) is now 19
twelve-ten = year-kappa (22) is now 1T (or 1k)
twelve-eleven = year-lambda (23) is now 1E (or 1l)
two × twelve = two × year (24) is now 20
two × twelve and one (25) is now 21
etc.
Continuing, we reach:
twelve-one = year-one (13) is now 11
twelve-two = year-two (14) is now 12
twelve-three = year-three (15) is now 13
.........................................
twelve-nine = year-nine (21) is now 19
twelve-ten = year-kappa (22) is now 1T (or 1k)
twelve-eleven = year-lambda (23) is now 1E (or 1l)
two × twelve = two × year (24) is now 20
two × twelve and one (25) is now 21
etc.
nine × twelve and nine (117) now 99
nine × twelve and ten
= nine × year and kappa (118) now 9T (or 9k)
nine × twelve and eleven
= nine × year and lambda (119) now 9E (or 9l)
ten × twelve = kappa × year (120) now T0 (or k0)
ten × twelve and one (121) now T1 (or k1)
.........................................
ten × twelve and nine
= kappa × year and nine (129) now T9 (or k9)
ten × twelve and ten
= kappa × year and kappa (130) now TT (or kk)
ten × twelve and eleven
= kappa × year and lambda (131) now TE (or kl)
eleven × twelve
= lambda × year (132) now E0 (or l0)
eleven × twelve and one
= lambda × year and one (133) now E1 (or l1)
.........................................
eleven × twelve and nine
= lambda × year and nine (141) now E9 (or l9)
eleven × twelve and ten
= lambda × year and kappa (142) now ET (or lk)
eleven × twelve and eleven
= lambda × year and lambda (143) now EE (or ll),
and finally twelve × twelve = twelve squared:
twelve squared = year squared (144) now 100.
This corresponds to the case in which both the first and second twelve-fingered aides drop their hands while the third raises one finger.
nine × twelve and ten
= nine × year and kappa (118) now 9T (or 9k)
nine × twelve and eleven
= nine × year and lambda (119) now 9E (or 9l)
ten × twelve = kappa × year (120) now T0 (or k0)
ten × twelve and one (121) now T1 (or k1)
.........................................
ten × twelve and nine
= kappa × year and nine (129) now T9 (or k9)
ten × twelve and ten
= kappa × year and kappa (130) now TT (or kk)
ten × twelve and eleven
= kappa × year and lambda (131) now TE (or kl)
eleven × twelve
= lambda × year (132) now E0 (or l0)
eleven × twelve and one
= lambda × year and one (133) now E1 (or l1)
.........................................
eleven × twelve and nine
= lambda × year and nine (141) now E9 (or l9)
eleven × twelve and ten
= lambda × year and kappa (142) now ET (or lk)
eleven × twelve and eleven
= lambda × year and lambda (143) now EE (or ll),
and finally twelve × twelve = twelve squared:
twelve squared = year squared (144) now 100.
Force of habit, and our own hands, make us think that the decimal
| | | | | | | | | | | | | | | | | | | | | |
Fig. 1 Fig. 2
system is simple, compared to the strange and complicated duodecimal system. But the number ten - that is, the number itself (Fig. 1) and not the name or symbol representing it - has no intrinsic quality (except the anatomical one) to make it mathematically preferable to the number twelve (Fig. 2).
It should now be clear that any number could be substituted for 10 as a base in counting. We could, for instance, use the number nine. Our symbols would then be (using italics for nonary numbers)
1, 2, 3, 4, 5, 6, 7, 8, and 0.
The number nine would now be written as 10. Our ten would be understood as nine plus one, nine-one, and would be written 11, etc.;
our seventeen = nine + eight would be written 18,
our eighteen = twice nine would be written 20,
etc.
our eighty = eight times nine plus eight would be written 88,
our eighty-one = nine times nine would be written 100.
The latter is obvious because nine times nine (nine squared) is a new higher unit and thus plays the same role as ten times ten in the decimal system, or twelve times twelve in the duodecimal system.
The preceding discussion has nothing to do with the whole numbers themselves, but rather with their spoken and written symbols, that is, with the base 10 as a convention created by anatomy, an extra-mathematical consideration. There are essential mathematical properties of whole numbers, such as their relation to each other, which are independent of these formal conventions. Numbers have a meaning independent of their representation. The number shown in Fig. 1, for example, whether it is written as 10 in the decimal system, or as T in the duodecimal system or as 11 in the nonary system, is the number of the Commandments of the God of the Old Testament, the number of members (feet and wings) of a butterfly, a bee or a fly, and the number (responsible for our present numerical system) of fingers or toes of a man.
In the same way, the number in Fig. 2 is the number of disciples of Jesus, the number of months into which the year is divided, etc. It is the same number whether it is written as 12, or as 10, or as 13.
The arithmetical relations between numbers are also independent of their symbolic representations. The sum of the numbers shown in Figs. 1 and 2 is the number in Fig. 3.
| | | | | | | | | | | | | | | | | | | | | |
Fig. 3
In the decimal system, the sum is called twenty-two (22); in the duodecimal system, it is called twelve-ten or year-kappa (1T or 1k); in the nonary system, it is called twice nine plus four (24). The fact that the number of Fig. 3 is the sum of the numbers of Figs. 1 and 2 is independent of the particular representation chosen, but the symbols used to describe the addition depend on the choice of a base. Thus,
in the decimal system: 10 + 12 = 22,
in the duodecimal system: T + 10 = 1T (or k + 10 = 1k),
in the nonary system: 11 + 13 = 24. In Roman numerals, the addition would be written
X + XII = XXII.
Another essential property of a number, independent of its designation, is that of being a square, that is the product of a number by itself: e.g. twenty-five = five times five = five squared. The reason is that the statement "N is a square" merely means that there is a square which can be partitioned into N subsquares in the way shown in Figs. 4, 5, and 6
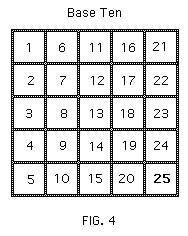
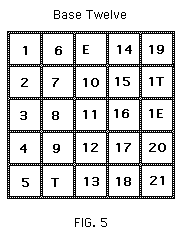
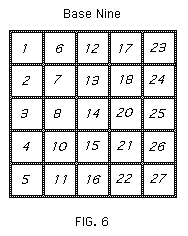
for N twenty-five. Whether the subsquares are numbered relative to the decimal system (Fig. 4), or the duodecimal system (Fig. 5), or the nonary system (Fig. 6) has no bearing on the fact that the number of subsquares is a square number.
The property of being either a composite number or a prime is also an essential property. On the other hand, a "round" number, a number which ends in one or more zeros, is clearly dependent on the choice of base. The celebration of a 70th or 80th birthday, or a 50th wedding anniversary, the designation of centuries as historical units of comparison, are also tied to a system based on the number ten. In the duodecimal system, entirely different numbers, those divisible by 12, would be "round."
We have dwelt on the role of the number ten in our numerical system to show that ten has no essential mathematical properties which make it basic to counting, but that on the contrary any other positive whole number (greater than one) would do just as well. What is decisive, is the positional principle on which all our representational systems rest, no matter what the base. This positional principle represents an arbitrary number by digits, each of which is assigned a positional value; a special symbol, our zero, is required for the positions not occupied by digits.
The reader has probably already asked himself where the mathematical problem is in all this? In ancient times or among primitive peoples, the development of a systematic method of counting and of representing numbers was in fact a problem of great cultural importance, whether or not it was consciously posed. Methods of counting were evolved gradually, by no one man. They culminated in the positional principle and in the choice of a base, which made it possible to represent any number, no matter how large, with a limited number of symbols (digits). This systematic representation of numbers is intimately linked with the perception - already developed by Archimedes in his grains of sand theory - that the sequence of numbers 1, 2, 3, - - - is infinite. The difficulty in evolving the positional system (which children now take for granted) is best illustrated by the history of zero, i.e. the introduction of a symbol for an unoccupied position - a symbol which, as we know, the Romans lacked. To grasp the progress represented by the decimal system and its positional system (which gradually spread over Europe only after the year 1000), consider the problem of conducting all our monetary, insurance, statistical and other numerical affairs in Roman numerals. Compare the time required to do a simple problem in addition in the decimal system with that required by the same problem using Roman numerals:
146 CXLVI 1993 MCMXCII 500 D 204 CCIV 59 LIX 140 CXL 98 XCVIII 301 CCCI ---- -------- 3441 MMMCDXLI
It would not, then, make a great deal of difference to counting and calculating if man had been born with six fingers on each hand. It is not the preference accorded the number ten which matters, but rather the creation of a positional system for representing numbers, which is of decisive significance for our culture.
The origin of whole numbers in the counting process was the first mathematical activity of man. In addition, as long ago as the Babylonians and the Egyptians, man already knew fractions. A developed arithmetic dating back to 2000 B.C., with addition, subtraction, multiplication and division of fractions, was found in the Rhind papyrus. Later, the domain of numbers was extended in three ways, but each extension had to overcome many obstacles. The three generalizations which successively broadened the concept of number were those of negative, irrational, and finally of imaginary numbers.
If one follows the vicissitudes suffered by these numbers before they gained full maturity and recognition, one finds in each case the same childhood diseases and the same adolescent difficulties in the transition to a ripe, fully developed theory, First, there were tentative trials of the new numbers, whose foundations were uncertain; then a growing familiarity with them on the one hand, and a distinct aversion towards them on the other - if indeed their existence was recognized at all; at the same time a defence of the new acquisition, often on faulty grounds, was carried on by its champions.
Those who remember their own introduction to negative, then irrational and perhaps imaginary numbers, will agree that the stages in their learning process were analogous to those of the historical development of the subject and that the process is comparable to the well-known biological principle: ontogeny recapitulates phylogeny. We will not discuss classroom reminiscences of imaginary numbers, even though these numbers are very important in the development of other branches of mathematics. We must certainly recall our own resistance to the rule for multiplying negative numbers: -1 × -1 = +1 (minus times minus equals plus). As for the irrational numbers, the high schools are forced to forego teaching them on a really rigorous basis, because this is much too difficult. High schools have to try to get by as cheaply as possible without making the gifted students feel that they are being stuffed with material merely because it is prescribed, and hence to become disenchanted with the subject because of its apparent lack of rigour.
A major difficulty in understanding the new kinds of numbers - as evidenced both by their historical development and the learning process of the student - is the fact that their main function is no longer that of counting, but of measuring. Both fractions and negative numbers, however, do not lose their counting function completely. If I take several apples, about equal in size, and cut each of them into three parts, and then take five of these parts, the fraction 5 /3 still involves counting in the sense that 5 is a numerator or numberer. However, the part has replaced the whole as a unit. Negative numbers are used with positive ones in counting outgo and intake, so that commercial arithmetic has played a substantial role in the extension of the number domain. But the fraction 5 /3 can also be interpreted as the measurement of a length (by dividing the length into three equal parts and then considering five such parts side by side). Negative and positive numbers can also be used to measure lengths by taking a fixed point on a line and specifying that measurements to the right of the point are positive and to the left negative. An example is the temperature scale of a thermometer.
Before discussing the measuring functions of fractions and negative numbers any further, we must consider irrational numbers. A rigorous foundation for these numbers was not developed until the latter part of the 19th century, although their origin goes back to classical antiquity. Although we cannot fully treat the subject of irrational numbers here, we can indicate the nature of the problem solved by the introduction of irrational numbers.
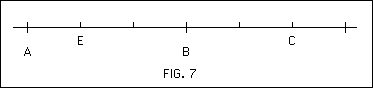
Consider Fig. 7, in which is the unit of length and the length of is 5 /3 . Consequently, 1 /5 of is equal to 1 /3 of , that is as 5 : 3. Hence, the two segments are in the ratio of two whole numbers. In other words, and have a common measure, (of which they are both multiples). Therefore, and are said to be commensurable.
The Greeks perceived that there are segments which are not in the ratio of two whole numbers, and therefore have no common measure or are incommensurable. The most familiar example is the one given by Euclid in the 10th book of his Elements (Fig. 8).
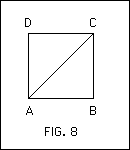
The diagonal and the side of the square are incommensurable, since the contrary assumption leads to a contradiction. For if and have a common measure, it is a segment which can be marked off exactly times on and times on , with and suitable positive whole numbers; then the th part of is equal to the th part of and as . It can be shown that this implies that
.
Further, it can be proved that whole numbers and cannot satisfy this equation. Hence there cannot be two whole numbers and such that and are in the ratio .
[We can cheek this by carefully measuring the side and diagonal of a square. If is divided into 1000 parts, measurement of will yield 1414 of these parts so that is as 1414 : 1000, or 707 : 500. But, if = 707, and = 500,
and
,
so that and are only approximately, but not exactly equal, as they must be if is to be the exact ratio of the diagonal to the side of a square.
One must thoroughly understand that the spirit of classical Greek mathematics was based on exactitude and went far beyond the practical considerations of surveying. Therefore a sharp distinction must be made between approximate, and absolutely exact relationships. Only a rigorously exact mathematics could make the distinction between commensurable and incommensurable segments - a distinction which would make no sense in practical measurements.]
Therefore, if is the unit of length, the length of the segment cannot be represented by any fraction . Nevertheless, the need to assign numbers to the ratios of any two segments (commensurable or not) grew more and more imperative. This could be done only by extending the domain of fractions (rational numbers) by introducing new numbers-those we. call irrational.
Greek mathematics could compare two segments as equal (or larger or smaller); what it lacked was the concept of assigning numbers to lengths of segments incommensurable with a prescribed unit segment. While now we can simply say: If the side is the unit of length, the length of the diagonal is equal to √2, this would have been impossible for the Greeks because √2 does not exist in the domain of rational numbers.
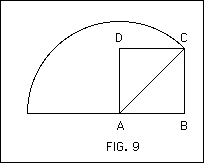
Another example is the problem of adding to AB (Fig. 9). We can write the sum as 1 + √2; the Greeks could add the two segments geometrically, but could not add them arithmetically.
The extension of the number system was required not only for geometric measurements, but also for the solution of algebraic equations. As a result, beginning with the Arab mathematicians, the use of irrational numbers spread after 1000 A.D. It was Michael Stifel (1487-1567) who gave them the name of irrational numbers. But it was not until the 19th century that rigorous theories of irrational numbers were developed. During the second half of the century, a period of critical activity and great discoveries, many leading mathematicians became interested in building a solid foundation for mathematics. Various theories of irrational numbers were evolved; among them the theory of Dedekind, which since then has been preferred by an ever growing number of mathematicians. Dedekind's theory of irrational numbers is too technical for discussion here, but we do want to say a few words about this great thinker.
Whoever is willing to agree that the outlook of all branches of mathematics is essentially determined by the ideas of outstanding investigators and the new concepts introduced by them, must recognize in Dedekind one of those creative spirits who have given modern mathematics its characteristic stamp. Dedekind's work (the theory of ideals) was in a field in which Gauss had been a pioneer; it was algebraic in origin and dealt among other things with problems of factorization analogous to the familiar problem of factoring a number into its prime factors, e.g.: 84 = 2.2.3.7. Kummer (1810-1893) had already illuminated part of this field. Dedekind's theory went on to embrace the whole field and was so profound that it determined the development not only of algebra but of other branches of mathematics, and will no doubt continue to do so for a long time.
Dedekind's achievements had to do not with calculating but with the analysis of concepts, which made it difficult at the beginning for his contemporaries to enter into his new conceptual world. This was true even in the case of the theory of irrational numbers. Added to this barrier was the fact that the need for such a rigorous, systematic treatment of irrational numbers, first recognized by Dedekind, was by no means generally realized. He explained this need in 1858, in a lecture given while he was a Professor at Zurich. By late autumn of that same year he had evolved a systematic theory, but it was not until 1872 that he published it, under the stimulus of the appearance of other theories of irrational numbers. Even then the new concepts were slow to influence the foundations of arithmetic and were still rejected by many.
Significant changes in mathematics and the great impetus they gave to new surges of development were conceived by a man whose outer life was so uneventful that it can be recounted in a few lines.
Richard Dedekind was born in Brunswick (the birthplace of the great Gauss), 6 October 1831, where he lived until he was 19. After twelve years of study and teaching elsewhere, he returned to stay until his death in his 85th year. In 1850 he went to continue his studies, which he had begun at the Collegium Carolinum in 1848, in Göttingen. He received his doctorate from Göttingen in 1852 and in 1854 became a lecturer. In 1858 he was made Professor at the Federal Institute of Technology at Zurich, and in 1862 was called to the Technische Hochschule in Brunswick.
For many years Dedekind was the only surviving student of Gauss. At 19 he had heard Gauss lecture in the small auditorium of the Göttingen Observatory. While at Göttingen, Dedekind was a colleague and friend of Bernhard Riemann. Thus, for a decade and a half, Dedekind served as a living bond between the creative minds of the new century and the great men who had preceded him. But for a long time, the importance of Dedekind's work was not recognized. In 1904, an academic calendar appeared, with the motto "nulla dies nisi festiva," which gave the birth or death date of a mathematician for each day of the year. On it, 4 September 1899 was marked as the day of Dedekind's death. Dedekind wrote to the publisher that 4 September might be correct but 1899 certainly was not. He had spent the day, he volunteered, in the best of health and in a very stimulating discussion with his dinner guest and honoured friend, Georg Cantor of Halle, who, Dedekind added, had used this opportunity to deal a death blow not to his friend, but to an error he had made. On 12 February 1916, his peaceful, academic life closed. Dedekind had lived to see his long unrecognized ideas gain acceptance, and begin to be accorded their true importance in mathematics.
Dedekind's theory of irrational numbers gained wider and wider acceptance over other theories because, although it appears strange and abstract to the beginner, most mathematicians agree that it most nearly approaches the essence of the matter.
You may be surprised to learn that several theories on a given subject, e.g. irrational numbers, may exist side by side, and that to some extent the choice of any one is a matter of individual taste. For example, there is a theory that before their separation by the Atlantic Ocean the Eastern and Western hemispheres were joined, and there is a second theory which maintains the opposite. One theory may sooner or later be proved incorrect, but meanwhile both are tenable. In the case of the irrational numbers, it is possible to have several equally valid theories, because their validity depends on consistency and not on empirical observation.
Last Updated April 2007