Topology and Scottish mathematical physics
The Scottish mathematical physicists referred to in the title are Thomson, Maxwell and Tait. These three became involved in topological concepts, in particular knot theory, because it entered their physical considerations in a natural way. In 1847 Listing published Vorstudien zur Topologie Ⓣ and then Riemann published important papers on complex analysis in 1851 and 1857 which investigated connectivity and Riemann surfaces. The Scottish mathematical physicists did not know of these papers until much later but Helmholtz, whose paper of 1858 directly influenced them, built much on Riemann's ideas.
In 1858 Helmholtz published his important paper in Crelle's Journal on the motion of a perfect fluid. Helmholtz's paper Uber Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen Ⓣ began by decomposing the motion of a perfect fluid into translation, rotation and deformation. It was this aspect which first interested Tait who saw that by using Hamilton's quaternions he could express the fluid velocity as a "vector function". However the ideas in the paper which eventually led the Scottish mathematical physicists to topological considerations concerned vortex lines and vortex tubes. Helmholtz defined vortex lines as lines coinciding with the local direction of the axis of rotation of the fluid, and vortex tubes as bundles of vortex lines through an infinitesimal element of area. Helmholtz showed that the vortex tubes had to close up and also that the particles in a vortex tube at any given instant would remain in the tube indefinitely so no matter how much the tube was distorted it would retain its shape.
Helmholtz was aware of the topological ideas in his paper, particularly the fact that the region outside a vortex tube was multiply connected which led him to consider many-valued potential functions. He described his theoretical conclusions regarding two circular vortex rings with a common axis of symmetry in the following way:-
Tait began to think about knots and Thomson's second paper on vortex atoms, which appeared in 1869, included diagram of knots and links drawn by Tait. Long before this, however, Maxwell had entered the discussions which went on in letters exchanged by the three Scottish mathematical physicists. He was interested in knots because of electromagnetic considerations and in a letter to Tait written on the 4 December 1867 he rediscovered an integral formula counting the linking number of two closed curves which Gauss had discovered, but had not published, in 1833. Maxwell also gave equations in three dimensions which represented knotted curves.
However just when their work was proceeding rapidly, a major problem arose. Bertrand claimed that Helmholtz's 1858 paper, on which the idea of vortex atoms was based, was wrong. Maxwell was already intrigued by the problems and was not convinced that Bertrand's objections dealt a serious blow to Helmholtz's paper. In September 1868 Maxwell wrote several manuscripts which study knots and links. He set out the basic problem of the classification of knots and links as follows:-
He then looked at ways of modifying the diagrams without changing the link or knot. For a region bounded by one arc Maxwell noted that the region could be eliminated by uncoiling the curve. For regions bounded by two arcs, he noted that there were two cases, one where the arcs could be separated and the region eliminated, the other where this could not be done without making changes in other parts of the diagram. For regions bounded by three arcs Maxwell noted that again there were two cases:-
In a a second manuscript Maxwell considered a region of space bounded by one external surface of genus and internal surfaces of genus and showed that the region possessed cycles and was -ly connected. Now in modern terminology Maxwell was claiming that the first Betti number of the region was . Again we should note that Maxwell did not give precise mathematical definitions of the concepts he was dealing with so no rigorous proof was possible. It is reasonable to ask how he then found the correct answer. The reason was that Maxwell, and for that matter Thomson too, reached their correct results using correct physical understanding, rather than mathematical intuition.
These manuscripts by Maxwell were not published at the time they were written despite Tait asking him to submit his ideas on knot theory to the Royal Society of Edinburgh for publication. However, more than 100 years after they were written these manuscripts were published in [2]. There are three manuscripts on knots and some time between the second, which Maxwell wrote in October 1868, and the third, which he wrote on 29 December 1868, he had read Listing's 1847 paper Vorstudien zur Topologie Ⓣ for in the third manuscript he lists Listing's main results. In February 1869 Maxwell presented an account of Listing's topological ideas to the London Mathematical Society.
In 1869 Thomson tried to clarify the topological ideas that he was using. The problem really came down to the fact that, perhaps not surprisingly, he had confused what we know today are two different concepts. He wrote:-
By 1876 Thomson had made little progress with his ideas of vortex atoms. There were many problems in his way and indeed by this stage he had not succeeded in mathematically describing how two vortex rings would interact if they did not have a common axis of symmetry much more the way that knotted vortices would interact. Also there was no insight into vortex atoms through lists of knots which, in Thomson's theory, would explain the chemical elements. Tait decided to embark on a classification of plane closed curves in 1876, writing in a report to the British Association for the Advancement of Science:-
There were then two basic problems to solve. Firstly which sequences of the above type correspond to a knot, and secondly how could it be determined when two knots described by such sequences were the same. However there were some other problems, for example although a sequence of length 10, say, might represent a knot it might be one with less than 5 crossings. It might be a knot which could be reduced to one with fewer crossings. For example if the projection contained a crossing which divided the curve into two parts which did not intersect, then this was a nugatory crossing which could be removed by a twist.
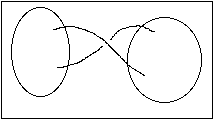
Tait conjectured that an alternating diagram without nugatory crossings would contain the minimum number of crossings. This became known as Tait's first conjecture. He gave a "proof" which showed that only nugatory crossings allowed the number of crossings to be reduced. However this is not good enough for there might be a sequence of moves which first increase the number of crossings, then further moves reduce to a fewer number of crossings than were there originally. If we interpret Tait in a form that he seems to have used the conjecture, namely that two alternating diagrams without nugatory crossings representing the same prime knot are related by a sequence of twists, then we get what has been called Tait's second conjecture. This was not finally proved until 1993.
Without any rigorous theory, which would have been well beyond nineteenth century mathematics, Tait began to classify knots using his mathematical and geometrical intuition. He knew that what was really required was a knot invariant, that is something which would be independent of the way that the knot was represented in two dimensions. First he looked for numerical invariants and considered the minimal number of crossings that a given knot might have in a two dimensional representation. This would lead him to Tait's first conjecture for alternating knots.
Another idea which seemed promising to Tait was the "beknottedness" which he defined as follows. Travel round the knot diagram and immediately after each crossing throw a copper coin to the left and a silver coin to the right if the crossing was above, or throw a silver coin to the left and a copper coin to the right if the crossing was below.
Tait then defined "beknottedness" (now known as the twist number) as the excess of silver crossings over copper ones. If only diagrams without nugatory crossings were considered then Tait believed that this was a knot invariant. In fact it is not, but for alternating knots, it is an invariant and this fact is a consequence of Tait's second conjecture (a theorem since 1993). He tried other more obviously physical ideas such as considering the knot as a circuit and looking at the work done by a magnetic particle carried by a current in the knot. He tried another idea which at first looked very promising to him, namely the minimal number of crossings which required to be changed for under to over (or visa-versa) to unknot the knot. His first thought was that this would be half the beknottedness. He soon saw that this was not so. Seeing that the two concepts were distinct Tait changed his definitions and called the minimal number of crossings which required to be changed to unknot the diagram the beknottedness and he called the minimal number of crossings the knottiness.
Listing had introduced polynomials in to variables associated with a knot. These were produced by marking the four corners of a crossing or (for left of right) according to a rule which again related to over of under crossings. These polynomials were not invariants, however. Tait tried a similar idea where he marked the regions of the graph or and then connected regions with a multiple bond of the order of the number of crossings on the boundary between the two regions. He was inspired to do this by analogy with chemical representations invented by his colleague (and brother-in-law) Alexander Crum Brown.
By 1877 Tait had classified all knots with seven crossings but he stopped there. He returned to the topic of knots in his address to the Edinburgh Mathematical Society in 1883:-
In 1858 Helmholtz published his important paper in Crelle's Journal on the motion of a perfect fluid. Helmholtz's paper Uber Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen Ⓣ began by decomposing the motion of a perfect fluid into translation, rotation and deformation. It was this aspect which first interested Tait who saw that by using Hamilton's quaternions he could express the fluid velocity as a "vector function". However the ideas in the paper which eventually led the Scottish mathematical physicists to topological considerations concerned vortex lines and vortex tubes. Helmholtz defined vortex lines as lines coinciding with the local direction of the axis of rotation of the fluid, and vortex tubes as bundles of vortex lines through an infinitesimal element of area. Helmholtz showed that the vortex tubes had to close up and also that the particles in a vortex tube at any given instant would remain in the tube indefinitely so no matter how much the tube was distorted it would retain its shape.
Helmholtz was aware of the topological ideas in his paper, particularly the fact that the region outside a vortex tube was multiply connected which led him to consider many-valued potential functions. He described his theoretical conclusions regarding two circular vortex rings with a common axis of symmetry in the following way:-
If they both have the same direction of rotation they will proceed in the same sense, and the ring in front will enlarge itself and move slower, while the second one will shrink and move faster, if the velocities of translation are not too different, the second will finally reach the first and pass through it. Then the same game will be repeated with the other ring, so the ring will pass alternately one through the other.As we have mentioned Tait's first interest in Helmholtz' paper was because he saw applications of quaternions there. It was not until 1867 that Tait verified Helmholtz' theoretical claims regarding two circular vortex rings with experiments with smoke rings. He used two boxes each with a rubber diaphragm which shot out white smoke rings when the diaphragm was struck. Thomson wrote to Helmholtz on 22 January 1867:-
... a few days ago Tait showed me in Edinburgh a magnificent way of producing [vortex rings]. We sometimes can make one ring shoot through another, illustrating perfectly your description; when one ring passes near another, each is much disturbed, and is seen to be in a state of violent vibration for a few seconds, till it settles again into its circular form. ... The vibrations make a beautiful subject for mathematical work.These experiments were to have a major influence on Thomson who saw the permanence of form as a possible explanation for atoms and therefore explain the way that the different elements could be built. It is remarkable that Thomson was able to develop his ideas quickly enough that he could publish On vortex atoms in the Proceedings of the Royal Society of Edinburgh still in 1867. In this paper he wrote:-
Leucretius's atom does not explain any of the properties of matter without attributing them to the atom itself ... The possibility of founding a theory of elastic solids and liquids on the dynamics of closely packed vortex atoms may be reasonably anticipated.Although was now know that Thomson was completely wrong, there is much in the way of correct reasoning in the quote we have just given. It was an idea which also led to interesting mathematical questions. As he wrote in the same paper:-
A full mathematical investigation of the mutual action between two vortex rings of any given velocities passing one another in any two lines, so directed that they never come nearer to one one another than a large multiple of the diameter of either, is a perfect mathematical problem; and the novelty of the circumstances contemplated presents difficulties of an exciting character. Its solution will be the proposed new kinetic theory of gases.Thomson, as most scientists of his time, viewed space as being filled with a perfect fluid, the aether. The vortex atoms were then knotted tubes of aether which, by Helmholtz's theory, retained their form despite being distorted. This stability of vortices explained the stability of atoms. The vortex atoms, being built from the aether, required no special material. The different elements were accounted for by atoms composed of different knots or links and oscillations of the knots would, Thomson believed, explain the spectral lines which were characteristic of the different elements.
Tait began to think about knots and Thomson's second paper on vortex atoms, which appeared in 1869, included diagram of knots and links drawn by Tait. Long before this, however, Maxwell had entered the discussions which went on in letters exchanged by the three Scottish mathematical physicists. He was interested in knots because of electromagnetic considerations and in a letter to Tait written on the 4 December 1867 he rediscovered an integral formula counting the linking number of two closed curves which Gauss had discovered, but had not published, in 1833. Maxwell also gave equations in three dimensions which represented knotted curves.
However just when their work was proceeding rapidly, a major problem arose. Bertrand claimed that Helmholtz's 1858 paper, on which the idea of vortex atoms was based, was wrong. Maxwell was already intrigued by the problems and was not convinced that Bertrand's objections dealt a serious blow to Helmholtz's paper. In September 1868 Maxwell wrote several manuscripts which study knots and links. He set out the basic problem of the classification of knots and links as follows:-
Let any system of closed curves in space be given and let them be supposed capable of having their forms changed in any continuous manner, provided that no two curves or branches of a curve ever pass through the same point of space, we propose to investigate the necessary relations between the positions of the curves and the degree of complication of the different curves of the system.Maxwell considered two-dimensional projections of links and devised a way of coding the diagrams to indicate which curve was above and which below at crossings on the projections.
He then looked at ways of modifying the diagrams without changing the link or knot. For a region bounded by one arc Maxwell noted that the region could be eliminated by uncoiling the curve. For regions bounded by two arcs, he noted that there were two cases, one where the arcs could be separated and the region eliminated, the other where this could not be done without making changes in other parts of the diagram. For regions bounded by three arcs Maxwell noted that again there were two cases:-
In the first case any one curve can be moved past the intersection of the other two without disturbing them. In the second case this cannot be done and the intersection of two curves is a bar to the motion of the third in that direction.Although his approach contained no mathematical rigour, still it is interesting to note that at this early stage Maxwell had defined the "Reidemeister moves" which would be shown to be the fundamental moves in modifying knots in the 1920s.
In a a second manuscript Maxwell considered a region of space bounded by one external surface of genus and internal surfaces of genus and showed that the region possessed cycles and was -ly connected. Now in modern terminology Maxwell was claiming that the first Betti number of the region was . Again we should note that Maxwell did not give precise mathematical definitions of the concepts he was dealing with so no rigorous proof was possible. It is reasonable to ask how he then found the correct answer. The reason was that Maxwell, and for that matter Thomson too, reached their correct results using correct physical understanding, rather than mathematical intuition.
These manuscripts by Maxwell were not published at the time they were written despite Tait asking him to submit his ideas on knot theory to the Royal Society of Edinburgh for publication. However, more than 100 years after they were written these manuscripts were published in [2]. There are three manuscripts on knots and some time between the second, which Maxwell wrote in October 1868, and the third, which he wrote on 29 December 1868, he had read Listing's 1847 paper Vorstudien zur Topologie Ⓣ for in the third manuscript he lists Listing's main results. In February 1869 Maxwell presented an account of Listing's topological ideas to the London Mathematical Society.
In 1869 Thomson tried to clarify the topological ideas that he was using. The problem really came down to the fact that, perhaps not surprisingly, he had confused what we know today are two different concepts. He wrote:-
I shall call a finite portion of space n-ply continuous when its bounding surface is such that there are n irreconcilable paths between any two points on it.He explains that two irreconcilable paths between points and are paths which cannot be smoothly transformed into each other by paths which remain within the portion of space considered. This definition does not really work although one can see Thomson struggling to reach a definition of homotopy. He does not compose his paths, however, a vital ingredient in the definition of homotopy. In the proofs he gave in the paper Thomson does not even try to use his definition but rather resorts to arguments involving virtual barriers which would stop fluid flowing. Again his topology is driven by physical ideas of fluid flow but this notion, similar to the idea of a "cutting surface" which Riemann had introduced and Helmholtz had used, relates to our present day idea of homology, not homotopy.
By 1876 Thomson had made little progress with his ideas of vortex atoms. There were many problems in his way and indeed by this stage he had not succeeded in mathematically describing how two vortex rings would interact if they did not have a common axis of symmetry much more the way that knotted vortices would interact. Also there was no insight into vortex atoms through lists of knots which, in Thomson's theory, would explain the chemical elements. Tait decided to embark on a classification of plane closed curves in 1876, writing in a report to the British Association for the Advancement of Science:-
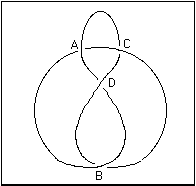
The development of this subject promises absolutely endless work - but work of a very interesting and useful kind - because it is intimately connected with the theory of knots, which (especially as applied in Sir W Thomson's Theory of Vortex Atoms) is likely soon to become an important branch of mathematics.Now by looking at plane closed curves Tait was considering alternating knots, namely those which when traversing the projection in 2-dimensional space the crossings go alternately over and under. Choosing a starting point and a direction to traverse the path, he labelled the first, third, fifth etc. points by etc. A knot with crossings would then be described by the sequence of crossings of length where each of occurred exactly twice when the knot was traversed. Tait called the sequence the "scheme of the knot".

A knot with scheme .
There were then two basic problems to solve. Firstly which sequences of the above type correspond to a knot, and secondly how could it be determined when two knots described by such sequences were the same. However there were some other problems, for example although a sequence of length 10, say, might represent a knot it might be one with less than 5 crossings. It might be a knot which could be reduced to one with fewer crossings. For example if the projection contained a crossing which divided the curve into two parts which did not intersect, then this was a nugatory crossing which could be removed by a twist.
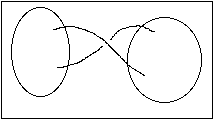
Example of a nugatory crossing.
Tait conjectured that an alternating diagram without nugatory crossings would contain the minimum number of crossings. This became known as Tait's first conjecture. He gave a "proof" which showed that only nugatory crossings allowed the number of crossings to be reduced. However this is not good enough for there might be a sequence of moves which first increase the number of crossings, then further moves reduce to a fewer number of crossings than were there originally. If we interpret Tait in a form that he seems to have used the conjecture, namely that two alternating diagrams without nugatory crossings representing the same prime knot are related by a sequence of twists, then we get what has been called Tait's second conjecture. This was not finally proved until 1993.
Without any rigorous theory, which would have been well beyond nineteenth century mathematics, Tait began to classify knots using his mathematical and geometrical intuition. He knew that what was really required was a knot invariant, that is something which would be independent of the way that the knot was represented in two dimensions. First he looked for numerical invariants and considered the minimal number of crossings that a given knot might have in a two dimensional representation. This would lead him to Tait's first conjecture for alternating knots.
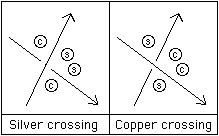
Another idea which seemed promising to Tait was the "beknottedness" which he defined as follows. Travel round the knot diagram and immediately after each crossing throw a copper coin to the left and a silver coin to the right if the crossing was above, or throw a silver coin to the left and a copper coin to the right if the crossing was below.

This led to:
Tait then defined "beknottedness" (now known as the twist number) as the excess of silver crossings over copper ones. If only diagrams without nugatory crossings were considered then Tait believed that this was a knot invariant. In fact it is not, but for alternating knots, it is an invariant and this fact is a consequence of Tait's second conjecture (a theorem since 1993). He tried other more obviously physical ideas such as considering the knot as a circuit and looking at the work done by a magnetic particle carried by a current in the knot. He tried another idea which at first looked very promising to him, namely the minimal number of crossings which required to be changed for under to over (or visa-versa) to unknot the knot. His first thought was that this would be half the beknottedness. He soon saw that this was not so. Seeing that the two concepts were distinct Tait changed his definitions and called the minimal number of crossings which required to be changed to unknot the diagram the beknottedness and he called the minimal number of crossings the knottiness.
Listing had introduced polynomials in to variables associated with a knot. These were produced by marking the four corners of a crossing or (for left of right) according to a rule which again related to over of under crossings. These polynomials were not invariants, however. Tait tried a similar idea where he marked the regions of the graph or and then connected regions with a multiple bond of the order of the number of crossings on the boundary between the two regions. He was inspired to do this by analogy with chemical representations invented by his colleague (and brother-in-law) Alexander Crum Brown.
By 1877 Tait had classified all knots with seven crossings but he stopped there. He returned to the topic of knots in his address to the Edinburgh Mathematical Society in 1883:-
We find that it becomes a mere question of skilled labour to draw all the possible knots having any assigned number of crossings. The requisite labour increases with extreme rapidity as the number of crossings is increased. ... I have not been able to find time to carry out this process further than the knots with seven crossings. ... It is greatly desired that someone, with the requisite leisure, should try to extend this list, if possible up to 11 ...Kirkman read the text of Tait's address and began to work on classifying knots with more than seven crossings. He sent Tait his results on knot projections with up to nine crossings in May 1884 but he had not looked at the problem of deciding which of the projections led to equivalent knots. Tait worked on this side of the problem and, considering only alternating knots, solved the equivalence problems within a few weeks. Tait seemed to know how to tell whether two knots were equivalent without rigorous methods. He states this quite clearly in the paper he wrote tabulating the knots where he says that his methods have:-
... the disadvantage of being to a greater or less extent tentative. Not that the rules laid down ... leave any room for mere guessing, but they are too complex to be always completely kept in view. Thus we cannot be absolutely certain that by means of such processes we have obtained all the essentially different forms which the definition we employ comprehends.Despite the problems Tait knew exactly what he was doing for, remarkably, his tables are correct. When Kirkman sent him all knot projections with 10 crossings in January 1885 again Tait found all in equivalent knots. The tables were printed in September 1885 and again they are completely correct. By then he had received from Kirkman 1581 knot projections with 11 crossings and this time Tait felt that he did not have the time to solve the equivalence problem for these. However by this time an American mathematician and engineer Charles N Little had sent Tait knot tables which he had calculated and Little began to extend the tables to knots other than alternating ones, and to knots with eleven crossings.
References (show)
- M Epple, Die Entstehung der Knotentheorie (Braunschweig, 1999).
- P M Harman (ed.), James Clerk Maxwell, The scientific letters and papers of James Clerk Maxwell 1862-1873 II (Cambridge, 1995).
- C G Knott, Life and Scientific Work of Peter Guthrie Tait (Cambridge, 1911).
- T Archibald, Connectivity and smoke-rings : Green's second identity in its first fifty years, Math. Mag. 62 (4) (1989), 219-232.
- M Epple, Topology, matter, and space. I. Topological notions in 19th-century natural philosophy, Arch. Hist. Exact Sci. 52 (4) (1998), 297-392.
- M Epple, Geometric aspects in the development of knot theory, in I M James (ed.), History of topology (Amsterdam, 1999), 301-358.
- C Nash, Topology and physics - a historical essay, in I M James (ed.), History of topology (Amsterdam, 1999), 359-416.
Written by J J O'Connor and E F Robertson
Last Update January 2001
Last Update January 2001