Squaring the circle
There are three classical problems in Greek mathematics which were extremely influential in the development of geometry. These problems were those of squaring the circle, doubling the cube and trisecting an angle. Although these are closely linked, we choose to examine them in separate articles. The present article studies what has become the most famous for these problems, namely the problem of squaring the circle or the quadrature of the circle as it is sometimes called.
One of the fascinations of this problem is that it has been of interest throughout the whole of the history of mathematics. From the oldest mathematical documents known up to the mathematics of today the problem and related problems concerning π have interested both professional mathematicians and amateur mathematicians.
One of the oldest surviving mathematical writings is the Rhind papyrus, named after the Scottish Egyptologist A Henry Rhind who purchased it in Luxor in 1858. It is a scroll about 6 metres long and of a metre wide and was written around 1650 BC by the scribe Ahmes who copied a document which is 200 years older. This gives date for the original papyrus of about 1850 BC but some experts believe that the Rhind papyrus is based on a work going back to 3400 BC.
In the Rhind papyrus Ahmes gives a rule to construct a square of area nearly equal to that of a circle. The rule is to cut off the circle's diameter and to construct a square on the remainder. Although this is not really a geometrical construction as such it does show that the problem of constructing a square of area equal to that of a circle goes back to the beginnings of mathematics. This is quite a good approximation, corresponding to a value of 3.1605, rather than 3.14159, for π.
The problem of squaring the circle in the form which we think of it today originated in Greek mathematics and it is not always properly understood. The problem was, given a circle, to construct geometrically a square equal in area to the given circle. The methods one was allowed to use to do this construction were not entirely clear, for really the range of methods used in geometry by the Greeks was enlarged through attempts to solve this and other classical problems. Pappus, writing in his work Mathematical collection at the end of the period of Greek development of geometry, distinguishes three types of methods used by the ancient Greeks (see for example [5]):-
The first mathematician who is on record as having attempted to square the circle is Anaxagoras. Plutarch, in his work On Exile which was written in the first century AD, says [4]:-
Oenopides is thought by Heath to be the person who required a plane solution to geometry problems. Proclus attributes two theorems to Oenopides , namely to draw a perpendicular to a line from a given point not on the line, and to construct from a given point on a given line, a line at a given angle to the given line. Heath believes that the significance of these elementary results was that Oenopides set out for the first time the explicit 'plane' or 'ruler and compass' type of construction. Heath writes [2]:-
Antiphon and Bryson both produced arguments relating to squaring the circle which were to prove important in the future development of mathematics. Antiphon inscribed a square in a circle, then a regular polygon with eight sides, then one with sixteen sides and he continued the process continually doubling the number of sides. It appears that Bryson improved the argument of Antiphon by not only inscribing polygons in a circle but also circumscribed polygons. Themistius states [1]:-
Hippias and Dinostratus are associated with the method of squaring the circle using a quadratrix. The curve it thought to be the invention of Hippias while its application to squaring the circle appears to be due to Dinostratus. The construction of this curve with a diagram is given in the biography of Hippias in this archive. Now this curve certainly solves the problem of squaring the circle but, as given by Hippias, the curve is constructed by mechanical means given by a uniform motion of a line in a time equal to the rotating radius of a circle. The construction was rightly criticised as requiring a knowledge of the ratio of a line and an arc of a circle, so one assumed as known the property required to square the circle in the first place. It is clear that Dinostratus never claimed that the quadratrix gave a plane method to square the circle. Nicomedes many years later also used the quadratrix to square the circle.
Aristotle did not seem to appreciate the contributions of those who had attempted to square the circle. He wrote in his work Physics :-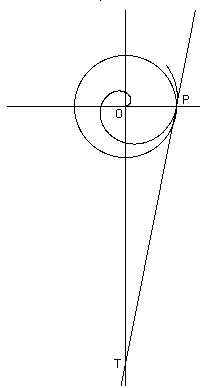
To square the circle Archimedes gives the following construction. Let be the point on the spiral when it has completed one turn. Let the tangent at cut the line perpendicular to at . Then Archimedes proves in Proposition 19 of On spirals that is the length of the circumference of the circle with radius . Now it may not be clear that this is solved the problem of squaring the circle but Archimedes had already proved as the first proposition of Measurement of the circle that the area of a circle is equal to a right-angled triangle having the two shorter sides equal to the radius of the circle and the circumference of the circle. So the area of the circle with radius is equal to the area of the triangle .
Both Apollonius and Carpus used curves to square the circle but it is not clear exactly what these curves were. The one used by Apollonius is called by Iamblichus 'sister of the cochloid' and this has led to various guesses as to what the curve might have been. Again the curve used by Carpus of Antioch is called the 'curve of double motion' which Paul Tannery argued was the cycloid.
Now we leave the ancient Greek period and look at later developments but the first comment we should make is that the Greeks were certainly not the only ones to be interested in squaring the circle at this time. Mathematicians in India were interested in the problem (see for example [11]) while in China mathematicians such as Liu Hsiao of the Han Dynasty showed himself to be one of the prominent of those attempting to square the circle in around 25 AD.
Some time later the Arab mathematicians were, like the Greeks, fascinated by the problem. In [6] the work of al-Haytham on squaring the circle is discussed. Now al-Haytham aimed to convince people that squaring the circle was possible by a plane construction but since his promised treatise on the topic never appeared he must at least have realised that he could not solve the problem.
Not long after the work of al-Haytham, Franco of Liège in 1050 wrote a treatise De quadratura circuli Ⓣ on squaring the circle. The text is reproduced in [8] and [9] and in it Franco examines three earlier methods based on the assumption that π is or 4. Franco states (reasonably enough) that these are false, then gives his own construction which is based on the assumption that π is . Although this treatise is of great historical interest, it does show how European mathematics at the time was far behind the ancient Greeks in depth of understanding.
Moving forward to about 1450, Cusa attempted to prove that the circle could be squared by a plane construction. Although his method of averaging certain inscribed and circumscribed polygons is quite fallacious, it is one of the first serious attempts in 'modern' Europe to solve the problem. Again it is worth commenting that the ancient Greeks basically knew that the circle could not be squared by plane methods, although they stood no chance of proving it. Regiomontanus, who brought a new impetus to European mathematics, was quick to point out the error in Cusa's arguments.
The mechanical methods of the Greeks certainly appealed to Leonardo who thought about mathematics in a very mechanical way. He devised several new mechanical methods to square the circle. Many mathematicians in the sixteenth century studied the problem, including Oronce Fine and Giambattista della Porta. The 'proof' by Fine was shown to be incorrect by Pedro Nunes soon after he produced it. The beginnings of the differential and integral calculus led to an increased interest in squaring the circle, but the new era of mathematics still produced fallacious 'proofs' of plane methods to square the circle. One such false proof, given by Saint-Vincent in a book published in 1647, was based on an early type of integration. The problem was still providing much impetus for mathematical development.
James Gregory developed a deep understanding of infinite sequences and convergence. He applied these ideas to the sequences of areas of the inscribed and circumscribed polygons of a circle and tried to use the method to prove that there was no plane construction for squaring the circle. His proof essentially attempted to prove that π was transcendental, that is not the root of a rational polynomial equation. Although he was correct in what he tried to prove, his proof was certainly not correct. However, others such as Huygens, believed that π was algebraic, that is that it is the root of a rational polynomial equation.
There was still an interest in obtaining methods to square the circle which were not plane methods. For example Johann Bernoulli gave a method of squaring the circle through the formation of evolvents and this method is described in detail in [12].
The historian of mathematics, Montucla, made squaring the circle the topic of his first historical work published in 1754. This was written at a time long before the problem was finally resolved, so is necessarily very outdated. The work is, however, a classic and still well worth reading.
A major step forward in proving that the circle could not be squared using ruler and compasses occurred in 1761 when Lambert proved that π was irrational. This was not enough to prove the impossibility of squaring the circle with ruler and compass since certain algebraic numbers can be constructed with ruler and compass. It only led to a greater flood of amateur solutions to the problem of squaring the circle and in 1775 the Paris Académie des Sciences passed a resolution which meant that no further attempted solutions submitted to them would be examined. A few years later the Royal Society in London also banned consideration of any further 'proofs' of squaring the circle as large numbers of amateur mathematicians tried to achieve fame by presenting the Society with a solution. This decision of the Royal Society was described by De Morgan about 100 years later as the official blow to circle-squarers.
The popularity of the problem continued and there are many amusing stories told by De Morgan on this topic in his book Budget of Paradoxes which was edited and published by his wife in 1872, the year after his death. De Morgan suggests that St Vitus be made the patron saint of circle-squarers. This is a reference to St Vitus' dance, a wild leaping dance in which people screamed and shouted and which led to a kind of mass hysteria. De Morgan also suggested the term 'morbus cyclometricus' as being the 'circle squaring disease'. Clearly De Morgan found himself having to try to persuade these circle-squarers that their methods were incorrect, yet many stubbornly held to their views despite the best efforts of the professional mathematicians. For example a certain Mr James Smith wrote several books attempting to prove that . Of course Mr Smith was able to deduce from this that the circle could be squared but neither Hamilton, De Morgan nor others could convince him of his errors.
The final solution to the problem of whether the circle could be squared using ruler and compass methods came in 1880 when Lindemann proved that π was transcendental, that is it is not the root of any polynomial equation with rational coefficients. The transcendentality of π finally proves that there is no ruler and compass construction to square the circle.
One might imagine that this would be the end of interest in the problem of squaring the circle, but this was certainly not the case. It neither prevented the stream of publications claiming that π had some simple rational value, nor did it prevent the stream of publications of quite correct constructions to approximately square the circle with ruler and compass. As an example of the former type of claim, the New York Tribune published a letter in 1892 in which the author claimed to have rediscovered a secret going back to Nicomedes which proved that π = 3.2. Perhaps more surprising is the fact that there were many who were totally convinced by this letter and firmly believed thereafter that π = 3.2.
Among the correct approximate constructions to square the circle was one by Hobson in 1913. This was a fairly accurate construction which was based on constructing the approximate value of 3.14164079... for π instead of 3.14159265.... . More remarkable, however, was the ruler and compass constructions published by Ramanujan. In the Journal of the Indian Mathematical Society in 1913 in a paper named Squaring the circle Ramanujan gave a construction which was equivalent to giving the approximate value of for π, which differs from correct value only in the seventh decimal place. He ended the paper with the following:-
One of the fascinations of this problem is that it has been of interest throughout the whole of the history of mathematics. From the oldest mathematical documents known up to the mathematics of today the problem and related problems concerning π have interested both professional mathematicians and amateur mathematicians.
One of the oldest surviving mathematical writings is the Rhind papyrus, named after the Scottish Egyptologist A Henry Rhind who purchased it in Luxor in 1858. It is a scroll about 6 metres long and of a metre wide and was written around 1650 BC by the scribe Ahmes who copied a document which is 200 years older. This gives date for the original papyrus of about 1850 BC but some experts believe that the Rhind papyrus is based on a work going back to 3400 BC.
In the Rhind papyrus Ahmes gives a rule to construct a square of area nearly equal to that of a circle. The rule is to cut off the circle's diameter and to construct a square on the remainder. Although this is not really a geometrical construction as such it does show that the problem of constructing a square of area equal to that of a circle goes back to the beginnings of mathematics. This is quite a good approximation, corresponding to a value of 3.1605, rather than 3.14159, for π.
The problem of squaring the circle in the form which we think of it today originated in Greek mathematics and it is not always properly understood. The problem was, given a circle, to construct geometrically a square equal in area to the given circle. The methods one was allowed to use to do this construction were not entirely clear, for really the range of methods used in geometry by the Greeks was enlarged through attempts to solve this and other classical problems. Pappus, writing in his work Mathematical collection at the end of the period of Greek development of geometry, distinguishes three types of methods used by the ancient Greeks (see for example [5]):-
There are, we say, three types of problem in geometry, the so-called 'plane', 'solid', and 'linear' problems. Those that can be solved with straight line and circle are properly called 'plane' problems, for the lines by which such problems are solved have their origin in a plane. Those problems that are solved by the use of one or more sections of the cone are called 'solid' problems. For it is necessary in the construction to use surfaces of solid figures, that is to say, cones. There remain the third type, the so-called 'linear' problem. For the construction in these cases curves other than those already mentioned are required, curves having a more varied and forced origin and arising from more irregular surfaces and from complex motions.Now we usually think of the problem of squaring the circle to be a problem which has to be solved using a ruler and compass. This is really asking whether squaring the circle is a 'plane' problem in the terminology of Pappus given above (we shall often refer to a 'plane solution' rather than use the more cumbersome 'solutions using ruler and compass"). The ancient Greeks, however, did not restrict themselves to attempting to find a plane solution (which we now know to be impossible), but rather developed a great variety of methods using various curves invented specially for the purpose, or devised constructions based on some mechanical method.
The first mathematician who is on record as having attempted to square the circle is Anaxagoras. Plutarch, in his work On Exile which was written in the first century AD, says [4]:-
There is no place that can take away the happiness of a man, nor yet his virtue or wisdom. Anaxagoras, indeed, wrote on the squaring of the circle while in prison.Now the problem must have become quite popular shortly after this, not just among a small number of mathematicians, but quite widely, since there is a reference to it in a play Birds written by Aristopenes in about 414 BC. Two characters are speaking, Meton is the astronomer (see D Barrett (trs.), Aristophanes, Birds (London, 1978) or [4] for a shorter quote):-
Meton: I propose to survey the air for you: it will have to be marked out in acres.Now from this time the expression 'circle-squarers' came into usage and it was applied to someone who attempts the impossible. Indeed the Greeks invented a special word which meant 'to busy oneself with the quadrature'. For references to squaring the circle to enter a popular play and to enter the Greek vocabulary in this way, there must have been much activity between the work of Anaxagoras and the writing of the play. Indeed we know of the work of a number of mathematicians on this problem during this period: Oenopides, Antiphon, Bryson, Hippocrates, and Hippias.
Peisthetaerus: Good lord, who do you think you are?
Meton: Who am I? Why Meton. THE Meton. Famous throughout the Hellenic world - you must have heard of my hydraulic clock at Colonus?
Peisthetaerus (eyeing Meton's instruments): And what are these for?
Meton: Ah! These are my special rods for measuring the air. You see, the air is shaped - how shall I put it? - like a sort of extinguisher: so all I have to do is to attach this flexible rod at the upper extremity, take the compasses, insert the point here, and - you see what I mean?
Peisthetaerus: No.
Meton: Well I now apply the straight rod - so - thus squaring the circle: and there you are. In the centre you have your market place: straight streets leading into it, from here, from here, from here. Very much the same principle, really, as the rays of a star: the star itself is circular, but sends out straight rays in every direction.
Peisthetaerus: Brilliant - the man's a Thales.
Oenopides is thought by Heath to be the person who required a plane solution to geometry problems. Proclus attributes two theorems to Oenopides , namely to draw a perpendicular to a line from a given point not on the line, and to construct from a given point on a given line, a line at a given angle to the given line. Heath believes that the significance of these elementary results was that Oenopides set out for the first time the explicit 'plane' or 'ruler and compass' type of construction. Heath writes [2]:-
... [Oenopides] may have been the first to lay down the restriction of the means permissible in constructions with ruler and compasses which became a canon of Greek geometry for all plane constructions...There is no record of any attempt by Oenopides to square the circle by plane methods. In fact it is a rather remarkable fact that the Greeks did not produce fallacious 'proofs' that the circle could be squared by plane methods. The few claims for such false proofs rather seem to result from less able mathematicians failing to understand exactly what some of the more brilliant contributions to the problem were intended to show. Sadly later mathematicians did not follow the good example shown by the ancient Greeks and indeed many claimed incorrectly to have discovered a 'ruler and compass' proof. Amateur mathematicians, greatly attracted to the classical problems, have produced (and still continue to produce) thousands of false proofs.
Antiphon and Bryson both produced arguments relating to squaring the circle which were to prove important in the future development of mathematics. Antiphon inscribed a square in a circle, then a regular polygon with eight sides, then one with sixteen sides and he continued the process continually doubling the number of sides. It appears that Bryson improved the argument of Antiphon by not only inscribing polygons in a circle but also circumscribed polygons. Themistius states [1]:-
... that Bryson declared the circle to be greater than all inscribed, and less than all circumscribed polygons.Hippocrates was the first to actually use a plane construction to find a square with area equal to a figure with circular sides. He squared certain lunes, and also the sum of a lune and a circle. Now although he squared certain lunes, he had not shown that every lune can be squared. In particular the lune that he squared in his plane construction of a square of area equal to that of a certain lune and a circle was one he could not square by plane methods. Of course this lune cannot be squared by plane methods otherwise Hippocrates would have squared the circle. Although some, such as Aristotle, seemed to fail to understand the logic of Hippocrates argument, there seems little doubt that Hippocrates was perfectly aware that his methods had failed to square the circle. Examples of Hippocrates' methods of squaring lunes are given in his biography in this archive.
Hippias and Dinostratus are associated with the method of squaring the circle using a quadratrix. The curve it thought to be the invention of Hippias while its application to squaring the circle appears to be due to Dinostratus. The construction of this curve with a diagram is given in the biography of Hippias in this archive. Now this curve certainly solves the problem of squaring the circle but, as given by Hippias, the curve is constructed by mechanical means given by a uniform motion of a line in a time equal to the rotating radius of a circle. The construction was rightly criticised as requiring a knowledge of the ratio of a line and an arc of a circle, so one assumed as known the property required to square the circle in the first place. It is clear that Dinostratus never claimed that the quadratrix gave a plane method to square the circle. Nicomedes many years later also used the quadratrix to square the circle.
Aristotle did not seem to appreciate the contributions of those who had attempted to square the circle. He wrote in his work Physics :-
The exponent of any science is not called upon to solve every kind of difficulty that may be raised, but only such as arise through false deductions from the principles of the science: with others than these he need not concern himself. For example, it is for the geometer to expose the quadrature by means of segments, but it is not the business of the geometer to refute the arguments of Antiphon.In this quote "quadrature by means of segments" refers to Hippocrates quadrature of lunes which Aristotle mistakenly thinks was intended as a proof that the circle can be squared by plane methods. Antiphon's methods come in for even more criticism from Aristotle, but all credit to Antiphon whose methods contained important ideas which would lead eventually to integration. Aristotle also wrote in similar terms in Sophistical refutations again probably having had handed down to him an incorrect interpretation of what Antiphon and Bryson had attempted to show:-
The method by which Bryson tried to square the circle, were it ever so much squared thereby, is yet made sophistical by the fact that it has no relation to the matter in hand. ... The squaring of the circle by means of lunes is not eristic, but the quadrature of Bryson is eristic. The reasoning used by the former cannot be applied to any subject other than geometry alone, whereas Bryson's argument is directed to the mass of people who do not know what is possible and what is impossible in each department, for it will fit any. And the same is true of Antiphon's quadrature.Next we should consider the contributions of Archimedes to the problem of squaring the circle. Now Archimedes is famed for his introduction of the spiral curve, but why did he introduced this curve? The authors of [7] suggest three reasons:-
Is it for purely geometric reasons because he studied this curve as a means of calculating π, and squaring the circle? Is it because of his astronomical interests, trying to calculate geometrically the spiral movements of the planets? Or is it finally through the interest of a mechanical mind in a curve which results from the combination of two regular uniform movements, one in a straight line the other in a circle? these three reasons are evident at one and the same time...Archimedes gives the following definition of the spiral in his work On spirals (see [5] for example):-
If a straight line drawn in a plane revolves uniformly any number of times about a fixed extremity until it returns to its original position, and if, at the same time as the line revolves, a point moves uniformly along the straight line beginning at the fixed extremity, the point will describe a spiral in the plane.

To square the circle Archimedes gives the following construction. Let be the point on the spiral when it has completed one turn. Let the tangent at cut the line perpendicular to at . Then Archimedes proves in Proposition 19 of On spirals that is the length of the circumference of the circle with radius . Now it may not be clear that this is solved the problem of squaring the circle but Archimedes had already proved as the first proposition of Measurement of the circle that the area of a circle is equal to a right-angled triangle having the two shorter sides equal to the radius of the circle and the circumference of the circle. So the area of the circle with radius is equal to the area of the triangle .
Both Apollonius and Carpus used curves to square the circle but it is not clear exactly what these curves were. The one used by Apollonius is called by Iamblichus 'sister of the cochloid' and this has led to various guesses as to what the curve might have been. Again the curve used by Carpus of Antioch is called the 'curve of double motion' which Paul Tannery argued was the cycloid.
Now we leave the ancient Greek period and look at later developments but the first comment we should make is that the Greeks were certainly not the only ones to be interested in squaring the circle at this time. Mathematicians in India were interested in the problem (see for example [11]) while in China mathematicians such as Liu Hsiao of the Han Dynasty showed himself to be one of the prominent of those attempting to square the circle in around 25 AD.
Some time later the Arab mathematicians were, like the Greeks, fascinated by the problem. In [6] the work of al-Haytham on squaring the circle is discussed. Now al-Haytham aimed to convince people that squaring the circle was possible by a plane construction but since his promised treatise on the topic never appeared he must at least have realised that he could not solve the problem.
Not long after the work of al-Haytham, Franco of Liège in 1050 wrote a treatise De quadratura circuli Ⓣ on squaring the circle. The text is reproduced in [8] and [9] and in it Franco examines three earlier methods based on the assumption that π is or 4. Franco states (reasonably enough) that these are false, then gives his own construction which is based on the assumption that π is . Although this treatise is of great historical interest, it does show how European mathematics at the time was far behind the ancient Greeks in depth of understanding.
Moving forward to about 1450, Cusa attempted to prove that the circle could be squared by a plane construction. Although his method of averaging certain inscribed and circumscribed polygons is quite fallacious, it is one of the first serious attempts in 'modern' Europe to solve the problem. Again it is worth commenting that the ancient Greeks basically knew that the circle could not be squared by plane methods, although they stood no chance of proving it. Regiomontanus, who brought a new impetus to European mathematics, was quick to point out the error in Cusa's arguments.
The mechanical methods of the Greeks certainly appealed to Leonardo who thought about mathematics in a very mechanical way. He devised several new mechanical methods to square the circle. Many mathematicians in the sixteenth century studied the problem, including Oronce Fine and Giambattista della Porta. The 'proof' by Fine was shown to be incorrect by Pedro Nunes soon after he produced it. The beginnings of the differential and integral calculus led to an increased interest in squaring the circle, but the new era of mathematics still produced fallacious 'proofs' of plane methods to square the circle. One such false proof, given by Saint-Vincent in a book published in 1647, was based on an early type of integration. The problem was still providing much impetus for mathematical development.
James Gregory developed a deep understanding of infinite sequences and convergence. He applied these ideas to the sequences of areas of the inscribed and circumscribed polygons of a circle and tried to use the method to prove that there was no plane construction for squaring the circle. His proof essentially attempted to prove that π was transcendental, that is not the root of a rational polynomial equation. Although he was correct in what he tried to prove, his proof was certainly not correct. However, others such as Huygens, believed that π was algebraic, that is that it is the root of a rational polynomial equation.
There was still an interest in obtaining methods to square the circle which were not plane methods. For example Johann Bernoulli gave a method of squaring the circle through the formation of evolvents and this method is described in detail in [12].
The historian of mathematics, Montucla, made squaring the circle the topic of his first historical work published in 1754. This was written at a time long before the problem was finally resolved, so is necessarily very outdated. The work is, however, a classic and still well worth reading.
A major step forward in proving that the circle could not be squared using ruler and compasses occurred in 1761 when Lambert proved that π was irrational. This was not enough to prove the impossibility of squaring the circle with ruler and compass since certain algebraic numbers can be constructed with ruler and compass. It only led to a greater flood of amateur solutions to the problem of squaring the circle and in 1775 the Paris Académie des Sciences passed a resolution which meant that no further attempted solutions submitted to them would be examined. A few years later the Royal Society in London also banned consideration of any further 'proofs' of squaring the circle as large numbers of amateur mathematicians tried to achieve fame by presenting the Society with a solution. This decision of the Royal Society was described by De Morgan about 100 years later as the official blow to circle-squarers.
The popularity of the problem continued and there are many amusing stories told by De Morgan on this topic in his book Budget of Paradoxes which was edited and published by his wife in 1872, the year after his death. De Morgan suggests that St Vitus be made the patron saint of circle-squarers. This is a reference to St Vitus' dance, a wild leaping dance in which people screamed and shouted and which led to a kind of mass hysteria. De Morgan also suggested the term 'morbus cyclometricus' as being the 'circle squaring disease'. Clearly De Morgan found himself having to try to persuade these circle-squarers that their methods were incorrect, yet many stubbornly held to their views despite the best efforts of the professional mathematicians. For example a certain Mr James Smith wrote several books attempting to prove that . Of course Mr Smith was able to deduce from this that the circle could be squared but neither Hamilton, De Morgan nor others could convince him of his errors.
The final solution to the problem of whether the circle could be squared using ruler and compass methods came in 1880 when Lindemann proved that π was transcendental, that is it is not the root of any polynomial equation with rational coefficients. The transcendentality of π finally proves that there is no ruler and compass construction to square the circle.
One might imagine that this would be the end of interest in the problem of squaring the circle, but this was certainly not the case. It neither prevented the stream of publications claiming that π had some simple rational value, nor did it prevent the stream of publications of quite correct constructions to approximately square the circle with ruler and compass. As an example of the former type of claim, the New York Tribune published a letter in 1892 in which the author claimed to have rediscovered a secret going back to Nicomedes which proved that π = 3.2. Perhaps more surprising is the fact that there were many who were totally convinced by this letter and firmly believed thereafter that π = 3.2.
Among the correct approximate constructions to square the circle was one by Hobson in 1913. This was a fairly accurate construction which was based on constructing the approximate value of 3.14164079... for π instead of 3.14159265.... . More remarkable, however, was the ruler and compass constructions published by Ramanujan. In the Journal of the Indian Mathematical Society in 1913 in a paper named Squaring the circle Ramanujan gave a construction which was equivalent to giving the approximate value of for π, which differs from correct value only in the seventh decimal place. He ended the paper with the following:-
Note.- If the area of the circle be 140,000 square miles, then [the side of the square] is greater than the true length by about an inch.Among other constructions given by Ramanujan in 1914 (Approximate geometrical constructions for π, Quarterly Journal of Mathematics XLV (1914), 350-374) was a ruler and compass construction which was equivalent to taking the strange yet remarkable approximate value for π to be . Now this is 3.1415926525826461253.... which differs from π only in the ninth decimal place (π = 3.1415926535897932385...). For a circle of diameter 8000 miles, the error in the length of the side of the square constructed was only a fraction of an inch.
References (show)
- T L Heath, A history of Greek mathematics I (Oxford, 1931).
- E W Hobson, H P Hudson, A N Singh and A B Kempe, Squaring the Circle and other monographs (New York, N. Y., 1953).
- W R Knorr, The ancient tradition of geometric problems (Boston, 1986).
- I Thomas, Selections illustrating the history of Greek mathematics : Vol 1 (From Thales to Euclid) (London, 1967).
- I Thomas, Greek mathematical works (London, 1939).
- T Albertini, La quadrature du cercle d'ibn al-Haytham : solution philosophique ou mathématique?, J. Hist. Arabic Sci. 9 (1-2) (1991), 5-21, 132.
- J Delattre and R Bkouche, Why ruler and compass?, in History of Mathematics : History of Problems (Paris, 1997), 89-113.
- M Folkerts and A J E M Smeur, A treatise on the squaring of the circle by Franco of Liège, of about 1050. I, Arch. Internat. Histoire Sci. 26 (98) (1976), 59-105.
- M Folkerts and A J E M Smeur, A treatise on the squaring of the circle by Franco of Liège, of about 1050. II, Arch. Internat. Histoire Sci. 26 (99) (1976), 225-253.
- L V Gurjar, The problem of squaring the circle as solved in the Sulvasutras, J. Univ. Bombay (N.S.) 10 (5) (1942), 11-16.
- T Hayashi, A new Indian rule for the squaring of a circle: Manava'sulbasutra 3.2.9-10, Gadnita Bharati 12 (3-4) (1990), 75-82.
- J E Hofmann, Johann Bernoullis Kreisrektifikation durch Evolventenbildung, Centaurus 29 (2) (1986), 89-99.
- S Wagon, Circle-squaring in the twentieth century (Czech), Pokroky Mat. Fyz. Astronom. 28 (6) (1983), 320-328.
- A Wasserstein, Some early Greek attempts to square the circle, Phronesis 4 (1959), 92-100.
- J Zackova, The problem of squaring the circle and Lambert's proof of the irrationality of the number π (Czech), Pokroky Mat. Fyz. Astronom. 11 (1966), 240-250.
Additional Resources (show)
Other pages about Squaring the circle:
Written by J J O'Connor and E F Robertson
Last Update April 1999
Last Update April 1999