Leonard Adleman
Quick Info
San Francisco, California, USA
Biography
Leonard Adleman's father was an appliance salesman, his mother a bank teller. As a young boy growing up in San Francisco, Adleman had little ambition, far less of becoming a mathematician. By his own admission, he was [1] "incredibly naive and immature". However, it was his high school English teacher who made him realize the beauty of ideas through a reading of Hamlet. It was at the suggestion of this teacher who had opened his eyes "to the fact that one could see things more deeply than the purely superficial" that Adleman enrolled at the University of California at Berkeley. Still hesitant and undecided, he first declared to be a chemist (inspired by years of watching Mr.Wizard on television), then a doctor (inspired by his Kappa Nu fraternity brothers) before settling on a mathematics major. [1]I had gone through a zillion things and finally the only thing that was left where I could get out in a reasonable time was mathematics.It took him five years to finally graduate in 1968 when he took a job as a computer programmer at the Bank of America. Soon after, he applied to medical school where he was accepted but he changed his mind and did not enroll. He decided instead to be a physicist and began taking classes at the San Francisco State College while working at the bank. Once again he lost interest.
I didn't like doing experiments, I liked thinking about things.Adleman eventually returned to Berkeley for pursuing a PhD in computer science. He had two motivations, the first being practical:-
I thought that getting a PhD in computer science would at least further my career.The second was more romantic. Martin Gardner had written an article on Gödel's theorem in Scientific American which overwhelmed Adleman with its deep philosophical implications:-
I thought 'Wow. This is so neat.' There were several things I found neat - black holes, general relativity. I thought for once in my life, I want to really understand one of these deep results.Adleman decided to join graduate school and come away with an understanding of Gödel's theorem at a level beyond the superficial. However, while in graduate school, something else happened to him -- he finally understood the true nature and compelling beauty of mathematics. He discovered that it was "... less related to accounting than it is to philosophy."
People think of mathematics as some kind of practical art, ... the point when you become a mathematician is where you somehow see through this and see the beauty and power of mathematics.In 1976, Adleman completed his thesis "Number Theoretic Aspects of Computational Complexities", received his PhD, and immediately secured a job as an assistant professor of mathematics at MIT. (His father advised him to stay with the Bank of America where atleast they had a good retirement plan). One of Adleman's colleagues at MIT was Ronald Rivest who had his office next door. Rivest had been gripped by an article in The IEEE Transactions on Information Theory written by Martin Hellman, a computer scientist at Stanford, and his student Whitfield Diffie (see [2]). In it, they had described an idea for a new kind of encryption system. It was based on introducing new secret "keys" -- mathematical formulas for scrambling and unscrambling messages. Up until then, anyone in possession of an encrypting key could also decrypt by simply reversing the encryption instructions. What Hellman and Diffie proposed was quite revolutionary -- use one-way functions or mathematical formulas that are easy to compute in one direction but impossible to do in the reverse unless one knew how they were constructed in the first place. The encryption key could be made public so that anyone could send an encoded message. But only someone having the actual construction of the key would have the decryption key and thus be able to decode it.
Rivest announced that such a one-way function would be found which would lead to the creation of a public key cryptosystem. The idea itself was manifestly workable but finding a truly one-way function seemed a formidable task. Rivest had an equally enthusiastic supporter in one of his colleagues -- Adi Shamir. Adleman however was less than excited -- he thought the idea was quite impractical and unworthy of pursuing. Soon however, Rivest and Shamir were inventing coding systems and Adleman agreed to test each of the systems by trying to break it. The duo came up with 42 different coding systems and each time Adleman was able to break it. On the 43rd attempt, based on a difficult factoring problem, Adleman confessed that the code was really unbreakable because of the mathematics involved and could presumably take centuries of computation to factor. Rivest stayed up all night, preparing the manuscript describing the code before he handed it to Adleman. He had listed the paper's authors in alphabetical order - Adleman, Rivest, Shamir. Adleman demurred:-
I told Ron, 'Take my name off the paper. It's your work'.But Rivest insisted and eventually prevailed upon him.
I thought, 'Well, it's going to be the least important paper I've ever been on, but in a few years I will need so many lines on my vita to get tenure, ... on the other hand, I did do a substantial amount of intellectual work breaking the codes 1 through 42. So the reasonable thing to do is be the third author'.Martin Gardner wrote about the code, now called RSA after the persons involved, in his column (see [3]) and much to Adleman's astonishment, their fame and that of the code spread rapidly. A barrage of letters poured in and the National Security Agency (NSA), hitherto the only place where encryption was studied, expressed fears that the publication of seemingly unbreakable codes like RSA might potentially jeopardise national security!
Rivest, Shamir and Adleman assigned the patent for their code to MIT and in 1983 formed a company, RSA Data Security Inc. of Redwood City, California, to make RSA computer chips. Adleman was made president, Rivest chairman of the board and Shamir the treasurer. In 1996, the company was sold for $200 million.
MIT provided Adleman with an intellectually stimulating atmosphere but he yearned for California where he wanted to settle down and have a family. Accordingly, he took up a job at the University of Southern California in Los Angeles (where he is presently the Henri Salvatori Professor of Computer Science and Professor of Molecular Biology) in 1980. Three years later, he met his future wife Lori Bruce at a singles dance. It was love at first sight and the couple got married six weeks later.
In that same year, Adleman, along with R S Rumely and C Pomerance, published a paper describing a 'nearly polynomial time' deterministic algorithm for the problem of distinguishing prime numbers from composite ones. It was the first ever result in theoretical computer science to be published in Annals of Mathematics (see [4]).
The year also witnessed a landmark development in computer science. Fred Cohen, a graduate student at USC, put forth a new idea regarding "a program that can 'infect' other programs by modifying them to include a possibly modified version of itself". Adleman, who was Cohen's supervisor, was immediately convinced that the idea would work the moment he learned about it. He proposed the name 'virus' for the program to Cohen who eventually published his first virus paper in 1984 and his PhD dissertation on the same topic in 1986.
A key turning point in Adleman's life came during the early 90's when he directed his enthusiasm towards the field of immunology. One of the reasons for his growing interest in it was that unsolved problems in immunology "had the kind of beauty mathematicians look for"[5]. Adleman was soon preoccupied with the study of white blood cells called T lymphocytes whose steady decline in AIDS patients leave them vulnerable to lethal infections. The T cells are primarily of two types - CD4 and CD8. There are about 800 CD4 T cells in each cubic millimeter of blood plasma in healthy and newly infected persons. This number however, declines gradually during the decade-long latency period associated with AIDS. Typically, after CD4 cell count drops below 200, infections characteristic of AIDS set in. However, "losing a T cell is not like losing an arm or a leg"[5]. The human body, even that of an HIV-infected person, can replenish the T cell count by making new ones. It was quite mysterious why CD4 T cell population shrank in HIV-infected patients.
Adleman and others suggested that the problem lay in the homeostatic mechanism which monitors the levels of T cells - it does not distinguish between CD4 and CD8 cells. Thus every time it detects the loss of T cells, the homeostatic mechanism generates both CD4 and CD8 cells to restore the total T cell-count. However, addition of CD8 cells effectively suppresses the production of CD4 cells and consequently HIV continues attacking CD4, thus lowering its count. As Adleman put it [5]:-
The homeostatic mechanism ... is blind.Adleman and David Wofsy of the University of California at San Francisco described their test of the hypothesis in the February 1993 issue of Journal of Acquired Immune Deficiency Syndromes (JAIDS)(see [6]). Unfortunately, the AIDS research community's responses to Adleman's ideas were less than encouraging. Undeterred, Adleman decided to acquire a deeper understanding of the biology of HIV in order to be a more persuasive advocate. He entered the molecular biology lab at USC and began to learn the methods of modern biology under the guidance of Nickolas Chelyapov (now chief scientist in Adleman's own laboratory).
It was a period of intense learning for Adleman whose own earlier views on biology was undergoing a significant transformation. He explains why [7]:-
Biology was now the study of information stored in DNA -- strings of four letters: A, T, G and C for the bases adenine, thymine, guanine and cytosine -- and of the transformations that information undergoes in the cell. There was mathematics here!He began reading the classic text The Molecular Biology of the Gene, co-authored by James D. Watson (see [13]) of Watson-Crick fame. Adleman vividly recounts the time he studied the description of a rather special enzyme [7]:-
Late one evening, while lying in bed reading Watson's text, I came to a description of DNA polymerase. This is the king of enzymes - the maker of life. Under appropriate conditions, given a strand of DNA, DNA polymerase produces a second "Watson-Crick" complementary strand, in which every C is replaced by a G, every G by a C, every A by a T and every T by an A. For example, given a molecule with the sequence CATGTC, DNA polymerase will produce a new molecule with the sequence GTACAG. The polymerase enables DNA to reproduce, which in turn allows cells to reproduce and ultimately allows you to reproduce. For a strict reductionist, the replication of DNA by DNA polymerase is what life is all about.He continues:-
DNA polymerase is an amazing little nanomachine, a single molecule that "hops" onto a strand of DNA and slides along it, "reading" each base it passes and "writing" its complement onto a new, growing DNA strand.It was Adleman's moment of epiphany:-
While lying there admiring this amazing enzyme, I was struck by its similarity to something described in 1936 by Alan Turing, the famous British mathematician.Indeed, Adleman was thinking about the "Turing machine".
One version of his machine consisted of a pair of tapes and a mechanism called a finite control, which moved along the "input" tape reading data while simultaneously moving along the "output" tape reading and writing other data. The finite control was programmable with very simple instructions, and one could easily write a program that would read a string of A, T, C and G on the input tape and write the Watson-Crick complementary string on the output tape. The similarities with DNA polymerase could hardly have been more obvious.Even more was true:-
But there was one important piece of information that made this similarity truly striking: Turing's toy computer had turned out to be universal - simple as it was, it could be programmed to compute anything that was computable at all. (This notion is essentially the content of the well-known "Church's thesis".) In other words, one could program a Turing machine to produce Watson-Crick complementary strings, factor numbers, play chess and so on.Adleman could hardly contain his excitement:-
This realization caused me to sit up in bed and remark to my wife, Lori, "Jeez, these things could compute." I did not sleep the rest of the night, trying to figure out a way to get DNA to solve problems.He readily decided to make a DNA computer similar to a Turing machine with an enzyme replacing the finite control. A decade earlier, IBM researchers Charles H. Bennet and Rolf Landauer had suggested essentially similar ideas (see [8]) but there was uncertainty regarding the existence of enzymes which not only produced Watson-Crick complements but were able to perform other mathematical functions as well. Adleman wanted his DNA computer to perform something at least as interesting as playing chess. To this end, he began learning the essential tools of DNA chemistry like polymerases, ligases, gel electrophoresis, DNA synthesis etc. The fact that commercial DNA, tailor-made to specific requirements, was readily available was more than helpful for his purpose.
It is now possible to write a DNA sequence on a piece of paper, send it to a commercial synthesis facility and in a few days receive a test tube containing approximately molecules of DNA, all (or atleast most) of which have the described sequence. ... The molecules are delivered dry in a small tube and appear as a small, white, amorphous lump.Theoretically, only two things were needed to build a computer capable of computing anything computable - a method by which information was stored and simple operations which acted on it. DNA itself was a storehouse for information (it contains the 'blueprint of life'!) while enzymes like polymerases had been used to operate on this information. Adleman knew he had enough to build a universal computer.
The very next thing he had to do was to select a problem which his DNA computer would be able to solve. Adleman decided upon the Hamiltonian Path Problem.
... given a graph with directed edges and a specified start vertex and end vertex, one says there is a Hamiltonian path if and only if there is a path that starts at the start vertex, ends at the end vertex and passes through each remaining vertex exactly once. The Hamiltonian Path Problem is to decide for any given graph with specified start and end vertices whether a Hamiltonian path exists or not.Although the Hamiltonian Path Problem has been studied extensively, an efficient algorithm to solve it is yet to emerge. It was shown during the early 1970's that no efficient algorithm for the problem is at all possible (proving it is still an open problem!). In fact, it belongs to a larger class of problems known as "NP-complete" problems. However, there are algorithms such as the following which work nevertheless:
Given a directed graph with vertices, having start vertex and end vertex ,
- Generate a set of random paths throughout the graph.
- Remove any path that does not begin with and end with .
- Remove any path that does not enter exactly vertices.
- Remove any path that does not passes through each vertex at least once.
- If the set is non-empty, say "Yes"; otherwise, say "No".
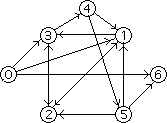
Though not an efficient one, this algorithm gives reasonably correct results provided paths are generated randomly enough and the resulting sets are large enough. It was precisely this algorithm which Adleman used in his first DNA computation. For his Hamiltonian Path Problem, he chose the following directed graph:
In this graph, the start and end vertices for the Hamiltonian path are respectively 0 and 6. Adleman first assigned a random DNA sequence to each vertex and edge in the graph (the sequences are known as oligonucleotides). Because each DNA sequence has its Watson-Crick complement, each vertex is associated with its complement sequence. Once the encodings were set in place, the complementary DNA sequences for the vertices and the sequences for the edges were synthesized. The remaining procedures are best described by Adleman himself:-
I took a pinch (about molecules) of each of the different sequences and put them into a common test tube. To begin the computation, I simply added water - plus ligase, salt and a few other ingredients to approximate the conditions inside a cell. Altogether only about one fiftieth of a teaspoon of solution was used. Within about one second, I had the answer to the Hamiltonian Path Problem in my hand.Adleman had to then perform a rather tedious experiment by which he had to weed out about a 100 trillion molecules that encoded non-Hamiltonian paths. The fact that he implemented the algorithm described above meant that any DNA remaining in the test tube after every preceding steps were carried out should necessarily encode the desired Hamiltonian path. In the end, it took Adleman seven days in the molecular biology lab to perform the world's first DNA computation.
Adleman reported his brilliant discovery in the November 1994 issue of Science (see [9]) and he is now rightly hailed as the 'father of DNA computation'. One of the most exciting fields in contemporary scientific research, molecular computation has witnessed some remarkable breakthroughs in the years following Adleman's experiment. In 1995, Richard J. Lipton at Princeton University proposed (see [10]) a DNA solution to another famous 'NP-complete' problem - the so-called "satisfaction" problem (SAT). In 2002, a research team led by Ehud Shapiro at the Weizmann Institute of Science in Rehovet, Israel devised a molecular computing machine composed of enzymes and DNA molecules which could perform 330 trillion operations per second, more than 100,000 times the speed of the fastest PC. Within months, the same team improved on their previous model with one in which the DNA input is also the source of fuel for the machine (see [12]). The Guinness Book of Records recognized the computer as 'the smallest biological computing device'[11] ever constructed.
Such DNA computing devices have revolutionary implications in the pharmaceutical and biomedical fields. Scientists foresee a future where tiny DNA computers would be able to monitor our well-being and release the right drug to repair damaged tissues. Says Shapiro [11]:-
Autonomous bio-molecular computers may be able to work as 'doctors in a cell', operating inside living cells and sensing anomalies in the host ... Consulting their programmed medical knowledge, the computers could respond to anomalies by synthesizing and releasing drugs.David Hawksett, the science judge at the Guinness World Records, puts it aptly [11]:-
This is an area of research that leaves the science fiction writers struggling to keep up.This 'doctor-in-a-cell' vision for molecular computation is only one of many others being vigorously pursued by scientists who are now the torchbearers of the new 'molecular science' which attempts to penetrate deep into the hidden mysteries of life. It is indeed remarkable that the marriage of the seemingly disparate yet equally fecund fields of biology and mathematics has fostered such an enterprise. No less inspirational, in this age of fierce specialization, is the fact that it was a mathematician who started it all. Perhaps someday we might vindicate Adleman's vision [7]:-
In the past half-century, biology and computer science have blossomed, and there can be little doubt that they will be central to our scientific and economic progress in the new millenium. But biology and computer science - life and computation - are related. I am confident that at their interface great discoveries await those who seek them.
References (show)
- G Kolata, 'Hitting the High Spots of Computer Theory: Leonard Adleman', The New York Times, December 13, 1994.
- W Diffie and M Hellman, 'New Directions in Cryptography', IEEE Transactions on Information Theory, vol. IT-22, November 1976, pp. 644-654.
- M Gardner, 'Mathematical Games: A new kind of cipher that would take millions of years to break', Scientific American, August 1977, pp. 120-124.
- L Adleman, R S Rumely, C Pomerance, 'On Distinguishing Prime Numbers from Composite Numbers', Annals of Mathematics, 117, 1983, pp. 173-206.
- J Rennie, 'Balanced Immunity', Scientific American, May 1993, pp. 10-11.
- L Adleman and David Wofsy, 'T-cell Homeostasis: Implications in HIV', JAIDS, 1993, pp. 144-152.
- L Adleman, 'Computing with DNA', Scientific American, August 1998, pp. 34-41.
- C H Bennet and R Landauer, 'The Fundamental Physical Limits of Computation', Scientific American, July 1985, pp. 38-46.
- L Adleman, 'Molecular Computation of Solutions to Combinatorial Problems', Science, 266, November 11, 1994, pp. 1021-1024.
- R J Lipton, 'DNA Solution of Hard Computational Problems', Science, 268, April 28 1994, pp. 542-545.
- S Lovgren, 'Computer Made from DNA and Enzymes', National Geographic News , February 24, 2003. http://news.nationalgeographic.com/news/2003/02
- E Shapiro, B Gill, R Adar, U Ben-Dor and Y Benenson, 'An Autonomous Molecular Computer for Logical Control of Gene Expression', Nature, 429, pp. 423-429 (Published online on April 28, 2004).
- J D Watson, N H Hopkins, J W Roberts, J A Steitz, A M Weiner, 'Molecular Biology of the Gene' (Benjamin/Cummings, Menlo Park, CA, ed. 3, 1987).
Additional Resources (show)
Other websites about Leonard Adleman:
Honours (show)
Honours awarded to Leonard Adleman
Written by Saikat Biswas, University of St Andrews
Last Update May 2005
Last Update May 2005
