Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji

Quick Info

Born

13 April 0953
Baghdad (now in Iraq)

Died

about 1029

---

Summary

Al-Karaji was an Islamic mathematician who wrote about the work of earlier mathematicians and who can be regarded as the first person to free algebra from geometrical operations and replace them with the type of operations which are at the core of algebra today.

Biography

The first comment that we must make regards al-Karaji's name. It appears both as al-Karaji and as al-Karkhi but this is not a simple matter of two different transliterations of the same Arabic name. The significance is that Karaj is a city in Iran and if the mathematician's name is al-Karaji then certainly his family were from that city. On the other hand Karkh is one of the original suburbs of Baghdad which grew up outside the southern gate of the original city. The name al-Karkhi would indicate that the mathematician came from the suburb of Baghdad.

Historians seem divided as to which of these interpretations is correct. The version al-Karkhi was proposed by Woepcke (see [7] or [8]) but al-Karaji, the version which is most often used in texts today, was suggested as most likely by della Vida in 1933. Rashed comments (see [1] or [5]):-

In the present state of our knowledge delle Vida's argument is plausible but not decisive. On the basis of the manuscripts consulted it is far from easy to decide in favour of either name.

Certainly we know that al-Karaji lived in Baghdad for most of his life and that his chief mathematical works were written during the time when he lived in that city. His important treatise on algebra Al-Fakhri was dedicated to the ruler of Baghdad and was written in the city. However, at some later point in his career, al-Karaji left Baghdad to live in what are described as the "mountain countries". He seems to have given up mathematics at this time and concentrated on engineering topics such as the drilling of wells.

The importance of al-Karaji in the development of mathematics is viewed rather differently by different authors. The reason for this, rather in the same spirit as the different views on al-Khwarizmi, depends on the significance one attaches to the style of his mathematics. Some consider that his work is merely reworking ideas from earlier mathematicians while others see him as the first person to completely free algebra from geometrical operations and replace them with the arithmetical type of operations which are at the core of algebra today.

Crossley [3] sounds relatively unimpressed by al-Karaji's contributions (although he describes the content accurately):-

[Al-Karaji] gives rules for the arithmetic operations including (essentially) the multiplication of polynomials. ... al-Karaji usually gives a numerical example for his rules but does not give any sort of proof beyond giving geometrical pictures. Often he explicitely says that he is giving a solution in the style of Diophantus. He does not treat equations above the second degree except for ones which can easily be reduced to at most second degree equations followed by the extraction of roots. The solutions of quadratics are based explicitly on the Euclidean theorems ...

Woepcke in [7] (see also the reprint [8]) was the first historian to realise the importance of al-Karaji's work and later historians mostly agree with his interpretation. He describes it as the first appearance of a:-

... theory of algebraic calculus ... .

Rashed (see [5] which contains Rashed's article from [1] and other writings by Rashed on al-Karaji) agrees with Woepcke's interpretation and perhaps goes even further in stressing al-Karaji's importance. He writes:-

... the more-or-less explicit aim of [al-Karaji's] exposition was to find the means of realising the autonomy and specificity of algebra, so as to be in a position to reject, in particular, the geometric representation of algebraic operations.

To give another quote from Rashed's description of al-Karaji's contribution:-

Al-Karaji's work holds an especially important place in the history of mathematics. ... the discovery and reading of the arithmetical work of Diophantus, in the light of the algebraic conceptions and methods of al-Khwarizmi and other Arab algebraists, made possible a new departure in algebra by Al-Karaji ...

So what was this new departure in algebra? Perhaps it is best described by al-Samawal, one of al-Karaji's successors, who described it as [5]:-

... operating on unknowns using all the arithmetical tools, in the same way as the arithmetician operates on the known.

What al-Karaji achieved in Al-Fakhri was first to define the monomials $x, x^{2}, x^{3}, ...$ and $\Large \frac 1 {x}\normalsize, \Large \frac 1 {x^2}\normalsize, \Large \frac 1 {x^3}\normalsize, ...$ and to give rules for products of any two of these. So what he achieved here was defining the product of these terms without any reference to geometry. In fact he almost gave the formula

$x^{n}x^{m} = x^{m+n}$ for all integers $n$ and $m$

but he failed to make the definition $x^{0} = 1$ so he fell just a little short.

Having given rules for multiplication and division of monomials al-Karaji then looked at "composite quantities" or sums of monomials. For these he gave rules for addition, subtraction and multiplication but not for division in the general case, only giving rules for the division of a composite quantity by a monomial. He was able to give a rule for finding the square root of a composite quantity which is not completely general since it required the coefficients to be positive, but it is still a remarkable achievement.

Al-Karaji also uses a form of mathematical induction in his arguments, although he certainly does not give a rigorous exposition of the principle. Basically what al-Karaji does is to demonstrate an argument for $n = 1$, then prove the case $n = 2$ based on his result for $n = 1$, then prove the case $n = 3$ based on his result for $n = 2$, and carry on to around $n = 5$ before remarking that one can continue the process indefinitely. Although this is not induction proper, it is a major step towards understanding inductive proofs.

One of the results on which al-Karaji uses this form of induction comes from his work on the binomial theorem, the binomial coefficients and the Pascal triangle. In Al-Fakhri al-Karaji computed $(a+b)^{3}$ and in Al-Badi he computed $(a-b)^{3}$ and $(a+b)^{4}$. The general construction of the Pascal triangle was given by al-Karaji in work described in the later writings of al-Samawal. In the translation by Rashed and Ahmad (see for example [5]) al-Samawal writes:-

Let us now recall a principle for knowing the necessary number of multiplications of these degrees by each other, for any number divided into two parts. Al-Karaji said that in order to succeed we must place 'one' on a table and 'one' below the first 'one', move the first 'one' into a second column, add the first 'one' to the 'one' below it. Thus we obtain 'two', which we put below the transferred 'one' and we place the second 'one' below the 'two'. We have therefore 'one', 'two', and 'one'.

To see how the second column of 1,2,1 corresponds to squaring a+b al-Samawal continues to describe Al-Karaji's work writing:-

This shows that for every number composed of two numbers, if we multiple each of them by itself once - since the two extremes are 'one' and 'one' - and if we multiply each one by the other twice - since the intermediate term is 'two' - we obtain the square of this number.

This is a beautiful description of the binomial theorem using the Pascal triangle. The description continues up to the binomial coefficients which give $(a+b)^{5}$ but we shall only quote how al-Karaji constructs the third column from the second:-

If we transfer the 'one' in the second column into a third column, then add 'one' from the second column to 'two' below it, we obtain 'three' to be written under the 'one' in the third column. If we then add 'two' from the second column to ''one' below it we have 'three' which is written under the 'three', then we write 'one' under this 'three'; we thus obtain a third column whose numbers are 'one', 'three', 'three', and 'one'.

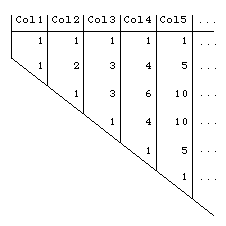
The table al-Karaji constructed looks like the Pascal triangle on its side.

Other results obtained by al-Karaji include summing the first $n$ natural numbers, the squares of the first $n$ natural numbers and the cubes of these numbers. He proved that the sum of the first $n$ natural numbers was ${1\over2}n(n + 1)$. He also gave (in Rashed and Ahmad's translation, see for example [5]):-

The sum of the squares of the numbers that follow one another in natural order from one is equal to the sum of these numbers and the product of each of them by its predecessor.

In modern notation this result is

$\sum i ^{2} = \sum i + \sum i (i - 1)$.

Al-Karaji also considered sums of the cubes of the first $n$ natural numbers writing (in Rashed and Ahmad's translation, see for example [5]):-

If we want to add the cubes of the numbers that follow one another in their natural order we multiply their sum by itself.

In modern notation

$\sum i ^{3} = (\sum i)^{2}$.

Al-Karaji showed that $(1 + 2 + 3 + ... + 10)^{2}$ was equal to $1^{3} + 2^{3} + 3^{3} + ... + 10^{3}$. He did this by first showing that $(1 + 2 + 3 + ... + 10)^{2} = (1 + 2 + 3 + ... + 9)^{2} + 10^{3}$. He could now use the same rule on $(1 + 2 + 3 + ... + 9)^{2}$, then on $(1 + 2 + 3 + ... + 8)^{2}$ etc. to get

$( 1 + 2 + ... + 10)^{2}$
$= (1 + 2 + 3 + ... + 8)^{2} + 9^{3} + 10^{3}$
$= (1 + 2 + 3 + ... + 7)^{2} + 8^{3} + 9^{3} + 10^{3}$
= . . .
$= 1^{3} + 2^{3} + 3^{3} + ... + 10^{3}.$

Finally we should mention the influence of Diophantus on al-Karaji. The first five books of Diophantus's Arithmetica had been translated into Arabic by ibn Liqa around 870 and these were studied by al-Karaji. Woepcke in his introduction to Al-Fakhri ([7] or [8]) writes that he found:-

... more than a third of the problems of the first book of Diophantus, the problems of the second book starting with the eighth, and virtually all the problems of the third book were included by al-Karaji in his collection.

Al-Karaji also invented many new problem of his own but even those of Diophantus were certainly not just taken without further development. He always tried to generalise Diophantus's results and to find methods which were more generally applicable.

It was not only to algebra that al-Karaji contributed. The paper [9] discusses some of his geometrical work. This occurs in a chapter entitled On measurement and balances for measuring of buildings and structures. al-Karaji defines points, lines, surfaces, solids and angles. He also gives rules for measuring both plane and solid figures, often using arches as examples. He also gives methods of weighing different substances.

References (show)

1. R Rashed, Biography in Dictionary of Scientific Biography (New York 1970-1990).
   See THIS LINK.
2. A A al'Daffa, The Muslim contribution to mathematics (London, 1978).
3. J N Crossley, The emergence of number (Singapore, 1980).
4. O Neugebauer, The exact sciences in antiquity (New York, 1969).
5. R Rashed, The development of Arabic mathematics : between arithmetic and algebra (London, 1994).
6. R Rashed, Entre arithmétique et algèbre: Recherches sur l'histoire des mathématiques arabes (Paris, 1984).
7. F Woepcke, Extrait du Fakhri, traité d'Algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi (Paris, 1853).
8. F Woepcke, Extrait du Fakhrî, traité d'algèbre par Abou Bekr Mohammed Ben Alhacan Alkarkhi, Reprint of the 1853 original (Hildesheim, 1982).
9. M A Abrarova, The geometrical section of al-Karaji's treatise 'Comprehensive book of arithmetic' (Russian), in Mathematics and astronomy in the works of Ibn Sina, his contemporaries and successors (Tashkent, 1981), 118-125.
10. M A Abrarova, The algebraic section of al-Karaji's treatise, the 'Comprehensive book of arithmetic', in On the history of medieval Eastern mathematics and astronomy (Tashkent, 1983), 49-53.
11. M A Abrarova, al-Karaji and his Universal book of arithmetic (Russian), in Mathematics and astronomy in the works of scientists of the medieval East (Tashkent, 1977), 107-113, 139.
12. M A Abrarova, Development of al-Khwarizmi's ideas in the works of al-Karaji (Russian), in The great medieval scientist al-Khwarizmi (Tashkent, 1985), 247-251.
13. H A Al-Tayyar, Investigation of Al-Karji's conditions for a perfect square, in Frege conference Schwerin, 1984 (Berlin, 1984), 42-43.
14. A R Amir-Moéz, Comparison of the methods of Ibn Ezra and Karkhi, Scripta Math. 23 (1957), 173-178.
15. L S Mokhamed, On negative numbers in al-Karaji's works (Russian), in History and methodology of the natural sciences No. XXV (Moscow, 1980), 115-120.
16. L S Mohammed, The Sufficient book of al-Karaji (Russian), in History and methodology of the natural sciences No. XX (Moscow, 1978), 111-121.
17. K H Parshall, The art of algebra from al-Khwarizmi to Viète : a study in the natural selection of ideas, Hist. of Sci. 26 (72, 2) (1988), 129-164.
18. R Rashed, L'induction mathématique-al-Karaji et As-Samaw'al, Arch. Hist. Exact Sci. 1 (1972), 1-21.
19. B A Rozenfel'd, A system of linear equations in Diophantus and al-Karaji (Russian), Istor.-Mat. Issled. No. 27 (1983), 142-146.
20. J Sesiano, Le traitement des équations indéterminées dans le Badi fi al-Hisab d'Abu Bakr Al-Karaji, Arch. History Exact Sci. 17 (4) (1977), 297-379.
21. S Shalhub, The calculations and algebra of abu Kamil Shuja- ibn Aslam and his effects on the work of al-Karaji and on the work of Leonardo Fibonacci (Arabic), in Deuxième Colloque Maghrebin sur l'Histoire des Mathématiques Arabes (Tunis, 1990), A23-A39.

Additional Resources (show)

Other pages about al-Karaji:

1. See al-Karaji on a timeline
2. Heinz Klaus Strick biography

Other websites about al-Karaji:

1. Dictionary of Scientific Biography
2. MathSciNet Author profile

Honours (show)

Honours awarded to al-Karaji

1. Popular biographies list Number 168

Cross-references (show)

1. History Topics: Arabic mathematics : forgotten brilliance?
2. History Topics: Infinity
3. Other: Earliest Uses of Symbols for Fractions
4. Other: Most popular biographies – 2024

Written by J J O'Connor and E F Robertson
Last Update July 1999