Hippias of Elis
Quick Info
Elis, Peloponnese, Greece
Biography
Hippias of Elis was a statesman and philosopher who travelled from place to place taking money for his services. He lectured on poetry, grammar, history, politics, archaeology, mathematics and astronomy. Plato describes him as a vain man being both arrogant and boastful, having a wide but superficial knowledge. Heath tells us something of this character when he writes in [3]:-He claimed ... to have gone once to the Olympian festival with everything that he wore made by himself, ring and sandal (engraved), oil-bottle, scraper, shoes, clothes, and a Persian girdle of expensive type; he also took poems, epics, tragedies, dithyrambs, and all sorts of prose works.As to Hippias's academic achievements, Heath writes:-
He was a master of the science of calculation, geometry, astronomy, 'rhythms and harmonies and correct writing'. He also had a wonderful system of mnemonics enabling him, if he once heard a string of fifty names to remember them all.A rather nice story, which says more of the Spartans than it does of Hippias, is that it was reported that he received no payment for the lectures he gave in Sparta since [3]:-
... the Spartans could not endure lectures on astronomy or geometry or calculation; it was only a small minority of them who could even count; what they liked was history and archaeology.Since Hippias was reported to give lectures on archaeology, he seems to have chosen the wrong topics when he lectured in Sparta!
Hippias's only contribution to mathematics seems to be the quadratrix which may have been used by him for trisecting an angle and squaring the circle. The curve may be used for dividing an angle into any number of equal parts. Perhaps the highest compliment that we can pay to Hippias is to report on the arguments of certain historians of mathematics who have claimed that the Hippias who discovered the quadratrix cannot be Hippias of Elis since geometry was not far enough advanced at this time to have allowed him to make these discoveries. However, their arguments are not generally accepted and there is ample evidence to attribute the discovery of the quadratrix to Hippias of Elis.
Heath [3] writes:-
It was probably about 420 BC that Hippias of Elis invented the curve known as the quadratrix for the purpose of trisecting any angle.However this is far from certain and there is some evidence to suggest that Geminus, writing in the first century BC, had in his possession a treatise by Hippias of Elis on the quadratrix which indicated how it could be used to square the circle. If this is indeed the case then the treatise by Hippias must have been lost between this time and that of Sporus in the third century AD.
Pappus wrote his major work on geometry Synagoge in 340. It is a collection of mathematical writings in eight books. Book IV contains a description of the quadratrix of Hippias.
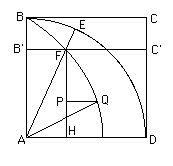
Look at the diagram of the quadratrix.
is a square and is part of a circle, centre radius . As the radius rotates about to move to the position then the line moves at the same rate parallel to itself to end at . Then the locus of the point of intersection of the rotating radius and the moving line is the quadratrix. Hence
,
so, taking ,
angle = arc = .
To divide the angle in a given ratio, say , then draw a point on the line dividing it in the ratio .
Draw a line through parallel to to meet the quadratrix at . Then divides angle in the ratio .
Pappus also gives the rather more complicated version of the construction necessary to square the circle. However, Pappus reports that Sporus had two criticisms of Hippias's method with which he agrees. The second is specifically related to the construction necessary for squaring the circle which we have not described. The first however relates to the construction of the quadratrix itself. Pappus reports that Sporus writes (see [3]):-
The very thing for which the construction is thought to serve is actually assumed in the hypothesis. For how is it possible, with two points starting from B, to make one of them move along a straight line to A and the other along a circumference to D in an equal time, unless you first know the ratio of the straight line AB to the circumference BED? In fact this ratio must also be that of the speeds of motion. For, if you employ speeds not definitely adjusted to this ratio, how can you make the motions end at the same moment, unless this should sometime happen by pure chance? Is not the thing thus shown to be absurd?The point here seems to be a question of what exactly Hippias is trying to show with his quadratrix. Certainly he knew perfectly well that he was not providing a ruler and compass construction for squaring the circle. Exactly what he has proved concerning squaring the circle is, as Pappus and Sporus suggest, far from clear.
References (show)
- I Bulmer-Thomas, Biography in Dictionary of Scientific Biography (New York 1970-1990).
See THIS LINK. - Biography in Encyclopaedia Britannica.
http://www.britannica.com/biography/Hippias - T L Heath, A History of Greek Mathematics I (Oxford, 1921).
- M Cantor, Vorlesungen über Geschichte der Mathematik I (Leipzig, 1908), 193-197.
Additional Resources (show)
Other pages about Hippias:
Other websites about Hippias:
Cross-references (show)
Written by J J O'Connor and E F Robertson
Last Update January 1999
Last Update January 1999