Taylor Series

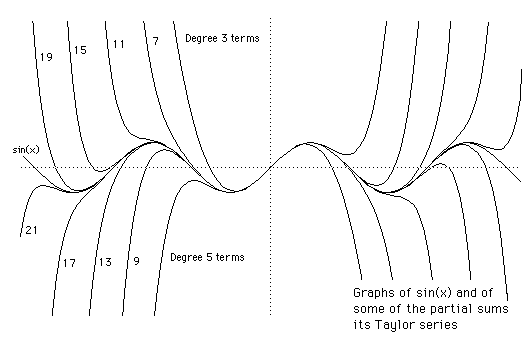
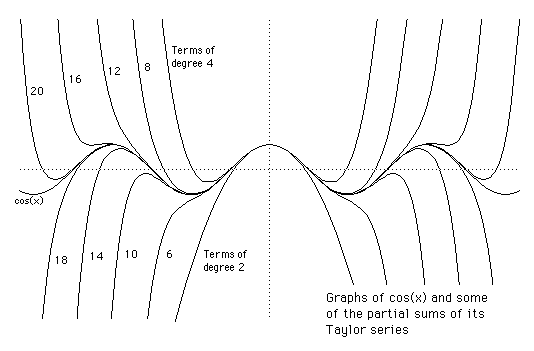
Many functions can be written as powers series about some point of their domain. About a point

a

(say) we get

f(a + h) = f(a) + \large\frac{1}{1!}\normalsize f'(a)h + \large\frac{1}{2!}\normalsize f''(a)h^{2} + \large\frac{1}{3!}\normalsize f'''(a)h^{3} + ...

which we call the Taylor series of

f

.

The case

a=0

is known as the Maclaurin series of

f

.

The Taylor Series for

\sin(x)

and

\cos(x)

are shown below.

SineTaylor