Yang Hui
Quick Info
Qiantang (now Hangzhou), Chekiang province, China
China
Biography
Little is known about Yang Hui other than that he wrote several outstanding mathematical texts. He was a contemporary of both Qin Jiushao and Li Zhi, which we know from the dates on which his texts appeared, showing that he lived towards the end of the Nan (Southern) Sung dynasty. However, both Qin and Li's major works appeared about fifteen years before the first work of Yang. Zhu Shijie was only born about the time Yang Hui's first texts were appearing so his life also overlapped that of Yang.There is a small amount of information about Yang Hui which he relates in his books. He tells us that he was taught mathematics by Liu I who was a native of Chung-shan, in Kwangtung province, which is south of Chekiang province where Yang Hui was born. Nothing at all is known of Liu I, so this information is less helpful in giving us details of Yang Hui than it might be. Again we know the names of four of Yang's friends who were also interested in mathematics, but again as these men are unknown except for Yang's reference to them. The best guess that historians make is that Yang was a minor Chinese official. Most Chinese scholars of the period were officials, for there were no professional mathematicians, but he could not have held an important post since were he a major official he would appear in records of the dynasty. I [EFR] am less certain about this standard view.
I base my argument on the style and content of Yang's books, for it is clear from these that he was an experienced teacher. More than this, he is writing as a teacher trying to find the most interesting and helpful explanation. Any teacher of mathematics today can identify with what Yang is trying to do here. Of course, this in no way proves that the view of Yang as a minor official is false, indeed he could be an official with responsibility for teaching mathematics, but I suggest that it is more likely that he was an active teacher of mathematics who would have had a group of young students around him.
In 1261 Yang wrote the Xiangjie jiuzhang suanfa (Detailed analysis of the mathematical rules in the Nine Chapters and their reclassifications). He tells us that he had obtained a fine edition of the Nine Chapters on the Mathematical Art which contained notes by Jia Xian on the edition commented on by Liu Hui and later by Li Chunfeng. The notes by Jia Xian have not survived so we know of them only through the references from Yang. What Yang produced was not intended to be a further commentary on the ancient classic but instead he selected 80 of the 246 problems for his discussion. He chose these 80 since he felt that they were representatives of the different techniques which were presented in the Nine Chapters.
Yang's Detailed analysis contained twelve chapters. Nine of the twelve correspond to those of the Nine Chapters but there are three further chapters: one containing geometrical figures, one containing the fundamental methods, and one in which Yang presents a new classification of the problems. Each problem is studied by Yang for three different aspects. Firstly he explains the logic behind the problem, secondly he gives a numerical solution to the problem, and thirdly he shows how the method he has presented can be modified to solve similar problems. For example, if the problem reduced to the solution of a quadratic equation, then Yang would solve it numerically, then show how to solve a general quadratic equation numerically.
Problem 16 in Chapter 7 of the Nine Chapters is as follows:-
Now 1 cubic cun of jade weighs 7 liang, and 1 cubic cun of rock weighs 6 liang. Now there is a cube of side 3 cun consisting of a mixture of jade and rock which weighs 11 jin. Tell: what are the weights of jade and rock in the cube. [Note 1 jin = 16 liang]If there are cubic cun of jade and cubic cun of rock in the cube then
Although Yang has presented a problem straight from the Nine Chapters his method of solution is quite different. What Yang's method essentially reduces to is finding the determinant of the matrix of coefficients of the system of equations. Of course he gets the same answer as the earlier authors and commentators, namely that the cube contains 14 cubic cun of jade weighing 6 jin 2 liang, and 13 cubic cun of rock weighing 4 jin 14 liang.
There is other work in Yang's Detailed analysis that we should single out for a mention. He gives what today is called Pascal's triangle, up to the sixth row, saying that he learnt it from Jia Xian's treatise. Yang also gave formulae for the sum of certain series, for example he found the sum of the squares of the natural numbers from to and showed that
.
See [14] for a discussion of the geometrical ideas which lie behind Yang's approach to summing series.
A year after producing Detailed analysis Yang wrote Riyong suanfa (Mathematics for everyday use). Although the text of this has been lost, we know enough about it from quotes in other works to know that it was an elementary text. Yang says that he wrote it:-
... to assist the reader with the numerous matters of daily use and also to instruct the young in observation and practice.In [19] some of the quotes which allow a partial reconstruction of this work are translated into English. In his text Yang explained:-
... the additive method of multiplication and the subtractive method of division [relative to the] ten problems and their solutions.Over the next years Yang must have continued to produce material for mathematics texts but he published nothing more until 1274 when Cheng Chu Tong Bian Ben Mo which means Alpha and omega of variations on multiplication and division appeared. This was a three chapter work, each chapter having its own title. The first chapter is Fundamental changes in calculation, the second is Computational treasure for variations in multiplications and divisions, and the third, written in collaboration with Shih Chung-yung who was one of his friends, is Fundamentals of the applications of mathematics.
In 1275 two further works by Yang appeared; the Practical mathematical rules for surveying and Continuation of ancient mathematical methods for elucidating strange properties of numbers, both being works of two chapters. All Yang's volumes of 1274 and 1275 were assembled into what were essentially his collected works called Yang Hui suanfa (Yang Hui's methods of computation). An English translation of the Yang Hui suanfa appears in [3]. The topics covered by Yang include multiplication, division, root-extraction, quadratic and simultaneous equations, series, computations of areas of a rectangle, a trapezium, a circle, and other figures. He also gives a wonderful account of magic squares and magic circles which we give more information about below.
One of the more remarkable aspects of this work is the document on mathematics education Xi Suan Gang Mu (A syllabus of mathematics) which prefaced the first chapter of Cheng Chu Tong Bian Ben Mo. Man Keung Siu, reviewing [10], writes that the syllabus:-
... is an important and unusual extant document in mathematics education in ancient China. Not only does it specify the content and the time-table of a comprehensive study program in mathematics, it also explains the rationale behind the design of such a curriculum. It emphasizes a systematic and coherent program that is based on real understanding rather than on rote learning. This program is a marked improvement on the traditional way of learning mathematics by which a student is assigned certain classical texts, to be studied one followed by the other, each for a period of one to two years!The syllabus is a fascinating document for it shows Yang's concern that mathematics is properly taught to those meeting the subject for the first time. This was not the first time Yang had shown such concerns, for his elementary text of 1262 was also clearly designed to help beginners.
Here is a problem taken from Chapter 2 of Continuation of ancient mathematical methods for elucidating strange properties of numbers.
100 coins buy Wenzhou oranges, green oranges, and golden oranges, 100 in total. If a Wenzhou orange costs 7 coins, a green orange 3 coins, and 3 golden oranges cost 1 coin, how many oranges of the three kinds will be bought?Yang's solution is quoted in [8]:-
From 3 times 100 coins subtract 100 coins; from 3 times the cost of a Wenzhou orange i.e. 21, subtract 1; the remainder is 20. From 3 times the cost of a green orange, i.e. 9, subtract 1; the remainder is 8. The sum of the remainder is 28. Divide 200 by 28, we have the integer 6. These are the numbers to be found; 6 Wenzhou oranges and 6 green oranges respectively. And then (200 - 6 × 28) ÷ 8 = 4, this is the difference of the number of Wenzhou oranges and green oranges. Hence the sum of them is 16, whereas the number of gold oranges to be found is 84.What is Yang doing? At first sight it seems to make no sense, so let us look at how we might approach such a problem. Suppose there are Wenzhou oranges, green oranges and golden oranges. Then a modern solution would set up equations
Multiplying the second by 3 and putting it first gives
Now look at Yang's explanation. He is subtracting the second equation from the first: 300 - 100 coins, 21 - 1 Wenzhou oranges, 9 - 1 green oranges. He gets
Then let , say, be the difference of the number of Wenzhou oranges and green oranges, so . Look at Yang's explanation. This is exactly what he is doing! Replace in the above equation so that
so
giving
.
Hence and 100 - (6 + 10) = 84 which is the number of golden oranges.
If you want to try one of Yang's problems, here is another of the same type, being the first problem in Chapter 2:-
A number of pheasants and rabbits are placed together in the same cage. Thirty-five heads and ninety-four feet are counted. Find the number of pheasants and rabbits.Finally let us note Yang's remarkable contribution to magic squares. Firstly it is important to realise that he presents them as a good way to interest people in numbers, and he does not claim any magic properties. We have used the standard term magic square, but Yang does not use the word magic, simply calling them number diagrams. He gives a magic square of order 3, two squares of order 4, two squares of order 5, two squares of order six, two squares of order 7, two of order 8, one of order nine, and one of order 10.
Yang's 3 × 3 square
 One of Yang's 4 × 4 squares
One of Yang's 4 × 4 squares 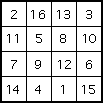
One of Yang's 5 × 5 squares
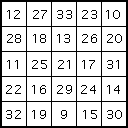 One of Yang's 6 × 6 squares
One of Yang's 6 × 6 squares 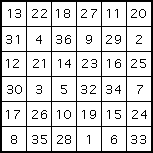
One of Yangs 7 × 7 squares is at THIS LINK.
One of Yangs 8 × 8 squares is at THIS LINK.
Yangs 9 × 9 square is at THIS LINK.
Yangs 10 × 10 square is at THIS LINK.
Again Yang does not claim any originality here, and writes as if he is presenting well known facts. This said, no record of the higher order magic squares now exist in the writings of earlier Chinese mathematicians.
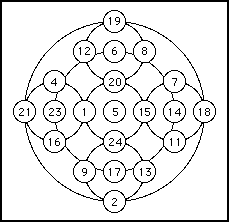
As a final arithmetical treat we give Yang's simplest magic circle.
The property to note here is that there are seven intersecting circles in the diagram. Each circle has a central number and four other numbers, in the north, south, east and west positions, on its circumference. Adding the central number and the four numbers on the circumference gives 65 for each of the seven circles.
References (show)
- H Peng-Yoke, Biography in Dictionary of Scientific Biography (New York 1970-1990).
See THIS LINK. - L Y Lam, A critical study of the 'Yang Hui suan fa': a thirteenth-century Chinese mathematical treatise (Singapore, 1977).
- Lay Yong Lam, A Critical Study of the Yang Hui Suan Fa: A Thirteenth-Century Chinese Mathematical Treatise, translated from Chinese (1977).
- J-C Martzloff, A history of Chinese mathematics (Berlin-Heidelberg, 1997).
- J-C Martzloff, Histoire des mathématiques chinoises (Paris, 1987).
- Y Mikami, Mathematics in China and Japan (New York, 1961).
- J Needham, Science and Civilisation in China III (Cambridge, 1959).
- K Shen, J N Crossley and A W-C Lun, The nine chapters on the mathematical art : Companion and commentary (Beijing, 1999).
- G C Smith, S Radvansky and M Chiba, History of mathematics and related sciences : an annotated bibliography of sources held by Monash University Library (Clayton, 1992).
- G Abe, Magic squares that occur in Yang-Hui's mathematics (Japanese), Sugakushi Kenkyu 70 (1976), 11-32.
- A Hirayama, The year in which Takakazu Seki copied the 'Yang Hui Suanfa' (Japanese), Sugakushi Kenkyu 68 (1976), 1-2.
- J Needham, Yang Hui and the coming of Euclid, in J Needham, Science and civilisation in China Vol. 3 : Mathematics and the sciences of the heavens and the earth (New York, 1959), Chapter 6.
- A E Raik, The calculation of some volumes in the Old Chinese treatise 'Mathematics in nine books' (Russian), Istor.-Mat. Issled. No. 14 (1961), 467-472.
- M K Siu, Pyramid, pile, and sum of squares, Historia Math. 8 (1) (1981), 61-66.
- K Q Sun, Hui Yang's triangle and determinant (Chinese), Sichuan Shifan Daxue Xuebao Ziran Kexue Ban 17 (4) (1994), 53-57.
- H A Sun, A note on computation of the area of a quadrilateral with different sides (Chinese), J. Liaoning Norm. Univ. Nat. Sci. 25 (3) (2002), 229-232.
- Yen Tun-chieh, A study of the mathematical books written by Yang Hui in the Sung period, in Discourses on the history of mathematics of the Sung and Yuan period (Peking 1966).
- L Y Yong, Yang Hui's commentary on the 'ying nu' chapter of the Chiu chang suan shu, Historia Math. 1 (1) (1974), 47-64.
- L Y Yong, The Jih yung suan fa: an elementary arithmetic textbook of the thirteenth century, Isis 63 (218) (1972), 370-383.
- A P Yushkevich, Studies in the history of mathematics in ancient China (Russian), Voprosy Istor. Estestvoznan. i Tekhn. (3) (1982), 125-136.
- A P Youschkevitch, Nouvelles recherches sur l'histoire des mathématiques chinoises, Rev. Histoire Sci. Appl. 35 (2) (1982), 97-110.
- L Y Yong, Yang Hui's commentary on the 'ying nu' chapter of the 'Chiu chang suan shu', Historia Math. 1 (1) (1974), 47-64.
- D M Zhou, 'A syllabus of mathematics' and Hui Yang's methodology of teaching mathematics (Chinese), J. Central China Normal Univ. Natur. Sci. 24 (3) (1990), 396-399.
Additional Resources (show)
Other pages about Yang Hui:
Other websites about Yang Hui:
Cross-references (show)
Written by J J O'Connor and E F Robertson
Last Update December 2003
Last Update December 2003
