Curves
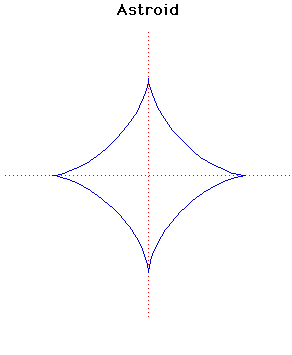
Astroid
Description
The astroid was first discussed by Johann Bernoulli in 1691-92. It also appears in Leibniz's correspondence of 1715. It is sometimes called the tetracuspid for the obvious reason that it has four cusps.The astroid only acquired its present name in 1836 in a book published in Vienna. It has been known by various names in the literature, even after 1836, including cubocycloid and paracycle.
The length of the astroid is and its area is .
The gradient of the tangent from the point with parameter is . The equation of this tangent is
Let cut the -axis and the -axis at and respectively. Then the length is a constant and is equal to .
It can be formed by rolling a circle of radius on the inside of a circle of radius .
It can also be formed as the envelope produced when a line segment is moved with each end on one of a pair of perpendicular axes. It is therefore a glissette.
Other Web site:
Xah Lee