Curves
Cartesian Oval
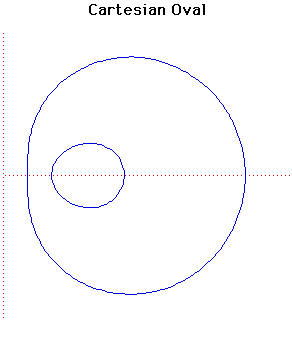
- Cartesian equation:
Description
This curve consists of two ovals so it should really be called Cartesian Ovals. It is the locus of a point whose distances and from two fixed points and satisfy . When is the distance between and then the curve can be expressed in the form given above.The curves were first studied by Descartes in 1637 and are sometimes called the 'Ovals of Descartes'.
The curve was also studied by Newton in his classification of cubic curves.
The Cartesian Oval has bipolar equation .
If then the Cartesian Oval is a central conic while if then the curve is a Limacon of Pascal (Étienne Pascal). In this case the inside oval touches the outside one.
Cartesian Ovals are anallagmatic curves.