Curves
Conchoid
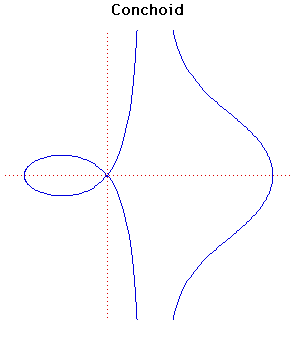
Description
The name means shell form and was studied by the Greek mathematician Nicomedes in about 200 BC in relation to the problem of duplication of the cube. Nicomedes recognised the three distinct forms seen in this family.Nicomedes was a minor geometer who worked around 180 BC. His main invention was the conchoid ascribed to him by Pappus. It was a favourite with 17 Century mathematicians and could be used, as Nicomedes had intended, to solve the problems of duplicating the cube and trisecting an angle.
Newton said it should be a 'standard' curve.
The conchoid has as an asymptote and the area between either branch and the asymptote is infinite. The area of the loop is
.
The conchoid was used in the construction of ancient buildings. The vertical section of columns was made in the shape of the loop of the conchoid.
Other Web sites:
Xah Lee