MacTutor logo MacTutor

Curves

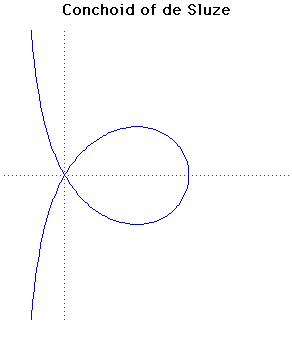
Conchoid of de Sluze

Main
Cartesian equation:
a(x+a)(x2+y2)=k2x2a(x + a)(x^{2} + y^{2}) = k^{2}x^{2}
Polar equation:
a(rcos⁡(θ)+a)=k2cos⁡2(θ)a(r \cos( \theta ) + a) = k^{2}\cos^{2}( \theta )

View the interactive version of this curve.

Description

This curve was first constructed by René de Sluze in 1662.

René Francois Walter- Baron de Sluze was an important man in the church as well as a mathematician. He contributed to the geometry of spirals and the finding of geometric means. He also invented a general method for determining points of inflection of a curve.

Associated Curves

Definitions of the Associated curves

  • Evolute
  • Involute 1
  • Involute 2
  • Inverse curve wrt origin
  • Inverse wrt another circle
  • Pedal curve wrt origin
  • Pedal wrt another point
  • Negative pedal curve wrt origin
  • Negative pedal wrt another point
  • Caustic wrt horizontal rays
  • Caustic curve wrt another point