MacTutor logo MacTutor

Curves

Devil's Curve

Main
Cartesian equation:
y4−x4+ay2+bx2=0y^{4} - x^{4} + a y^{2} + b x^{2} = 0
Polar equation
r=√[(25−24tan⁡2(θ))/(1−tan⁡2(θ))]r = √[(25 - 24\tan^{2}( \theta ))/(1 - \tan^{2}( \theta ))]

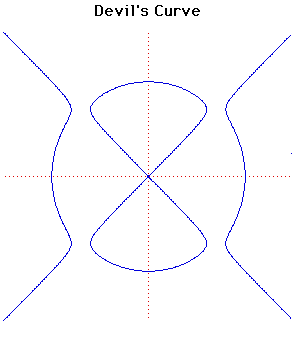
View the interactive version of this curve.

Description

The Devil's Curve was studied by Gabriel Cramer in 1750 and Lacroix in 1810. It appears in Nouvelles Annalesin 1858.

Cramer (1704-1752) was a Swiss mathematician. He became professor of mathematics at Geneva and wrote on work related to physics; also on geometry and the history of mathematics. He is best known for his work on determinants (1750) but also made contributions to the study of algebraic curves (1750).

Associated Curves

Definitions of the Associated curves

  • Evolute
  • Involute 1
  • Involute 2
  • Inverse curve wrt origin
  • Inverse wrt another circle
  • Pedal curve wrt origin
  • Pedal wrt another point
  • Negative pedal curve wrt origin
  • Negative pedal wrt another point
  • Caustic wrt horizontal rays
  • Caustic curve wrt another point