Curves

Durer's Shell Curves

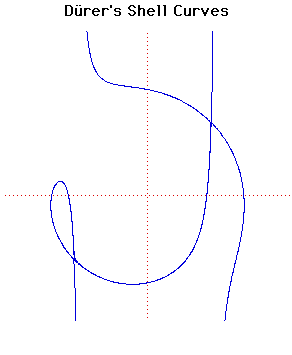
Cartesian equation:: $(x^{2} + xy + ax - b^{2})^{2} = (b^{2} - x^{2})(x - y + a)^{2}$

Description

These curves appear in Dürer's work Instruction in measurement with compasses and straight edge(1525).

Dürer calls the curve 'ein muschellini' which means a conchoid, but since it is not a true conchoid we have called it Dürer's shell curve (muschellini = conchoid = shell).

This curve arose from Dürer's work on perspective. He constructed the curve in the following way. He drew lines

QRP

and

P'QR

of length 16 units through

Q (q, 0)

and

R (0, r)

where

q + r = 13

. The locus of

P

and

P'

Q

and

R

move on the axes is the curve. Dürer only found one of the two branches of the curve.

The envelope of the line

P'QRP

is a parabola and the curve is therefore a glissette of a point on a line segment sliding between a parabola and one of its tangents.

There are a number of interesting special cases:
In the above formula we have:

b = 0

: Curve becomes two coincident straight lines

x^{2} = 0

a = 0

: Curve becomes the line pair

x = b/√2, x = -b/√2

together with the circle

x^{2} + y^{2} = b^{2}

a = b/2

: The curve has a cusp at

(-2a, a)

Associated Curves

Definitions of the Associated curves