Curves
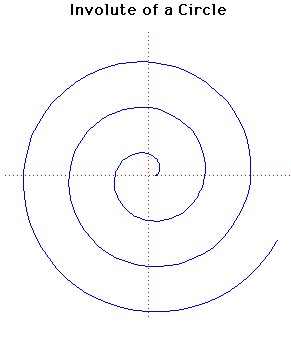
Involute of a Circle
Description
The involute of a circle is the path traced out by a point on a straight line that rolls around a circle.It was studied by Huygens when he was considering clocks without pendulums that might be used on ships at sea. He used the involute of a circle in his first pendulum clock in an attempt to force the pendulum to swing in the path of a cycloid.
Finding a clock which would keep accurate time at sea was a major problem and many years were spent looking for a solution. The problem was of vital importance since if GMT was known from a clock then, since local time could be easily computed from the Sun, longitude could be easily computed.
The pedal of the involute of a circle, with the centre as pedal point, is a Spiral of Archimedes.
Of course the evolute of an involute of a circle is a circle.