Curves
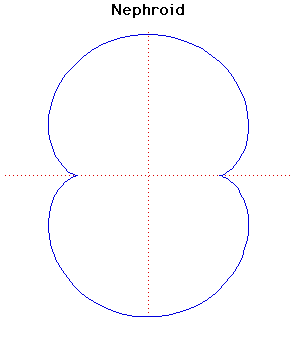
Nephroid
Description
The name nephroid (meaning 'kidney shaped') was used for the two-cusped epicycloid by Proctor in 1878. The nephroid is the epicycloid formed by a circle of radius rolling externally on a fixed circle of radius .The nephroid has length and area .
Huygens, in 1678, showed that the nephroid is the catacaustic of a circle when the light source is at infinity. He published this in Traité de la lumièrein 1690. An explanation of why this should be was not discovered until the wave theory of light was used. Airy produced the theoretical proof in 1838.
R A Proctor was an English mathematician. He was born in 1837 and died in 1888. In 1878 he published The geometry of cycloidsin London.
The involute of the nephroid is Cayley's sextic or another nephroid since they are parallel curves. To see the nephroid as an involute of itself see Involute 2 above constructing the involute through the point where the nephroid cuts the -axis.
Other Web site:
Xah Lee