Curves
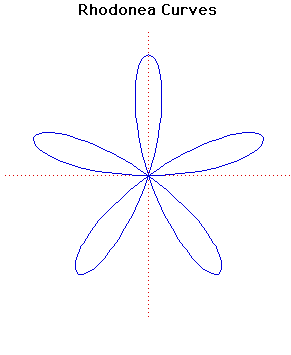
Rhodonea Curves
Description
These curves were named by the Italian mathematician Guido Grandi between 1723 and 1728 because they looked like roses.When is an integer there are or petals depending whether is odd or even. If is irrational then the number of petals is infinite.
The Quadrifolium is the rhodonea curve with . It has polar equation and cartesian form .
Luigi Guido Grandi was a member of the order of the Camaldolites. He became professor of philosophy in 1700 and professor of mathematics in 1714 both post being at the University of Pisa.
Grandi was the author of a number of works on geometry in which he considered the analogies of the circle and equilateral hyperbola. He also considered curves of double curvature on the sphere and the quadrature of parts of a spherical surface.
Other Web site:
Xah Lee