Curves
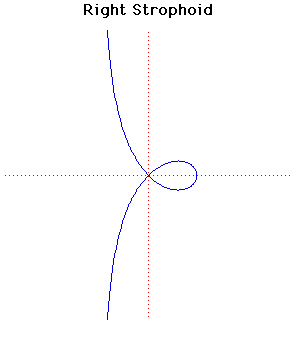
Right Strophoid
Description
The strophoid first appears in work by Isaac Barrow in 1670. However Torricelli describes the curve in his letters around 1645 and Roberval found it as the locus of the focus of the conic obtained when the plane cutting the cone rotates about the tangent at its vertex.The name (meaning a belt with a twist) was proposed by Montucci in 1846. The general strophoid has equation
.
The particular case of a right strophoid in where and the equation, in cartesians and polars, is that given above.
The area of the loop of the right strophoid is and the area between the curve and its asymptote is .
Let C be the circle with centre at the point where the right strophoid crosses the -axis and radius the distance of that point from the origin. Then the strophoid is invariant under inversion in the circle . Hence the strophoid is an anallagmatic curve.