Curves

Spiric Sections

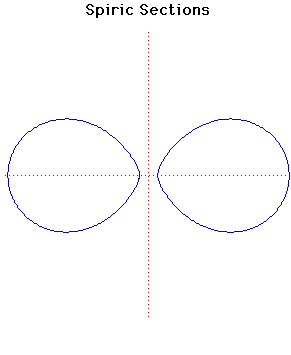
Cartesian equation:: $(r^{2} - a^{2} + c^{2} + x^{2} + y^{2})^{2} = 4r^{2}(x^{2} + c^{2})$

Description

After Menaechmus constructed conic sections by cutting a cone by a plane, around 150 BC which was 200 years later, the Greek mathematician Perseus investigated the curves obtained by cutting a torus by a plane which is parallel to the line through the centre of the hole of the torus.

In the formula of the curve given above the torus is formed from a circle of radius

a

whose centre is rotated along a circle of radius

r

. The value of

c

gives the distance of the cutting plane from the centre of the torus.

When

c = 0

the curve consists of two circles of radius

a

whose centres are at

(r, 0)

and

(-r, 0)

.

If

c = r + a

the curve consists of one point, namely the origin, while if

c > r + a

no point lies on the curve.

Associated Curves

Definitions of the Associated curves