Curves
Trisectrix of Maclaurin
Description
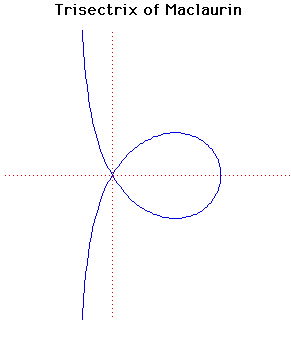
This was first studied by Colin Maclaurin in 1742. Like so many curves it was studied to provide a solution to one of the ancient Greek problems, this one is in relation to the problem of trisecting an angle. The name trisectrix arises since it can be used to trisect angles.The trisectrix of Maclaurin is an anallagmatic curve.
Another form of the equation is where the origin is inside the loop and the crossing point is on the negative -axis.
The tangents to the curve at the origin make angles of ± 60° with the -axis.
The area of the loop is and the distance from the origin to the point where the curve cuts the x-axis is .
It is the pedal curve of the parabola where the pedal-point is taken as the reflection of the focus in the directrix.
Other Web site:
Xah Lee