Curves
Watt's Curve
Description
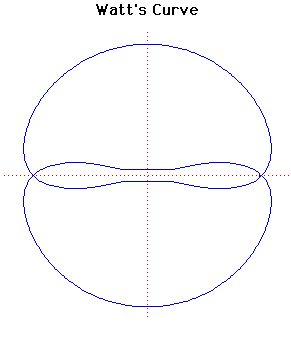
The curve is named after James Watt (1736- 1819), the Scottish engineer who developed the steam engine. In fact the curve comes from the linkages of rods connecting two wheels of equal diameter.Let two wheels of radius have their centres apart. Suppose that a rod of length is fixed at each end to the circumference of the two wheels. Let be the mid-point of the rod. Then Watt's curve is the locus of .
If then is a circle of radius with a figure of eight inside it.
Sylvester, Kempe and Cayley further developed the geometry associated with the theory of linkages in the 1870's. In fact Kempe proved that every finite segment of an algebraic curve can be generated can be generated by a linkage in this way.