Curves
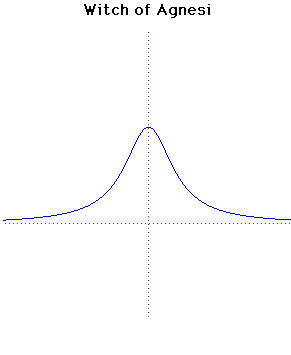
Witch of Agnesi
Description
This was studied and named versiera by Maria Agnesi in 1748 in her book Istituzioni Analitiche. It is also known as Cubique d'Agnesi or Agnésienne. There is a discussion on how it came to be called witch in Agnesi's biography.The curve had been studied earlier by Fermat and Guido Grandi in 1703.
The curve lies between and . It has points of inflection at . The line is an asymptote to the curve.
The curve can be considered as the locus of a point defined as follows. Draw a circle with centre at through . Draw a line from cutting at and the line at . Then has the -coordinate of and the -coordinate of .
The tangent to the Witch of Agnesi at the point with parameter is
.
Other Web site:
Xah Lee