Using a computer to visualise change in biological organisms
In his pioneering work On Growth and Form published in 1917, the biologist D'Arcy Thompson (1860 - 1948) laid the foundations of what is now called bio-mathematics.
Here is a picture of D'Arcy Thompson. You can see more about him at THIS LINK.

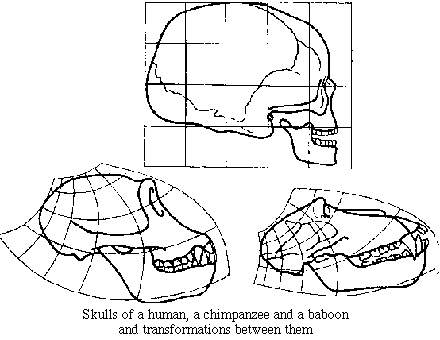
D'Arcy Thompson considered how mathematical functions could be applied to pictures of one living organism to transform them into others. Among his most striking examples are the use of linear and non-linear functions to, for example, alter pictures of baboon skulls into skulls of other primates or humans, to transform the profiles of various fishes into one another, as well as showing how the corresponding bones (shoulder blades for example) in different species were related.
The picture below shows a pair of pictures from On Growth and Form of species of fish and the way that a transformation of the plane can move one into the other.
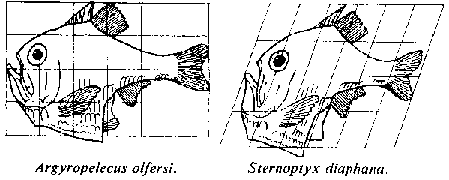
We have implemented some of these ideas by allowing users to alter pictures in real time by varying parameters in mathematical functions and seeing the pictures alter "before their eyes". This allows much greater flexibility than D'Arcy Thompson was able to achieve, since he was forced to do his transformations laboriously by hand.
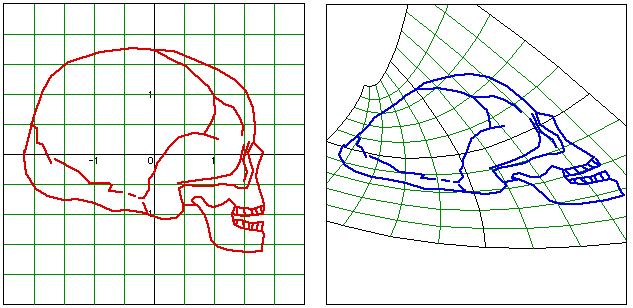
The picture below shows the user interface with an example corresponding to the D'Arcy Thompson pictures above. The red picture in the left-hand square is mapped to the blue image in the right hand square by the map defined at the bottom. The user can alter the parameters in the two functions which define the transformation by pressing the buttons below them and see the picture change continuously. The rate at which the parameters change can be varied, as can the range of the x and y values and the thickness of the lines used in the drawing. The user can choose whether the green lines showing the image of the grid are plotted.
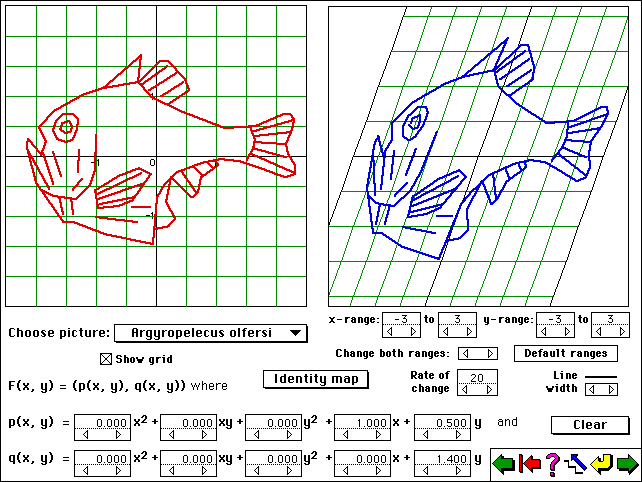
This last example used a linear map to effect the transformation (in which only the coefficients of x and y in the functions are non-zero). Playing with these linear maps by varying these four coefficients gives a good beginning to developing a feel for how such transformations act on the plane.
Although D'Arcy Thompson used a wide variety of transformations, we have experimented to show that most of his affects can be achieved by quadratic maps from the plane to itself. That is, maps of the form f(x,y) = (p(x,y), q(x,y)) where p and q are polynomials of degree 2 in two variables. This means that the user has the freedom to vary 10 parameters.
The two pictures below show another of D'Arcy Thompson's pair of fishes and how, although the map he evidently used is not a quadratic map, the use of a quadratic map can achieve much the same effect.
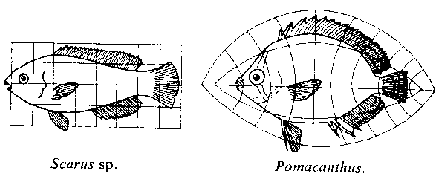
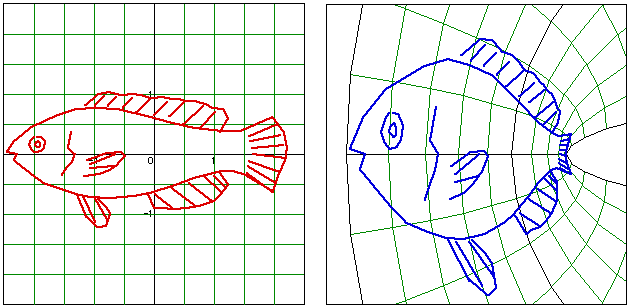
Using quadratic maps, when one is working with so many degrees of freedom, the ability to vary the parameters continuously and see the results of such variation, is vital to keep control of how the picture is changing. Since one believes that the way natural selection has worked to produce changes in organisms, is in this continuous fashion, it is very satisfying to feel that one has the ability to transform things in the same sort of way.
Some other pictures from On Growth and Form and the corresponding images from our project are shown below.
One set of images used by D'Arcy Thompson was taken from the artist (and mathematician) Albrecht Dürer's treatise on proportion: De Symetria Partium in Rectis Formis Humanorum Corporum Libri... published in Nuremberg after his death in 1528. One can amuse oneself by altering this image using a variety of linear and quadratic transformations. D'Arcy Thompson has an extensive discussion of the ideas of facial angle associated with this example.


As well as pre-loaded images (some from On Growth and Form and some from elsewhere) the user can use the mouse to make free-hand drawings in the left square. The computer will draw the images in the right-hand one and the user can then use the same method as before to watch these images change continuously. We have also included facilities for the user to import any images into our HyperCard stack, where they can then be digitised and explored in the same way as the ones we have provided.
We believe that this application of interactive computer technology offers insights into biological processes which are not achievable in other ways. It also gives an excellent way of persuading students of life-sciences that computer visualisation has a valuable part to play in understanding how living forms can evolve.
D'Arcy Thompson held a professorial chair here in St Andrews (and in Dundee) in Scotland for a record-breaking period of 64 years. As well as his great academic reputation, he made something of a name for himself as a mild eccentric. Older people in the town can still remember him walking around the streets of St Andrews with his parrot on his shoulder. The photograph below, showing D'Arcy Thompson (with his parrot) was taken outside an ice-cream parlour in St Andrews in the 1940's by the aunt of one of the authors.

It gives us particular satisfaction to feel that this project is continuing, in a small way, work originally started many years ago in St Andrews.
Here is a picture of D'Arcy Thompson. You can see more about him at THIS LINK.

D'Arcy Thompson considered how mathematical functions could be applied to pictures of one living organism to transform them into others. Among his most striking examples are the use of linear and non-linear functions to, for example, alter pictures of baboon skulls into skulls of other primates or humans, to transform the profiles of various fishes into one another, as well as showing how the corresponding bones (shoulder blades for example) in different species were related.
The picture below shows a pair of pictures from On Growth and Form of species of fish and the way that a transformation of the plane can move one into the other.

We have implemented some of these ideas by allowing users to alter pictures in real time by varying parameters in mathematical functions and seeing the pictures alter "before their eyes". This allows much greater flexibility than D'Arcy Thompson was able to achieve, since he was forced to do his transformations laboriously by hand.
The picture below shows the user interface with an example corresponding to the D'Arcy Thompson pictures above. The red picture in the left-hand square is mapped to the blue image in the right hand square by the map defined at the bottom. The user can alter the parameters in the two functions which define the transformation by pressing the buttons below them and see the picture change continuously. The rate at which the parameters change can be varied, as can the range of the x and y values and the thickness of the lines used in the drawing. The user can choose whether the green lines showing the image of the grid are plotted.

This last example used a linear map to effect the transformation (in which only the coefficients of x and y in the functions are non-zero). Playing with these linear maps by varying these four coefficients gives a good beginning to developing a feel for how such transformations act on the plane.
Although D'Arcy Thompson used a wide variety of transformations, we have experimented to show that most of his affects can be achieved by quadratic maps from the plane to itself. That is, maps of the form f(x,y) = (p(x,y), q(x,y)) where p and q are polynomials of degree 2 in two variables. This means that the user has the freedom to vary 10 parameters.
The two pictures below show another of D'Arcy Thompson's pair of fishes and how, although the map he evidently used is not a quadratic map, the use of a quadratic map can achieve much the same effect.


Using quadratic maps, when one is working with so many degrees of freedom, the ability to vary the parameters continuously and see the results of such variation, is vital to keep control of how the picture is changing. Since one believes that the way natural selection has worked to produce changes in organisms, is in this continuous fashion, it is very satisfying to feel that one has the ability to transform things in the same sort of way.
Some other pictures from On Growth and Form and the corresponding images from our project are shown below.


One set of images used by D'Arcy Thompson was taken from the artist (and mathematician) Albrecht Dürer's treatise on proportion: De Symetria Partium in Rectis Formis Humanorum Corporum Libri... published in Nuremberg after his death in 1528. One can amuse oneself by altering this image using a variety of linear and quadratic transformations. D'Arcy Thompson has an extensive discussion of the ideas of facial angle associated with this example.


As well as pre-loaded images (some from On Growth and Form and some from elsewhere) the user can use the mouse to make free-hand drawings in the left square. The computer will draw the images in the right-hand one and the user can then use the same method as before to watch these images change continuously. We have also included facilities for the user to import any images into our HyperCard stack, where they can then be digitised and explored in the same way as the ones we have provided.
We believe that this application of interactive computer technology offers insights into biological processes which are not achievable in other ways. It also gives an excellent way of persuading students of life-sciences that computer visualisation has a valuable part to play in understanding how living forms can evolve.
D'Arcy Thompson held a professorial chair here in St Andrews (and in Dundee) in Scotland for a record-breaking period of 64 years. As well as his great academic reputation, he made something of a name for himself as a mild eccentric. Older people in the town can still remember him walking around the streets of St Andrews with his parrot on his shoulder. The photograph below, showing D'Arcy Thompson (with his parrot) was taken outside an ice-cream parlour in St Andrews in the 1940's by the aunt of one of the authors.

It gives us particular satisfaction to feel that this project is continuing, in a small way, work originally started many years ago in St Andrews.