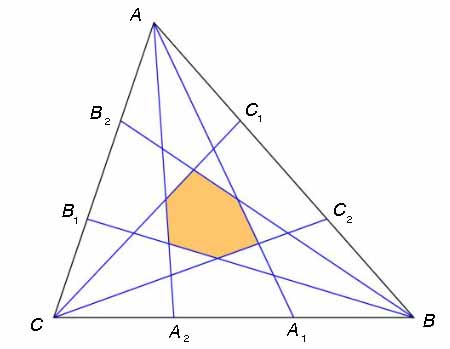

Let ABC be any triangle. Trisect each side, so that AB has C1 and C2 as the two trisection points and similarly for the other two sides. Draw the lines AA1, AA2, BB1, BB2, CC1, CC2. These lines define an hexagonal region in the middle of triangle ABC. Then the area of the hexagonal region is 1/10 the area of ABC.