Bell number diagrams

For example, the set {1, 2, 3} can be partitioned in the following ways:

• {{1}, {2}, {3}}
• {{1, 2}, {3}}
• {{1, 3}, {2}}
• {{1}, {2, 3}}
• {{1, 2, 3}}.

The n^th Bell number can be computed using the formula

,

represents the Stirling numbers of the second kind.

Here are some diagrams representing the different ways the sets can be partitioned: a line connects elements in the same subset, and a point represents a singleton subset.

(See below for Mathematica code to generate the lists of partitions.)

{1, 2, 3}, 5 partitions:

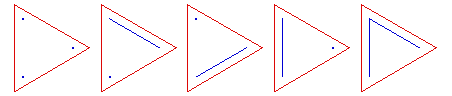
{1, 2, 3, 4}, 15 partitions:

{1, 2, 3, 4, 5}, 52 partitions:

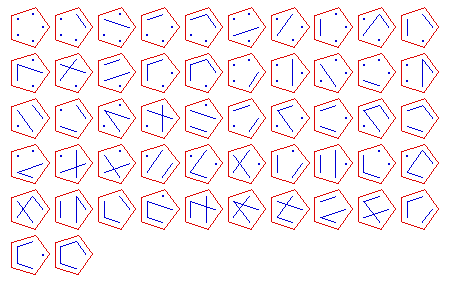
{1, 2, 3, 4, 5, 6}, 203 partitions:

{1, 2, 3, 4, 5, 6, 7}, 877 partitions:
(The GIF image is about 125K, so let me know if you're dying to see it.)

__________

Here's some Mathematica 3.0 code to generate the lists of Bell partitions. In short, the program computes lists of partitions recursively, using two cases. We compute BellList[n] by appending the singleton {n} to each element of BellList[n-1], and by appending the number n to each subset of each element in BellList[n-1]; this technique corresponds to the summation of the recurrence for Stirling numbers of the second kind:

.

BellList[1] = {{{1}}}; (* the basic case *)

BellList[n_Integer?Positive] := BellList[n] = (* do some caching *)

    Flatten[
      Join[
        Map[ReplaceList[#,{S__}->{S,{n}}]&, BellList[n-1]],

        Map[ReplaceList[#,{b___,{S__},a___}->{b,{S,n},a}]&, BellList[n-1]]],
      1]

BellList[2]//ColumnForm

{{1}, {2}}
{{1, 2}}


BellList[3]//ColumnForm

{{1}, {2}, {3}}
{{1, 2}, {3}}
{{1, 3}, {2}}
{{1}, {2, 3}}
{{1, 2, 3}}


BellList[4]//ColumnForm

{{1}, {2}, {3}, {4}}
{{1, 2}, {3}, {4}}
{{1, 3}, {2}, {4}}
{{1}, {2, 3}, {4}}
{{1, 2, 3}, {4}}
{{1, 4}, {2}, {3}}
{{1}, {2, 4}, {3}}
{{1}, {2}, {3, 4}}
{{1, 2, 4}, {3}}
{{1, 2}, {3, 4}}
{{1, 3, 4}, {2}}
{{1, 3}, {2, 4}}
{{1, 4}, {2, 3}}
{{1}, {2, 3, 4}}
{{1, 2, 3, 4}}

Back to Stirling
Back to Bell