Zhukovsky (or Jowkowski) aerofoils
Zhukovsky's transformation is the map from to given by (or more generally ).
It was studied by Zhukovsky because the image of a circle which passes through the point z = 1 or z = -1 is a curve similar to the cross-section of an aircraft wing or propeller.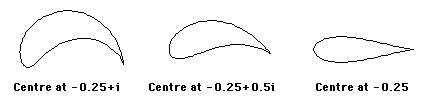
One of the curious and useful facts about differentiable complex functions is that their real and imaginary parts satisfy Laplace's Equation (a partial differential equation important in many applications from Electricity to Hydrodynamics).
Composing with Zhukovsky's function allows one to take the symmetric flow of fluid past a circular cylinder and transform it into the unsymmetric flow past such an aerofoil. One can then calculate the characteristics of such a flow.
It was studied by Zhukovsky because the image of a circle which passes through the point z = 1 or z = -1 is a curve similar to the cross-section of an aircraft wing or propeller.
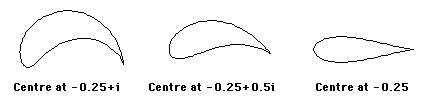
One of the curious and useful facts about differentiable complex functions is that their real and imaginary parts satisfy Laplace's Equation (a partial differential equation important in many applications from Electricity to Hydrodynamics).
Composing with Zhukovsky's function allows one to take the symmetric flow of fluid past a circular cylinder and transform it into the unsymmetric flow past such an aerofoil. One can then calculate the characteristics of such a flow.
Last Updated May 2000