Bell number diagrams
The Bell numbers
The nth Bell number can be computed using the formula
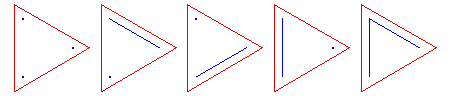
Here are some diagrams representing the different ways the sets can be partitioned: a line connects elements in the same subset, and a point represents a singleton subset.
{1, 2, 3}, 5 partitions:
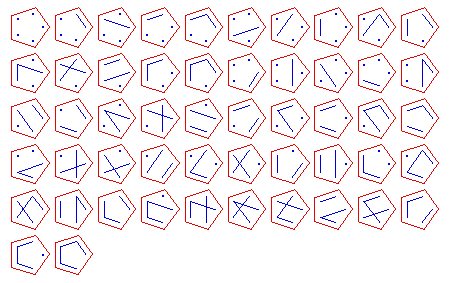
{1, 2, 3, 4}, 15 partitions:

{1, 2, 3, 4, 5}, 52 partitions:
{1, 2, 3, 4, 5, 6}, 203 partitions:

{1, 2, 3, 4, 5, 6, 7}, 877 partitions:
(The GIF image is about 125K, so let me know if you're dying to see it.)
Copyright © 1996 Robert M. Dickau
(1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, ...)
describe the number of ways a set with n elements can be partitioned into disjoint, non-empty subsets.For example, the set {1, 2, 3} can be partitioned in the following ways:
- {{1}, {2}, {3}}
- {{1, 2}, {3}}
- {{1, 3}, {2}}
- {{1}, {2, 3}}
- {{1, 2, 3}}.
The nth Bell number can be computed using the formula
where represents the Stirling numbers of the second kind.
Here are some diagrams representing the different ways the sets can be partitioned: a line connects elements in the same subset, and a point represents a singleton subset.
{1, 2, 3}, 5 partitions:

{1, 2, 3, 4}, 15 partitions:

{1, 2, 3, 4, 5}, 52 partitions:

{1, 2, 3, 4, 5, 6}, 203 partitions:

{1, 2, 3, 4, 5, 6, 7}, 877 partitions:
(The GIF image is about 125K, so let me know if you're dying to see it.)
Copyright © 1996 Robert M. Dickau