1.1.1 Johann Bernoulli, Opera omnia, tam antea sparsim edita (1742).

Virtually all of Bernoulli's work was published in journals. This first edition of Johann Bernoulli's collected works, which he supervised himself, brings together 189 of his papers and 59 of his lectures. Volume I is primarily devoted to problems in geometry and the early calculus, but also contains papers on mechanics, the resistance of solids, and a geometrical demonstration of the motion of pendulums and projectiles in resisting and unresisting media. Volumes II and III are almost totally devoted to problems of mechanics, the first of these containing his theoretical essay on the manoeuvring of vessels and related papers, as well as numerous contributions on the analysis of trajectories. His discourse on the laws governing the communication of movement opens Volume III, which also contains his essay on celestial mechanics. The final volume contains contributions on the curvature of elastic plates, his mechanico-dynamical propositions, and problems in dynamics. It had been Johann Bernoulli's plan to publish some of his letters in his Opera Omnia, and he sent hundreds of them to Gabriel Cramer, the editor. Of these, the 150 letters to and from Leibniz were published in 1745, but neither the publisher nor the editor Cramer could find resources for the rest. Most importantly this volume contains the first printing of the Hydraulica, which was written in competition with his son.

1.1.2 Vincenzo Riccati, Opusculorum ad res physicas & mathematicas pertinentium (1757).

Vincenzo Riccati taught mathematics in Bologna for thirty years at the College of St Francis Xavier. In this book, printed in Bologna, Riccati introduced the use of hyperbolic functions. Using hyperbolic functions he obtained the roots of certain types of algebraic equations, particularly cubic equations. He gave these functions the names "hyperbolic sine", "hyperbolic cosine", etc., by which they are known today, and he also introduced a notation for them (sh x, ch x, and so on) which is not used. The hyperbolic functions were also introduced, independently of Riccati, by the German mathematician Johann Heinrich Lambert in 1761 with the notation sinh x, cosh x, etc.

1.2.1 Geometria à Renato Des Cartes, Anno 1637 Gallicè edita; postea autem unà cum notis. Florimondi de Beaune, Francisci à Schooten (1659).

This edition of René Descartes' Geometry is by Florimond de Beaune and Frans van Schooten. Descartes first published his Geometry in Discours de la méthode (Leyde, 1637). This book by Florimond de Beaune and Frans van Schooten is the first separate edition of Descartes' Geometry.

1.2.2 Charles Bossut, Traité de calcul différentiel et de calcul intégral (1798).

This work is only of minor importance and was never reprinted. Bossut wrote it shortly before Lagrange presented a much more rigorous approach to the differential and integral calculus. Bossut writes in the Preface, "Citizen Lagrange has presented the metaphysics of the calculus under a new light, in his Théorie des fonctions algébriques; but I have obtained knowledge of this excellent work only after mine was completed and even largely printed."

1.2.3 Ruggero Boscovich, Elementorum Universae Matheseos (3 volumes) (1752-54).

This is the first edition of an important mathematical treatise by the physicist and astronomer Ruggero Giuseppe Boscovich (1711-1787), one of the first natural philosophers to spread Newtonian science in Italy. The work is divided into three volumes: Volume I contains Plane Geometry, Vulgar Arithmetic, Solid Geometry, Plane and Spherical Trigonometry; Volume II contains finite algebra; Volume III contains the elements of conic sections prepared by a new method and a dissertation on the transformation of geometrical spaces where you read about Continuity and about some Mysteries of the Infinite. The third volume in particular lays the mathematical foundations of Boscovich's most important work, the Philosophiae naturalis theoria redacta ad unicam legem virium in natura existentium.

1.2.4 Girolamo Saladini, Nuovo metodo delle proporzioni aritmetica, geometrica ed armonica (1761).

Girolamo Saladini (1735-1813) was born in Lucca. He was a pupil of Vincenzo Riccati and a collaboration between teacher and former student led to the joint work Institutiones analyticae, a treatise on mathematical analysis published in three volumes in Bologna in 1765-1767. Saladini taught higher mathematics at the University of Bologna giving, in particular, many courses on geometry and astronomy.

TABLE OF CONTENTS OF Saladini's Proporzioni.

DEDICATION: Signori Anziani e Gonfaloniero Di Giustzia.
PREFACE: Approval
CHAPTER: Article I. Of Geometric Proportion.
CHAPTER: Article II. Of Arithmetic Proportion.
CHAPTER: Article III. Of Harmonic Proportion.

1.3.1 Christoph Clavius, Opera Mathematica (1611-1612).

The Opera Mathematica of Christoph Clavius was compiled in 1611-1612 and contains works within the fields of both pure and applied mathematics. One of the most famous selections is, of course, Clavius's exposition of the Gregorian calendar. "He was considered an illustrious mathematician and astronomer; one to whom scholars and potentates would entrust with the most sensitive scientific problems of the day. Even so, he has yet to be given full credit for all of his scientific accomplishments."

1.3.2 Christoph Clavius, Euclidis elementorum (1574).

Clavius prepared this edition of Euclid's Elements for his students at the Rome College (Collegio Romano). Clavius's "Elements, which is not a translation of Euclid, contains a vast quantity of notes collected from previous commentators and editors, as well as some good criticisms and elucidations of his own. Among other things, Clavius made a new attempt at proving 'the postulate of the parallels.' In a scholium to the twelfth proposition of the ninth book of Euclid, Clavius objects to Cardan' claim to originality in employing a method that derives a proposition by assuming the contradictory of the proposition to be proved. According to Clavius, Cardan was anticipated in this method by Euclid and by Theodosius of Bithynia in the twelfth proposition of the first book of his Sphaericorum."

1.4.1 Claude Dechales, Cursus seu mundus mathematicus (4 volumes) (1674).

This book by Claude Dechales is a complete course of mathematics. Topics covered in this wide ranging work included practical geometry, mechanics, statics, magnetism and optics as well as topics not today considered to be among the usual topics of mathematics such as geography, architecture, astronomy, natural philosophy and music.The book was widely used but it is old-fashioned in its coverage. For example, in algebra it owes more to Diophantus than to the algebraists of its day.

Topics in Volume 1 include: Euclid Book XIV; Conic Sections; Arithmetic; Trigonometry; Algebra. Topics in Volume 2 include: Practical Geometry; Mechanics; Statics; Geography; Magnetism; Civil Architecture. Topics in Volume 3 include: Military Architecture; Hydrostatics; Fountains and Rivers; Hydraulics; Navigation; Optics; Perspective; Using a mirror to focus light; Refracting light. Topics in Volume 4 include: Music; Pyrotechnics; Astrolabe; Sundial; Astronomy; Astrology; Calendar.

1.4.2 Pietro Cossali, Scritti Inediti del P D Pietro Cossali: Chierico Regolare Teatino (1857).

These previously unpublished writings of Pietro Cossali were edited by the Italian historian of mathematics Prince Baldassarre Boncompagni-Ludovisi (1821-1894). There is also an appendix containing four letters addressed to the same Father Cossali and a note on these letters. Pietro Cossali (1748-1815) taught physics at the University of Parma from 1787 to 1805. Then, in 1805, he was named professor of higher calculus at the University of Padua by Napoleon Bonaparte. Cossali wrote Origine, transporto in Italia, primi progressi in essa dell'algebra (1799) which describes the work of Fibonacci and the emergence of algebra in Italy. It is considered the first text on the history of Italian mathematics.

TABLE OF CONTENTS OF Scritti Inediti del P D Pietro Cossali.

PREFACE: Preface.
CHAPTER ONE: On Leonardo Pisano.
CHAPTER TWO: On the book of Leonardo Pisano.
CHAPTER THREE: In praise of Fra Luca Pacioli.
CHAPTER FOUR: Extract from the Summa of Fra Luca.
CHAPTER FIVE: Notes on the general treatise of numbers and measures by Niccolò Tartaglia printed in Venice in the year 1556.
CHAPTER SIX: Lessons on arithmetic.
CHAPTER SEVEN: Historical-scientific memoirs.
APPENDIX: Appendix.

1.5.1 Carlo Bossut, Elementi d'Algebra e Geometria (1808).

Printed in Bologna, this is a two volume work translated from French to Italian by Francesco Cardinali (1779-1837). Cardinali translated the algebra and geometry from Bossut's Cours complet de Mathematiques. Cardinali wrote many works for educational use and he was a teacher of mathematics in the Liceo of Treviso for ten years. For more about Francesco Cardinali, see 1.5.4. below.

1.5.2 Ruggero Giuseppe Boscovich, Elementi di Matematiche Pure secondo il metodo del chiarissimo Signor Abbate De La Caille. Edizione seconda italiana. Accresciuta del Trattato della Trigonometria Sferica del Padre Ruggero Giuseppe Boscovich (1774).

Elements of Pure Mathematics according to the method of the illustrious Monsieur Abbate De Lacaille. Second Italian edition. Augmented by the Treatise on Spherical Trigonometry by Father Ruggero Giuseppe Boscovich.

1.5.3 Leonard Euler, Élémens d'algèbra avec des notes et des additions (1774).

This two volume work is a translation into French of the German edition of Euler's Elements of Algebra (1770). The translation was by Daniel Bernoulli, who was a friend and colleague of Euler. Élémens d'algèbra was written in numbered paragraphs as was the style of mathematics texts of that time. It begins with the definition of mathematics, then introduces the fundamental operations of arithmetic and number systems gradually building towards more abstract topics.

TABLE OF CONTENTS OF Élémens d'algèbra.

SECTION ONE. Of the different methods of calculation for simple or incomplex quantities.

CHAPTER I. On mathematics in general,
CHAPTER II. Explanation of the signs, plus and minus,
CHAPTER III. On the multiplication of simple quantities,
CHAPTER IV. On the nature of whole numbers, with respect to their factors,
CHAPTER V. On the division of simple quantities,
CHAPTER VI. On the properties of whole numbers in relation to their divisors,
CHAPTER VII. On fractions in general,
CHAPTER VIII. On the properties of fractions,
CHAPTER IX. On the addition and subtraction of fractions,
CHAPTER X. On the multiplication and division of fractions,
CHAPTER XI. On square numbers,
CHAPTER XII. On square roots and the irrational numbers resulting therefrom,
CHAPTER XIII. On impossible or imaginary quantities, which are derived from the same source,
CHAPTER XIV. On cubic numbers,
CHAPTER XV. On cubic roots and of irrational numbers derived therefrom,
CHAPTER XVI. On powers in general,
CHAPTER XVII. On the calculus of powers,
CHAPTER XVIII. On roots, relative to all powers in general,
CHAPTER XIX. On the manner of indicating irrational numbers by fractional exponents,
CHAPTER XX. On the different manners of calculating, and of their connection with each other,
CHAPTER XXI. On logarithms in general,
CHAPTER XXII. On the tables of logarithms in use,
CHAPTER XXIII. On the manner of representing logarithms.

SECTION TWO. On the different methods of calculation for composite or complex quantities.

CHAPTER I. On the addition of complex quantities,
CHAPTER II. On the subtraction of complex quantities,
CHAPTER III. On the multiplication of complex quantities,
CHAPTER IV. On the division of complex quantities,
CHAPTER V. On the resolution of fractions in infinite sequences,
CHAPTER VI. On the squares of complex quantities,
CHAPTER VII. On the extraction of roots applied to complex quant.,
CHAPTER VIII. On the calculation of irrational quantities,
CHAPTER IX. On cubes and the extraction of cubic roots,
CHAPTER X. On higher powers of complex quantities,
CHAPTER XI. On the permutation of letters,
CHAPTER XII. On the development of irrational powers by infinite sequences,
CHAPTER XIII. On the development of negative powers,

SECTION THREE. On ratios and proportions.

CHAPTER I. On the arithmetic ratio, or of the difference between two numbers,
CHAPTER II. On arithmetic proportions,
CHAPTER III. On arithmetic progressions,
CHAPTER IV. On the summation of arithmetic progressions,
CHAPTER V. On figurative numbers or polygons,
CHAPTER VI. On the geometric ratio,
CHAPTER VII. On the greatest common divisor of two given numbers,
CHAPTER VIII. On geometric proportions,
CHAPTER IX. Remarks on proportions & on their use,
CHAPTER X. On compound ratios,
CHAPTER XI. On geometric progressions,
CHAPTER XII. On infinite decimal fractions,
CHAPTER XIII. Interest calculations.

SECTION FOUR. On algebraic equations, and of the resolution of these equations.

CHAPTER I. On the resolution of problems in general,
CHAPTER II. On the resolution of equations of the first degree,
CHAPTER III. On the solution of some questions relating to the preceding chapter,
CHAPTER IV. On the resolution of two or more equations of the first degree,
CHAPTER V. On the resolution of pure equations of the second degree,
CHAPTER VI. On the resolution of mixed equations of the second degree,
CHAPTER VII. On the extraction of the roots of polygonal numbers,
CHAPTER VIII. On the extraction of the square roots of binomials,
CHAPTER IX. On the nature of equations of the second degree,
CHAPTER X. On pure equations of the third degree,
CHAPTER XI. On the resolution of complete equations of the third degree,
CHAPTER XII. On the rule of Cardan, or of Scipione Ferro,
CHAPTER XIII. On the resolution of equations of the fourth degree,
CHAPTER XIV. On the rule of Bombelli, to reduce the resolution of equations of the fourth degree to those of the third degree,
CHAPTER XV. On a new method of solving equations of the fourth degree,
CHAPTER XVI. On the resolution of equations by approximations,

End of Table.

1.5.4 Francesco Cardinali, Elementi d'aritmetica (1808).

Francesco Cardinali (Imola, 1779 - Rome, 1837) was a character with rather varied interests, who studied with equal attention both the scientific and the humanistic disciplines. In the first part of his life Cardinali was essentially a mathematician; when the alternating Italian political events prevented him from continuing this career, he attempted to enter the literary environment in the triple role of author, editor and printer.

During the first decade of the nineteenth century, in an attempt to obtain a university chair, Cardinali published a certain number of memoirs on analytical subjects: three of them concerned the examination of some types of differential equations, one of them on elliptic transcendents. In 1808 Cardinali obtained the chair of mathematics at the Liceo of Treviso. Two mathematical works of a didactic nature date back to this period: the Elementi d'aritmetica written for use in the municipal schools of higher arithmetic of the Kingdom of Italy and augmented with the new instruction in measures and weights of the Kingdom (Bologna, 1808). The second book is the one described in 1.5.1. above.

1.5.5 Nicolas Louis de Lacaille, Leçons Élémentaires De Mathématiques: Ou Élémens D'Algèbre Et De Géométrie (1744).

TABLE OF CONTENTS OF Leçons Élémentaires De Mathématiques.

General Idea of ​​Mathematics, and Definitions of the Principal Terms.
Principal Axioms.

PART ONE. Of Arithmetic.

On the Nature of Numbers, of their Formation, and of their Value.
On the Operations of Arithmetic.
On the Rules of Addition.
On Subtraction.
On the Other Operations of Arithmetic.
On Multiplication.
On Division.

Elements of Algebra.

Definitions of Some Terms Used in Algebra.
On Algebraic Operations.
On Reduction.
On Addition.
On Subtraction.
On Multiplication.
On Division.
On Fractions.
On the Nature of Fractions in General, of their Values ​​and of their Comparisons.
On the Arithmetic Operations Which Can Be Done on Fractions.
On the Reduction of Fractions.
On the Addition of Fractions.
On Subtraction.
On Multiplication.
On Division.
On Decimal Fractions.
On the Nature of Decimal Fractions.
On Operations on Decimal Fractions.
On Other Kinds of Fractions.
On the Composition and Decomp. of Quantities.
To Find All the Divisors of a Given Quantity.
To Extract the Root of a Given Quantity.
On the Extraction of the Cubic Root.
Calculation of Incommensurables.
Calculation of Radicals.
Calculation of Powers by their Exponents.
On Equations or Analysis.
On Transposition.
On Multiplication and Division.
On the Extraction of Roots.
On Substitution.
On the Resolution of Problems by Analysis.

GENERAL REMARK. On the Solution of Problems by Analysis.

REMARKS. On the Nature and Solution of Problems of the Second Degree.

On Problems Which Lead to an Equation of the Second Degree.
Applications of the preceding Remarks to some cases of Equations of the fourth degree.
On the Comparison of magnitudes.
Treatise on reasons; and proportions.
Properties of reasons, proportions and Arithmetic progressions.
General problem on Arithmetic Progressions.
On reasons, proportions and Geometric progressions.
On the properties of magnitude considered in infinity.

PART TWO. Elements of Geometry.

FIRST SECTION- Of lines.

Origin and general properties of lines.
Properties of straight lines.
Properties of straight lines in the position of one line with respect to another.
Properties of straight lines in the position of one with respect to two or more others, without enclosing a space.
On some properties of straight lines with respect to the circle.
Properties of straight lines which enclose a space.
On Triangles. Of the different species, and of the properties of Triangles.
On the comparison of Triangles.
On other Polygons.
Properties of Polygons in general.
Properties of symmetrical Polygons both with salient angles and with re-entrant angles.
Properties of regular Polygons.
Properties of the circle.
On proportional lines.
On the comparison of figures.

SECTION TWO. Of Surfaces.

On the contour of surfaces and of their comparisons.
On the measurement of surfaces and their comparisons.
Remarks on the quadrature of the circle.
Properties of plane surfaces or planes.

THIRD SECTION. Of Solids.

Origin and properties of solids produced by a rectilinear motion.
Origin and properties of solids produced by a circular motion.
On Polyhedra and their comparisons.
On the comparison of Solids.
On the measurement of the surfaces of each kind of Solids.
Comparisons of the surfaces of Solids.
On the measurement of the solidities of each kind of Solids.
On the comparison of the solidities of Solids.
On Rectilinear Trigonometry
For Right Triangles.
For Oblique Triangles.
On Logarithms. Of their nature and their uses.
Remarks on the use of Tables of Logarithms.
Rules for the solution of all the Problems of Trigonometry, both by natural numbers and by Logarithms or artificial numbers.
For Right Triangles.
For Oblique Triangles.

CONIC SECTIONS.

Preliminary notions on the nature of curves in general.
Conic sections in general
Properties of the Parabola.
Properties of the Ellipse.
Properties of the Hyperbola.
Comparisons and general properties of Conic Sections.

1.6.1 Giordano Vitale, Euclide restituto, ovvero gli antichi elementi geometrici ristaurati e facilitati da Vitale Giordano da Bitonto (1680).

This book by Giordano Vitale (1633-1711) is part of a trend to revise the classics of mathematics that, at that time time, had particular success. Giordano restored the overall structure of the Euclidean text, providing an edition that respects the order and succession of the original demonstrations. The work contains, in the commentary, the result he is most famous for today, namely a theorem on Saccheri quadrilaterals. It can be simply stated as follows: If three points on a straight line AB are equidistant from a given line then all points on AB are equidistant from the given line. It was at that time an important step in understanding the parallel postulate.

Vitale Giordani was one of the most appreciated mathematicians of his time. He moved to Rome to escape a criminal pursuit and devoted himself to mathematics. There he entered Christina of Sweden's literary circle and taught at the Academy of France in Rome. In 1685 he obtained the chair of mathematics at La Sapienza, the University in Rome. The Euclide restituto was supposed to be the first volume in a much larger work but the rest of the project was never completed.

1.6.2 Odoardo Gherli, Gli elementi teorico-pratici delle mathematiche pure (1770).

This seven volume work includes an algebra volume, namely Volume II. The third volume treats plane and solid geometry (with applications to surveying), plane and spherical trigonometry, as well as logarithmic tables. The final volume, Volume VII, contains a quotation from Lagrange in which he declares the book to be "the most complete course of mathematics" among those published up to that time. The author Odoardo Gherli (1730-1780) was a Dominican who was Professor of Theology at the University of Modena and Professor of Mathematics at the University of Pisa. Let us quote from the book to understand Gherli approach:-

Although Euclid's method has been and is still commonly adopted, because it never departs from the most rigorous geometrical method, the essential circumstance of which is to give the understanding exactness, rule, and precision, yet because it continually interrupts the order of things, to which, in my opinion, must be attributed the insuperable difficulties that most beginners encounter, I have thought it wise not to follow it, although without ever breaking the laws of demonstration, in order to make the path easier for those who would dedicate themselves to this sublime and necessary science; and by adopting (as others have practiced before now) the most obvious and natural method, by which from the simplest notions one passes to the theorems of greater difficulty, and by a continuous chain, so to speak, I have tried to remove the obscurity, and make easily accessible those propositions which in Euclid are the stumbling block to students, even if of more than average intelligence. It seemed to me that this would lead beginners along an easier and shorter path to the knowledge of the most hidden secrets of this science, and would succeed in curbing their natural instability and frivolity, which, with restless inconstancy, leads them to tire and become displeased with everything ...

1.7.1 Pietro Franchini, La Scienza Del Calcolo (1816).

Pietro Franchini (1768-1837) was a teacher at the seminary in Veroli. He participated in the studies on the decimal metric system in Paris. His Theory of Analysis (1792) is important, but his best-known work is a monumental History of Algebra (1827), published in Lucca.

The book La Scienza Del Calcolo examines Leibniz' binary system and duodecimal system, the doctrine of combinations and permutations, sums of series, exponential and hypergeometric series, and theoretical applications of the binomial formula.

1.7.2 Silvestre-François Lacroix, Traité élémentaire du calcul des probabilités (1816).

The following description is based on an article by Frank J Swetz and Victor J Katz. Lacroix taught at the Ecόle Polytechnique, where he assisted Monge in producing his book on descriptive geometry. He later became a Professor of Mathematics at the Collège de France. Lacroix produced textbooks based on his lecture notes. These books were well received and their style and form were emulated by other European textbook writers of this period. Let us give one example of an interesting problem discussed in Traité élémentaire du calcul des probabilités. Lacroix discusses the "St Petersburg Paradox" first proposed by Nicolaus Bernoulli in 1713.
The problem is as follows: "A fair coin will be tossed until heads appears; if the first head appears on the \n\\th toss, then the payoff is \2n \\ ducats. How much should one pay to play this game?"

TABLE OF CONTENTS OF Traité élémentaire du calcul des probabilités.

OBSERVATION. The greater number of articles indicated in this Table, is composed of those which contain the statements of fundamental propositions or summaries derived from algebraic calculations; the other articles are distinguished by an asterisk.

Preliminary NOTIONS on the meaning of the words CERTAINTY and PROBABILITY,

What mathematical probability is,
Unity, symbol of certainty,
Meaning of the word probable.

SECTION ONE.

Determination of probability, when the number of chances of each kind is assignable, and can be deduced a priori from the statement of the question,

What relative probability is,
What simple probability and composite probability are,
Error that can be made by confusing chances that are not equally possible,

Determination of probabilities in repeated trials of the same chances,

Error of the Chevalier de Méré,

(See the ADDITIONS AND CORRECTIONS placed after the Notes, the kind of paradox advanced by d'Alembert on the difference between the successive throw of a single die and the simultaneous throw of several.)

Composite event most probable in any number of trials,
Probability always increasing in repeated trials, theorem of Jacques Bernoulli.

Consequences of mathematical probability.

Note on the expression degree of certainty,
On the effect of the unequal possibility of chances.

* Questions to serve as examples of a priori determination of probabilities.

* On the use of the development of powers of polynomials, when there are more than two possible events in each test.

On the rule of betting, and of mathematical expectation.

Rule of betting,
Fundamental convention of the game,
Note on the word party,
What mathematical expectation is,
Consequence of inequality in the conditions of the game,
Average value of gains and losses,
Application to the lottery,
What the martingale is.

On moral expectation.

On the moral value of a sum of money,
Rule proposed by Daniel Bernoulli,
* Formula of moral expectation,
* Petersburg problem,
Disadvantages of Daniel Bernoulli's rule, and condition to be fulfilled to determine the fate of the players,
Any calculation would be illusory, without the possibility of repeating the tests.

SECTION TWO

Determination of the a posteriori probability, that is to say, when the total number of chances is unlimited, and its ratios with the number of chances of each kind are unassignable.

Probability of causes, deduced from observed events,
Probability of a new event,
This probability constantly tends to approach the ratios observed in the succession of events,
* Average probabilities,
The probabilities concluded à posteriori can only extend to a number of future events very small compared to that of past events,
On the manner of evaluating the population of a country.

Determination of the probability of causes (or hypotheses) by observations.

The frequency ratio of observed events constantly approaches their true probability, a theorem analogous to that of Jacques Bernoulli,
Application to the births of children of both sexes,
On the connection of effects to causes, and on graduated scepticism,
Continuation of the same subject,
On the philosophical and economic applications of the calculus of probabilities.

Determination of the probabilities of human life.

Formation of mortality tables,
What is probable life,
Mortality curves and Lambert's algebraic formulas, which express its law
Moivre's Hypothesis,
What is the average life,
Its duration and its maximum in various countries,
Distribution of the population according to ages,
* Algebraic theory of population
Probabilities of the duration of the coexistence of several individuals, of marriages and associations,
* On the influence of smallpox on the population,
On the application of the calculus of probabilities to medicine.

On life annuities and insurance on life and on things.

On savings banks,
On insurance on things,
Characteristic effect of insurance.

On the probability of testimonies and decisions.

* On simultaneous testimonies,
On tradition and double erroneous testimony,
* On testimonies concerning extraordinary facts,
General reflections on this subject,
Analogy of decisions rendered by the plurality of voices and testimonies,
The ratio of the number of true judgments to the number of false judgments made by the same voter cannot be assumed to be constant,
Application to some forms of courts,
On elections,
On the middle ground to be taken between several results or observations.

On the moral evaluation of probabilities.

General summary.

1.7.3 Pierre-Simon de Laplace, Essai philosophique sur les probabilités (1814).

The work of the Marquis de Laplace (1749-1827) was enormously influential in the development of mathematical physics, astronomy and statistics. Educated in Normandy, he moved to Paris on obtaining a letter of introduction to d'Alembert, who acted as his mentor while he undertook teaching and independent research in probability, statistics and astronomy. Laplace survived the turmoil of the French Revolution, the rise of Napoleon and the restoration of the Bourbons by a series of manoeuvres which gave him a reputation for insincerity and hypocrisy even among his peers who could correctly assess his contributions to science. His Essai philosophique sur les probabilités, first published in 1814, is a fundamental work which establishes six principles of probability in mathematical terms.

TABLE OF CONTENTS OF Essai philosophique sur les probabilités.

PHILOSOPHICAL ESSAY ON PROBABILITIES

On Probability
General Principles of the Calculation of Probabilities
On expectation
On Analytical Methods of the Calculation of Probabilities.

APPLICATION OF THE CALCULATION OF PROBABILITIES

On Games
On Unknown Inequalities that may exist between chances that are supposed to be equal
On the Laws of Probability, which result from the indefinite multiplication of events
Application of the Calculation of Probabilities, to Natural Philosophy
Application of the Calculation of Probabilities to the Moral Sciences
On the Probability of Testimonies
On the Choices and Decisions of Assemblies
On the Probability of Judgments of Courts
On Mortality Tables and Average Lengths of Life, Marriages, and Any Associations,
On the Profits of Establishments that Depend on the Probability of Events.

On Illusions in the Estimation of Probabilities

On the various causes of illusion.
A great number of these causes are due to the laws of Psychology, or, what amounts to the same thing, of Physiology extended beyond the limits of visible Physiology.
Laws of Psychology.
Principle of sympathy.
Principles of the association of ideas.
Modifications of the sensorium and of the internal impressions of an object, by the often repeated impression of the same object on several senses.
Reciprocal influence of impressions received simultaneously by the same sense, or by different senses, or recalled by memory.
The inclination which leads us to realize the objects of our impressions is due to a particular character which distinguishes these impressions from the products of the imagination and the traces of memory. This inclination deceives in dreams and in visions.
On sleepwalkers and visionaries.
The inclination which leads us to believe in the past existence of objects recalled by memory, is due to a particular character which distinguishes these traces from the products of the imagination.
Effects of memory.
By frequent repetitions, the operations and movements of the sensorium become easy and as if natural.
Effects of this facility on the morals and habits of peoples.
On the transmission of habits, by way of generation.
Influence of attention on the operations of the human understanding.
Explanation of the effects of panoramas.
The repetition of acts similar to those which a particular disposition of the sensorium would produce, can give rise to this disposition.
Influence of this principle on belief.
How one can destroy the illusions which result from it.
The vibrations of the sensorium and the movements which they produce, are subject to the laws of Dynamics.

On the various means of approaching certainty.

Historical notice on the Calculus of Probabilities.

END OF TABLE

1.7.4 Simon Lhuilier, Eléments raisonnés d'algèbre (1804).

This is a two volume work that Lhuilier published in 1804 for his students in Geneva. Speziali writes:

The two-volume 'Éléments raisonnés d'algèbre' that L'Huillier wrote for his Geneva students in 1804 was really a sequel to his texts for Polish schools. The first volume, composed of eight chapters, was concerned solely with first- and second-degree equations. One chapter was devoted to an account of Diophamine analysis. Volume II (chapters 9-22) treated progressions, logarithms, and combinations and went as far as fourth-degree equations. A chapter on continued fractions was based on the works of Lagrange and of Legendre; another concerned the method of indeterminate coefficients. Questions of calculus were discussed in an appendix. The main value of these two volumes lay in the author's clear exposition and judicious selection of exercises, for some of which he furnished solutions.

1.7.5 Leonard Euler, Élémens d'algèbra avec des notes et des additions (1774).

This two volume work is a translation into French of the German edition of Euler's Elements of Algebra. The translation was by Daniel Bernoulli, who was a friend and colleague of Euler. For details of the contents, see 1.5.3 above.

1.8.1 Leibnitii et Johann Bernoulli, Commercium Philosophicum et Mathematica (1740).

This book contains correspondence between Leibniz and Johann Bernoulli. For example, it contains a letter of June 1695 in which Leibniz discusses differentiation with Johann Bernoulli. Here are some other examples. In the second letter in the book, Leibniz writes how delightful the correspondence with Bernoulli becomes for him. In the same letter, he shares his plan for writing De Scientia Infiniti. The tenth letter discusses Powers & Differences, Craig's method of quadrature, the Mechanics of the Construction of Differential Equations, the Mathematical Profession, and several other topics. The 23rd letter discusses the action of gravity, the laws of motion, resistance, and other topics. The 49th letter discusses the curve which cuts straight lines through a given point in such a way that the solid under one segment and the square of the other is given, Tschirnhaus' results, the brachistochrone curve, and other topics.

1.8.2 François Jacquier, Elemens Du Calcul Integral (1768).

This two volume work by Jacquier and Le Seur was written in Parma in 1766-67. They write in the Preface:

... since we already have several Treatises on the Integral Calculus, you are entitled to ask us the reason for our work, and how this work differs from the others that have appeared. Among the different Treatises that we know, some seem to us too elementary, and not very suitable for making known this material; the others are deep and contain the most beautiful discoveries of this kind; but their illustrious authors are great men, who, occupied with the glory of invention, have thought little of the benefits to those who aspire to understand them. It is from these considerations that we attempt, in the Work that we give to the Public, to put our readers within reach of understanding what is most sublime in the Calculus, by requiring no other preparations than those which we have just indicated.

1.8.3 Louis Arbogast, Calcul des derivatives (1800).

In this work operators and functions of operators were separated from the functions on which they act. Arbogast writes in the Preface:

In this work I propose to offer a type of calculation which embraces the theory of sequences, and of which differential calculus is only a particular case: it provides procedures which shorten laborious operations, and formulas which facilitate research in complicated matters; it serves to link together several branches of Analysis: applied to a fairly large variety of objects, it has led me directly, and most often without difficulty, to results, several of which appear new to me, and others presented under a new aspect. This method of calculation is based on a general way of considering quantities as deriving from one another; this is what made me name it Calculus of Derivations.

To get an idea of ​​derivations, we will observe that quantities or functions which we deduce from each other by a uniform process of operations, are derived quantities; such are the successive differentials. We can extend this idea by considering quantities which derive from each other, not in themselves, but only in the operations which assemble them and link them together; the quantities themselves being arbitrary, independent. Thus, by supposing that of several different letters the first enters alone into a function, while the first two enter into the derivative of this function, that the first three enter by the same law into the derivative of this derivative, and so on; we will have derivatives in the extended sense which I have given them. Here the quantities designated by the different letters do not derive from each other; and the derivatives that I consider are less derivatives of quantities than derivatives of operations, just as Algebra is less a calculation of quantities than of arithmetic or geometric operations to be performed on quantities.
...
This method is generally thought of as separating from the functions of variables when possible, the operational signs which affect this function. Then, of treating the expression formed by these signs applied to any quantity whatsoever, an expression which I have called a scale of operation, to treat it, I say, nevertheless as if the operational signs which compose it were quantities, then to multiply the result by the function.

1.9.1 Isaac Newton, Philosophiae Naturalis Principia Mathematica (1739-42).

This is the Jesuit Edition of Newton's Principia which is annotated and appears in four volumes rather that Newton's original three volumes. Edited by Thomas Le Seur and François Jacquier, it acknowledges the contributions of Jean-Louis Calandrini in the Preface to the first volume:

We do not wish to omit public evidence of our gratitude towards the illustrious Calandrini, Professor in the Academy of Geneva, very proficient in matters mathematical, who arranged that our edition of Newton's 'Principia', enriched by many additions, would be readied to the elegant standard of the edition that appeared in London in the year 1726. Furthermore, that very learned man took upon himself the labour not only of checking carefully that the figures be engraved, and placed in the appropriate places, and that the typographical errors be corrected, but also of writing those elements of conic sections that we have already praised, and those things that appeared as not treated clearly enough by us, he occasionally elucidated with his own notes.

1.9.2 Luigi Rasori, Trigonometria Piana (1842).

This book, published in Bologna, has the subtitle, "Elementary treatise on plane trigonometry preceded by the geometric construction of equations of the 1st and 2nd degree with at the end the Tables of logarithms of natural numbers from 1 to 101000 and of sines, cosines, tangents and cotangents from minute to minute with the first 4 degrees of 10 in 10 seconds." Rasori directed a school in elementary philosophy under the auspices of Archbishop Carlo Oppizzoni, Archchancellor of the Pontifical University of Bologna.

Carlo Renaldini, Ars Analytica Mathematum (in three parts) (1665).

In this work Renaldini covered algebra, geometry, and basic mathematics principles studied with a philosophical approach. Much of Renaldini's career was spent as philosopher so his mathematics was naturally influenced by his philosophical approach.

Rene Descartes's Compendium musicae was one of the most widely-read Latin texts on the mathematics of music in the second half of the seventeenth century, offering a succinct and lucid summary of its subject. It was first published in 1653 but copies of this first edition do not seem to have survived. This is the 4th edition with woodcut illustrations published in Amsterdam by Typographica Blaviana in 1683.

Pietro Mengoli published Speculationi di musicae in Bologna in 1670. The book is written in Italian. On the title page he records that he is Dottor dell'una, e l'altra Legge, e di Filosofia Collegiato, Prior di S Maddalena, e Publico Professor di Scienze Mecaniche nello Studio di Bologna. This highly original work attempted to create a mathematical study of music based on the anatomy of the ear. In the book he criticised the theory of resonance which had earlier been formulated by Galileo. Benjamin Wardhaugh gives the following summary in his 2007 Annals of Science paper The Logarithmic Ear: Pietro Mengoli's Mathematics of Music:

In 1670, the Bolognese mathematician Pietro Mengoli published his 'Speculationi di musica', a highly original work attempting to found the mathematical study of music on the anatomy of the ear. His anatomy was idiosyncratic and his mathematics extraordinarily complex, and he proposed a unique double mechanism of hearing. He analysed in detail the supposed behaviour of the subtle part of the air inside the ear, and the patterns of strokes made on the eardrum by simultaneous sounds. Most strikingly, he divided the musical octave into a continuous set of regions which he colour-coded to show their effects on a listener. His work did not find its way into the mainstream of seventeenth-century mathematical studies of music, but when examined in its context it has the potential to shed light on that discipline, as well as being of considerable interest in its own right. Here, I focus on the anatomical and mathematical basis of Mengoli's work.

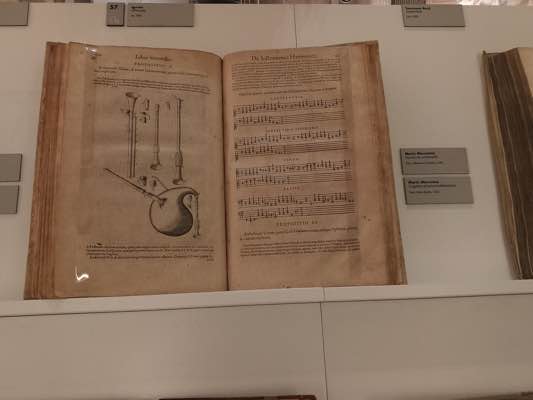
Marin Mersenne published Harmonie universelle in Paris in 1636. It was a comprehensive study of the theory of music describing in detail all that was known about music in France at the time of writing. On its title page it lists the topics covered: the nature of sounds; movements; consonance; dissonance; genres; modes of composition; voice; singing; and the full range of harmonic instruments. Notice Mersenne's mathematical style of presenting material with Propositions. There are at least two copies of the 1636 edition on view in the Museum.

Leendert van der Miesen wrote the paper 'Unbelievably hard work': Marin Mersenne's Harmonie universelle at the printers published as Chapter 10 of the 2021 Routledge book Early Printed Music and Material Culture in Central and Western Europe. Here is the Introduction to that paper:

The French scholar Marin Mersenne (1588-1648) described the process of getting his 'Harmonie universelle' printed as 'unbelievably hard work'. He finished the manuscript in 1634 after ten years' work, but could only send the complete printed work to his friend and patron Nicolas-Claude Fabri de Peiresc in 1637. During the three years of printing, the voluminous book was produced piecemeal. According to Mersenne, the primary cause of the delay was the intervention of Pierre Ballard, the Music Printer to the King. Ballard famously held the privilege on music printing in France, and with this privilege, Ballard was the only one who could print musical notation or allow others to do so. Mersenne's dissatisfaction with Ballard has long been noted, and traces of the chaos attending the printing process can be found throughout the work. However, little attention has been given to the role of music printing in Mersenne's work. The technique of music printing, the presses of Pierre Ballard and the royal privilege are important elements in understanding how we encounter the 'Harmonie universelle' today. Moreover, Mersenne's role as an author and intermediary in early modern print culture still demand closer investigation. This chapter attempts to locate Mersenne at the printing press, to see how he negotiated, brokered and handled the restrictions and possibilities of music printing in early seventeenth-century Paris.

Readers of the 'Harmonie universelle' have long commented upon its complex structure. The number of books is said to differ with each copy. This is complicated by the fact that there are three variants, each with a different printer on the title page. The majority of the surviving copies were published under the names of Sébastien Cramoisy and Pierre Ballard. The second variant features only Ballard's name on the title page. The third variant is published under the name of Richard Charlemagne. Mersenne's own copy - the one by Cramoisy and Ballard - is full of improvements and alterations, indicating that the result continued to bother him. Simultaneously, Mersenne published the Latin counterpart of his book, the 'Harmonicorum libri', made for those who could not read French. It was printed by Guillaume Baudry with Ballard's musical characters in 1635 and reissued the next year with a new preface of the printer. The Harmonie contains newer material that was only added after 1636. Nonetheless, the Latin version also contains material that cannot be found in the French book, thus confusing its history even more.

Marin Mersenne published the three volume work Cogitata physico-mathematica in Paris in 1644. He writes on the title page, "In quibus tam naturae quàm artis effectus admirandi certissimis demostrationibus explicantur" [In which the most admirable effects of nature as well as of art are explained by the most certain demonstrations]. In this book Mersenne gives details of the work of other scientists and also details of his own research findings. The topics covered include metrology, hydraulics and pneumatics, hydrostatics, acoustics and musicology, mechanics, and ballistics. His own investigations include work on prime numbers, acoustics, harmony, tunings and music theory. The third volume begins with an examination of the heliocentric theory of Aristarchus. This is followed by an examination of the physics of Galileo and a series of Galilean experiments on gravity, acceleration, percussion, and hydraulics, along with the Torricellian experiments with the mercury barometer.

The book Rudimenta Musices was published 1557 and attributed to Euclid. It is, however, now accepted that the Introduction to Harmonics is the work of Cleonides and was probably written in the 2nd century AD. There is no agreement, however, who is the author of another part of the work:

Greek text and Latin translation of the "Introduction to Harmonics" by the Greek scholar Cleonides, the pupil of Aristoxenus, erroneously ascribed to Euclid, and of the "Division of the Scale", about whose true authorship there is no agreement. Edited by the French mathematician and educator Péna (ca. 1528-68), the book reflects the influence of classical mathematicians on Renaissance music theory and was a key work for the wide distribution of music theory of the classical period. The attribution of the "Eisagoge" to Euclid (or to Pappus in some manuscripts) is incompatible with the Aristoxenian approach adopted in the treatise, namely that "the scale is formed of notes separated by a tone identified by the ear". Cleonides's treatise is the clearest account of the technical aspects in the work of the philosopher Aristoxenus, who defined key terms of music theory, including the interval, whole tone and semitone, pitch space, and rhythm. The other musical work here ascribed to Euclid, the "Sectio canonis", expounds a quite contrary theory, namely "the Pythagorean doctrine that the musical intervals are to be distinguished by the mathematical ration of the notes terminating the interval. All that it seems possible to say with certainty is that Euclid wrote a book entitled 'Elements of Music' and that the 'Sectio canonis' has some connection with it.