Casey's theorem

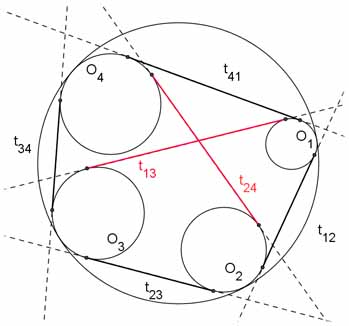
Let $O$ be a circle. Let $O_{1}, O_{2}, O_{3}, O_{4}$ be (in that order) four non-intersecting circles that lie inside $O$ and tangent to it. Denote by $t_{ij}$ the length of the exterior common bitangent of the circles $O_{i}, O_{j}$.
Then: $t_{12} . t_{34} + t_{23} . t_{41} = t_{13} . t_{24}$.

In the degenerate case, where all four circles reduce to points, this is Ptolemy's theorem.