Catalan numbers
The Catalan numbers: 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, ..., named after Eugéne Charles Catalan (1814--1894), arise in a number of problems in combinatorics.
They can be computed using the formula:
and satisfy the recurrence relation ,
Among other things, the Catalan numbers describe
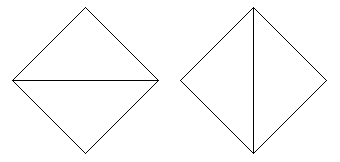
5 sides, 5 ways:

6 sides, 14 ways:
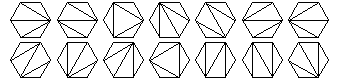
7 sides, 42 ways:
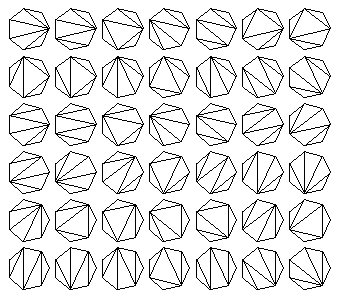
8 sides, 132 ways:

9 sides, 429 ways:

3 numbers:
4 numbers:
5 numbers:
6 numbers:
3 nodes:
4 nodes:

5 nodes:

6 nodes:
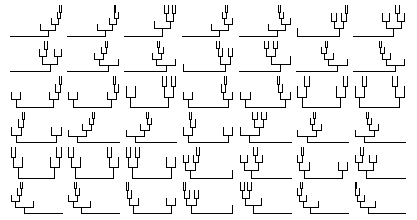
7 nodes:
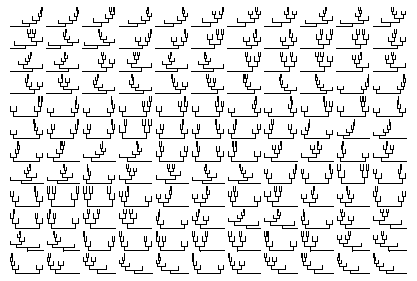
8 nodes:

= 2

= 3

= 4

= 5
Robert M Dickau, Heinz Klaus Strick
They can be computed using the formula:
and satisfy the recurrence relation ,
Among other things, the Catalan numbers describe
- Polygons: the number of ways a polygon with sides can be cut into triangles.
- Parentheses: the number of ways in which parentheses can be placed in a sequence of numbers to be multiplied, two at a time.
- Trees: the number of rooted, trivalent trees with nodes.
- Paths: the number of paths of length through an grid that do not rise above the main diagonal,
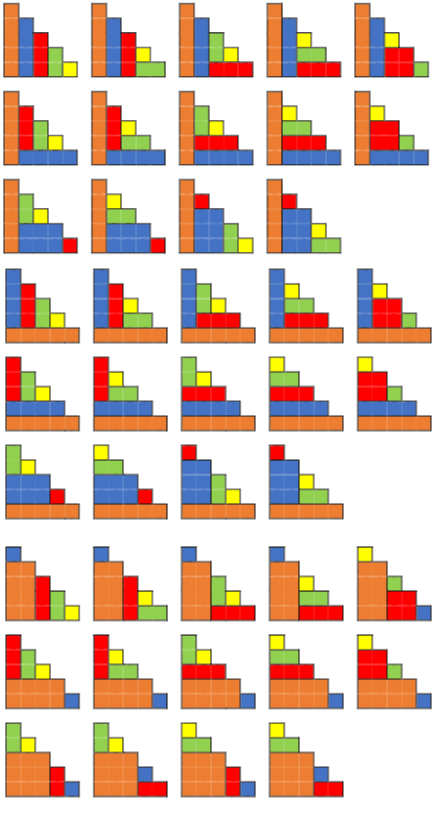
- Stairs: the number of ways to decompose a staircase-shaped figure with steps into rectangles.
Polygons
4 sides, 2 ways:
5 sides, 5 ways:

6 sides, 14 ways:

7 sides, 42 ways:
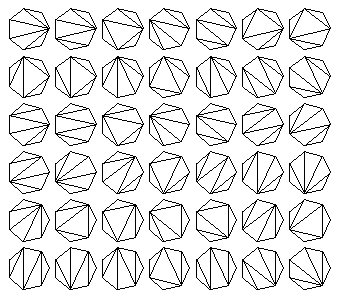
8 sides, 132 ways:

9 sides, 429 ways:

Multiplication diagrams
3 numbers:
(1 (2 3)) ((1 2) 3)
4 numbers:
(1 (2 (3 4))) (1 ((2 3) 4)) ((1 2) (3 4)) ((1 (2 3)) 4) (((1 2) 3) 4)
5 numbers:
(1 (2 (3 (4 5)))) (1 (2 ((3 4) 5))) (1 ((2 3) (4 5))) (1 ((2 (3 4)) 5)) (1 (((2 3) 4) 5)) ((1 2) (3 (4 5))) ((1 2) ((3 4) 5)) ((1 (2 3)) (4 5)) ((1 (2 (3 4))) 5) ((1 ((2 3) 4)) 5) (((1 2) 3) (4 5)) (((1 2) (3 4)) 5) (((1 (2 3)) 4) 5) ((((1 2) 3) 4) 5)
6 numbers:
(1 (2 (3 (4 (5 6))))) (1 (2 (3 ((4 5) 6)))) (1 (2 ((3 4) (5 6)))) (1 (2 ((3 (4 5)) 6))) (1 (2 (((3 4) 5) 6))) (1 ((2 3) (4 (5 6)))) (1 ((2 3) ((4 5) 6))) (1 ((2 (3 4)) (5 6))) (1 ((2 (3 (4 5))) 6)) (1 ((2 ((3 4) 5)) 6)) (1 (((2 3) 4) (5 6))) (1 (((2 3) (4 5)) 6)) (1 (((2 (3 4)) 5) 6)) (1 ((((2 3) 4) 5) 6)) ((1 2) (3 (4 (5 6)))) ((1 2) (3 ((4 5) 6))) ((1 2) ((3 4) (5 6))) ((1 2) ((3 (4 5)) 6)) ((1 2) (((3 4) 5) 6)) ((1 (2 3)) (4 (5 6))) ((1 (2 3)) ((4 5) 6)) ((1 (2 (3 4))) (5 6)) ((1 (2 (3 (4 5)))) 6) ((1 (2 ((3 4) 5))) 6) ((1 ((2 3) 4)) (5 6)) ((1 ((2 3) (4 5))) 6) ((1 ((2 (3 4)) 5)) 6) ((1 (((2 3) 4) 5)) 6) (((1 2) 3) (4 (5 6))) (((1 2) 3) ((4 5) 6)) (((1 2) (3 4)) (5 6)) (((1 2) (3 (4 5))) 6) (((1 2) ((3 4) 5)) 6) (((1 (2 3)) 4) (5 6)) (((1 (2 3)) (4 5)) 6) (((1 (2 (3 4))) 5) 6) (((1 ((2 3) 4)) 5) 6) ((((1 2) 3) 4) (5 6)) ((((1 2) 3) (4 5)) 6) ((((1 2) (3 4)) 5) 6) ((((1 (2 3)) 4) 5) 6) (((((1 2) 3) 4) 5) 6)
Tree diagrams:
3 nodes:

4 nodes:

5 nodes:

6 nodes:

7 nodes:
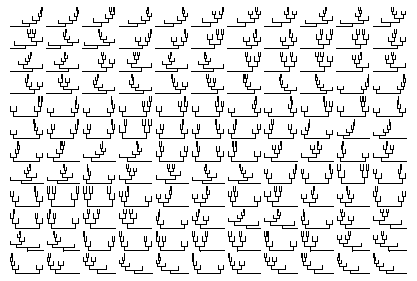
8 nodes:

Path diagrams:
2 x 2 grid:
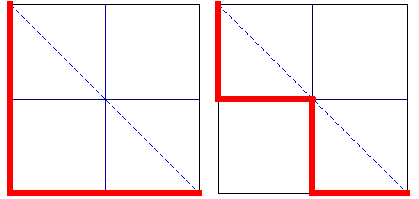
3 x 3 grid:

4 x 4 grid:
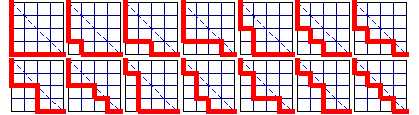
5 x 5 grid:

6 x 6 grid:

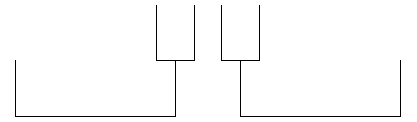
Staircases:
= 2

= 3

= 4

= 5

Robert M Dickau, Heinz Klaus Strick
References (show)
- B Hayes, A Question of Numbers, American Scientist, January-February 1996
- S S Skiena, Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, Addison-Wesley, 1990
- F S Roberts, Applied Combinatorics, Prentice-Hall, 1984
- D E Knuth, Sorting and Searching (vol. 3 of The Art of Computer Programming), Addison-Wesley,
- Martin Gardner, Time Travel and Other Mathematical Bewilderments, chapter 20, W. H. Freeman, 1988.
- Ilan Vardi, Computational Recreations in Mathematica, chapter 9, Addison-Wesley, 1991.