Catalan solids

A Catalan solid is the dual of an Archimedean solid.

The non-regular faces of these Catalan solids are all congruent to each other. At the vertices, however, different numbers of faces meet. In the case of the Archimedean solids, it is the other way round: the number of faces coming together at a vertex is always the same, but the faces are different types of regular polygons.

In the list below the number of faces, edges and vertices are listed as (F, E, V).

Picture	Name	F, E, V
	Triakis tetrahedron dual of the Truncated tetrahedron	12, 18, 8
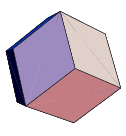	Rhombic dodecahedron dual of the Cuboctahedron	12, 24, 14
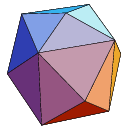	Tetrakis hexahedron dual of the Truncated octahedron	24, 36, 14
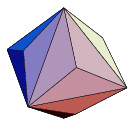	Triakis octahedron dual of the Truncated cube	24, 36, 14
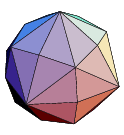	Deltoidal icositetrahedron dual of the Rhombicuboctahedron	24, 48, 26
	Disdyakis dodecahedron dual of the Truncated cuboctahedron	48, 72, 26
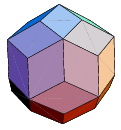	Rhombic triacontahedron dual of the Icosidodecahedron	30, 60, 32
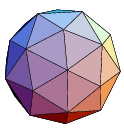	Pentakis dodecahedron dual of the Truncated icosahedron	60, 90, 32
	Triakis icosahedron dual of the Truncated dodecahedron	32, 90, 60
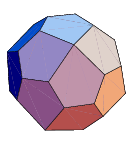	Pentagonal icositetrahedron dual of the Snub cube	24, 60, 38
	Deltoidal hexecontahedron dual of the Rhombicosidodecahedron	60, 120, 62
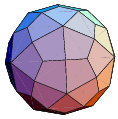	Dadakis triacontahedron dual of the Truncated icosidodecahedron	120, 180, 62
	Pentagonal hexecontahedron dual of the Snub dodecahedron	24, 150, 92

Pictures are from https://mathworld.wolfram.com