Finlay Freundlich's Inaugural Address, Part 2
On 29th January 1952 Professor E Finlay Freundlich, Dr. Phil., M.A., Napier Professor of Astronomy in the University of St Andrews delivered his Inaugural Address. Below is the second part of the address.
The first part is here: Freundlich's Inaugural, Part 1
The first part is here: Freundlich's Inaugural, Part 1
The Educational Value of the Study of Astronomy
(3) This is most decidedly so too in the last case which I wish to discuss. It concerns a problem which formerly was thought to be the domain of pure mathematics - I am thinking of geometry. Until only about 40 years ago it was believed that the laws according to which distances in space are measured were given by Euclid's laws of geometry, the first mathematical system systematically and consistently built up from axioms, i.e. assumptions thought to be logically indisputable. However, full agreement whether Euclid's fundamental axioms were really all indisputable, that means whether the omission of one of them would necessarily lead to an inconsistency in the resulting Geometry, was never reached. About one century ago, however, three mathematicians (Gauss, Bolyai and Lobachevsky) nearly simultaneously came to the conviction that one of the axioms in Euclid's theory could be dropped, i.e. lacked the a priori certainty necessary for an axiom. This opened the way to new geometries - they were called non-Euclidean geometries - based on axioms differing from Euclid's. In the beginning these new geometries were thought to be of purely mathematical interest. It was still taken for granted that the laws, according to which distances in physical space have to be measured, remained those given by Euclid's geometry.
It is, however, usually not realized, that when proving the congruency of triangles in geometry very definite assumptions as to the free mobility of rigid bodies in space have to be made. For instance when it is proved that two triangles are congruent, which have in common two sides and the angle formed by these two sides, say , and the angle at equal to the angle at , there are two possible ways of drawing such couples of triangles as shown in the sketch.
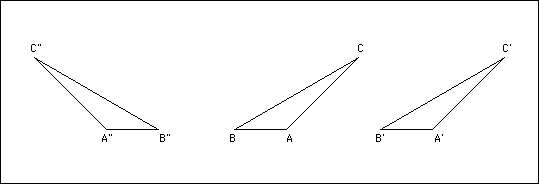
To prove in the first case that is congruent to , one imagines the triangle moved until falls upon ; then it is turned until the line falls in line with ; since the length equals , will fall upon ; and since the angle at equals that at , also the side will fall in line with and will fall upon , so that obviously the two triangles can be brought to cover each other completely.
In the second case, however, which differs from the first only by the instance that the corresponding sides in the two triangles follow each other clockwise, while in the triangles and it is counter-clockwise, the process of bringing the two triangles to cover each other necessitates that one of them has to be turned over, so that the back of comes to lie on . If the triangles are drawn in a plane and are considered to be freely movable, not only in the plane but also in space, this does not introduce any additional difficulty. But let us make the assumption that the two triangles are drawn on the surface of a sphere, so that the surface of each triangle is curved. Then the first proof concerning and will still remain valid; but in the second case, when the one triangle has to be turned over, the curvature of their surfaces will prohibit them from covering each other, and the proof cannot be accomplished. And much more complex the laws become if the triangles were drawn on the surface, say, of an egg, on which the curvature changes from place to place. Therefore, when investigating the metric laws of triangles on a not necessarily plane surface, respectively in general of rigid bodies in a possibly curved space, certain demands concerning the free mobility of rigid bodies in space have to be satisfied.
In fact the laws of Geometry of triangles drawn on the surface of a sphere differ systematically from the laws of Euclid's Geometry in the plane. The spherical geometry is the most simple case of a non-Euclidean geometry. It has to be applied to all astronomical observations which concern relative positions of stars as they appear to the observer fixed to the celestial sphere. When, however, the true distances of celestial bodies in space are considered, it was still taken for granted that the laws of Euclidean geometry have to be applied. But shortly after, on purely mathematical grounds, the knowledge of consistent non-Euclidean geometries had been conceived, i.e. geometries which give metric laws for spaces of positive or negative curvature, it was the mathematician Riemann, who, in 1854, for the first time clearly stated that in physical space, that means in the space in which all phenomena of natural science proceed, the laws of geometry must be determined by the forces which act between the celestial bodies. The geometry of physical space is not given a priori. The Euclidean geometry would be strictly applicable only if no forces were acting and if rigid bodies were absolutely freely movable in space. That this assumption is of really general and fundamental importance has been investigated and discussed with all rigour, when the foundations of geometry were in the forefront of discussion during the last century.
Now it is exactly the main experience, which is laid down in the laws of gravitation, that we never experience that a body is freely movable in space. Every body on the Earth is forced by gravitation to fall towards the Earth's centre. The Moon, unable to move straight on in the direction it is taking at any moment, is forced to follow the orbit prescribed by the gravitation of the Earth. Earth and Moon together are similarly enchained by the gravitation of the Sun, and so on. It is on principle impossible to visualise any really freely mobile body anywhere in the space of the Universe. The existence of even two bodies only in the Universe would mean that they have lost their free mobility due to their mutual attraction.
This gravitational force which deprives all bodies of their freedom of motion is, moreover, in contradistinction to all other known physical forces, like electric or magnetic forces, of absolutely universal character. While bodies are easily found which are not attracted or repulsed by a magnetic pole, respectively by an electrically charged body, gravitation is inherent in matter as such. It does not manifest any specific behaviour, depending for instance on the chemical constitution of the attracting body, etc. Alone, the mass, measured on the Earth by the weight, in celestial space by the properties of orbital motion, determines the degree by which the free mobility of another body is impeded.
So it is not surprising that, in accordance with Riemann's prediction (that some physical force must be responsible for the geometric conditions in physical space) gravitation was singled out as the force playing this fundamental roll.
This is the crucial assumption on which Einstein's general theory of relativity is based. The theory of relativity teaches us that the Earth, placed at a certain distance from the Sun and given an initial speed, will be guided, due to the Sun's gravitation - as if an invisible surface connected the two subsequent orbital positions - along the shortest path which connects these two positions. But due to the changed geometrical conditions of space, arising from the gravitational field produced by the Sun, this shortest connection is no longer a straight line of Euclid's geometry, but the arc of a Kepler orbit. It is no longer appropriate to talk of a force exerted by the Sun upon the Earth, as Newton's law implies; for, as there is no bodily connection between Sun and the planets, or between the Earth and the Moon, it is impossible to envisage how a gravitational attraction should act. In the theory of relativity no such force is envisaged. The existence of gravitation manifests itself in changed laws of geometry. The geometry of physical space is not given a priori, but depends on the distribution of masses in space. The changed geometry determines the mobility of the bodies in space and thus the orbits along which they have to move.
It is perhaps one of the most astounding discoveries, that a theory of motion, based on these new ideas, which do not seem to have any relationship whatsoever with the ideas on which Newton's theory was based, should lead to practically the same laws of motion for two gravitating bodies; namely, the laws which Kepler embodied in his three laws of planetary motion. And, what is of even greater importance, the coincidence between the Kepler orbit and the orbit of a planet moving according to the theory of relativity in a quasi non-Euclidean space, is not complete. A small difference remains between the old and the new theory. This difference corresponds accurately, in value and character, to the deviation in the motion of Mercury, which had been discovered long before the theory of relativity was conceived and which I have already mentioned. It is a slow rotation of the axis of Mercury's orbit, by 43" of arc in a century. This rotation, disclosed by astronomical observations long ago, cannot be explained on the basis of Newton's theory of gravitation.
Again we experience that it is astronomical research that made it possible to investigate this profound problem concerning the foundations of the geometry in physical space. This problem has by no means been solved satisfactorily yet. For a full agreement between the predictions of the theory of relativity and astronomical observations has not yet been achieved in all observable effects. While the motion of a body, like Mercury, seems to follow the laws set up by the theory of relativity, light, i.e. energy, propagated through space seems to follow a different law. Here astronomy is presented with a new problem, which may be of decisive influence upon the whole future development of physics.
The theory of relativity teaches that between matter and energy no fundamental difference exists in so far as the one may be converted into the other. Matter and energy may be understood to be only different forms of appearances, of energy, if this is considered to be the basic reality, of matter, if matter is considered to be the more fundamental reality.
The theory of relativity claims therefore that the same laws of motion hold good for moving energy as for moving matter. When a ray of light passes near to the Sun, the gravitational field of the Sun must affect the propagation of the light. The ray will describe an orbit, similar to the orbit of a moving planet. This assumption leads to an observable effect; it is a measurable deflection of the light of a star passing near to the Sun. This deflection depends on the solar mass and on the distance at which the light beam passes the Sun, and is large enough to be accurately measured. But the observations yield a considerably larger value for the deflection than is predicted by the theory of relativity. The difficulty of safely establishing this difference lies chiefly in the circumstances under which the experiment has to be made, namely, during the few and exciting minutes of a total eclipse. This makes it extremely difficult to derive this deflection with the very great accuracy which the importance of this effect demands. Preparations to make the necessary observations during future eclipses are already under way. Should the results yield again a value for the light deflection considerably larger than the theoretical prediction, it would mean that the laws of motion for energy differ systematically from those for moving matter. Although followers of Einstein's theory of relativity are reluctant, to say the least, even to consider such a possibility, it may not be overlooked that also in other respects a deep gap is dividing the two branches of physics the one approaching the phenomena from a macroscopic point of view; this is the theory of relativity; the other, the quantum theory, based on fundamentally different conceptions, which takes account of the atomic structure of matter and the quantum structure of energy.
These two branches are not yet linked together to one unified and consistent picture of the Universe. Should the astronomical observations give finally a different value for the light deflection, as predicted, this fact may open a way to bridge the gap between the macroscopic and microscopic pattern of Nature. Here again, astronomy holds the key position to a final solution.
I have deliberately discussed today only problems in which Astronomy appears intimately interlinked with neighbouring branches of science, with problems that concern the foundations of pure science, problems which arouse the interest of a much wider circle than those who study astronomy. Astronomy is not only the pleasure-ground for star-gazers; the work of the Astronomer is not so secluded from the world as people usually believe. It is true, the routine work does not bring an Astronomer continuously face to face with these fundamentals of natural science. But even if his work does not normally have any immediate connection with these problems, somehow all astronomical research contributes to the final picture of the Universe.
The three problems which I discussed are of such a depth and of such a generality that their educational value is beyond any doubt. They touch the most fundamental questions of Physics, Chemistry and Mathematics; Unless we deny that knowledge, that a rational understanding of the Universe as such raises the cultural level of man, the advancement of human culture by the advancement of astronomical knowledge can hardly be overestimated.
The value of science has been too frequently measured with the yardstick of successful exploitation of the riches of nature for the benefit of man. That is not the stimulus which incites men to devote their lives to science. The right attitude in this respect was pronounced by Kepler 350 years ago; let me cite therefore a passage from Kepler's Mysterium Cosmographicum, from 1596:-
Who has no longing for these things resembles more a dead than a living man: As nature provides the living world with food, we may state with equal right, that Nature has been so richly endowed that the human spirit may never lack fresh nourishment, never get tired of the old, nor find peace; but always find this world an open workshop for the development of his mind.But his mind must be open and willing to develop beyond the frame, which traditional knowledge and creeds tend to fix.
For the propagation of knowledge, which removed the Earth, and thus also Man, from the centre of the Universe, men have fought and have risked their lives. The development of Astronomy in all its outlooks during the last decades has affected man's place in the Universe in an incomparably deeper and more revolutionary way than the transition from the antique view to the Copernican picture of the World. But modern man apparently does not take these questions any longer so seriously; not because he is more enlightened than our ancestors were 300 years ago, but because we have become materialistic and self-confident. Our minds are no longer orientated outwards towards the cosmos, but horizontally, i.e. parallel to the surface of the earth, from which we try to derive the maximum of riches to embellish our lives. In consequence we have not yet realized which educational values can be gained from the right approach to Nature, from the rich pattern of the laws that rule all phenomena and from a deep devotion to the mystery of the Universe which Astronomy is able to fathom to nearly infinite depths.
Last Updated April 2007