MacTutor logo MacTutor

Henryk Iwaniec delivered the Casimir Funk Award lecture "Mathematical concepts, some research questions and a bit of history" on 12 May 2021. It was presented as part of the Kosciuszko Foundation Collegium of Eminent Scientists Lecture Series and was combined with the presentation of the Casimir Funk Natural Sciences Award to Professor Iwaniec by the President of the Polish Institute of Arts and Sciences, Professor Robert Blobaum. The lecture attempted to present Henryk Iwaniec's view of mathematics to a general audience. Being an award for scientists with a Polish background, he naturally emphasises Polish mathematics and mathematicians.

Mathematical concepts, some research questions and a bit of history, by Henryk Iwaniec.

I don't know what to say. Let me say just briefly that I'm delighted to receive the Casimir Funk Award and to join this group of distinguished recipients. It is particularly precious for me because it refers to my Polish origin and Polish heritage. I thank the committee of the Polish Institute of Arts and Sciences of America for just, you know, finding me in the crowd of very remarkable scholars in the United States of America with Polish connections. I also would like to thank the Kosciuszko Foundation for having me today to speak about mathematics, my beloved subject, my life. So thank you very much for having me and for all these awards and let me go to the business.

So let me talk about mathematics. What is mathematics? For many of the people, we know it brings some scary memory from school. Particularly among students the fear of mathematics is just unbelievable. There are reasons for it. Maybe one is that mathematics is a pretty abstract subject. No shape like physics, biology, chemistry, medicine etc. It's really abstract but maybe another reason is very bad teaching. Let me say something about my own experience. I remember going back home and the immigration officer was curious to know what I'm doing for a living in the United States. So I said that I do mathematics, research and teaching. He immediately responded, I would say with some pride, proudly, that he was very bad in mathematics. This is a typical reaction even among educated people, I mean prejudice to mathematics. I think it's unfair and it shouldn't be there, you know, because once you've learned concepts of mathematics and its beauty and nice aesthetic effects you really must like it. There's no way back once you learn this and mathematics is like life, like love, you know it's pretty personal and intimate. It can be complicated nevertheless, so let me just tell you a short story about teaching in mathematics.

1. Introduction.
Reality is an illusion of the mind.
Platonic reality is a different kind than physical reality.
Truths of mathematics are absolute!
Plato (~400 BC)

A famous mathematician named Gelfand, Israel Gelfand, who is very well recognised for his contribution to pure mathematics, was a giant of 20th century. He was also recognised for his passion for education on all possible levels, elementary, high school and college education. So immediately when he immigrated to the United States he was asked by a reporter from some public newspaper to explain why it is so that people don't like mathematics. I mean what's wrong with the teaching of mathematics? He said, "well it's a matter of approach. One can clear your point please. So okay let's for example do this. Ask a pedestrian on a Moscow street which number is larger two-thirds or three-fifths. Many people would have had time to figure it out but you may ask the same question slightly differently. Ask what do you prefer, what would you choose, two bottles of vodka for three people or three bottles of vodka for five people. I bet no problem of finding the correct number." So this is a joke that I know directly from Israel Gelfand. He was actually, you know, having his office in Rutgers University next to mine so I had a lot of contact with him. He was a very nice person but that's not the subject of my of my lecture here so let's try to be a little bit serious.

I think the popular perception of mathematics is that it's just counting, right. Counting objects, time, volumes, measuring things, counting. That's the early occupation of people with mathematics and already then, long long ago, people who started thinking abstractly they associated symbols with numbers. In this context, you know, finger counting was just adding fingers etc. But people started really thinking abstractly so they just started using operations on numbers, adding, subtracting, and dividing. Sometimes they got negative numbers sometimes they got zero. Well that was a problem for quite a while to understand the concept of zero. I mean the cardinality of nothing, it was really a philosophical problem that's long long ago. I think everybody today comprehends what this number zero stands for and this famous quotation of Kronecker was already said ...
God made the integers; all else is the work of man.
Leopold Kronecker (1823-1891)
... so I won't repeat it.

But this is lovely, it is related to what I'm saying in the moment about modern models of mathematics. We start from something very fundamental without any questions, like the integers. Kronecker said that "God made the integers all else is the work of man" - yes and no. Let's see how we explain that. So integers, whole numbers, were not sufficient for expressing things in life. You know they're not. People introduced fractions, rational numbers, and that was a pretty large set but still both integers and rational numbers are countable so you know in a sense they are not much larger, the set of rational numbers versus integers. But then people, even though you can approximate many things with rational numbers, they were not good enough for questions in science. Sometimes you need really exact answers, so people introduced real numbers, these numbers are limits of sequences of rational numbers like the square root of two, for example, or π.

2. Arithmetic and number theory

1, 2, 3, 4, 5, 6, 7, 8, 9, 20, ... integers

12,13,14,35,26,...\large\frac{1}{2}\normalsize , \large\frac{1}{3}\normalsize , \large\frac{1}{4}\normalsize , \large\frac{3}{5}\normalsize , \large\frac{2}{6}\normalsize , ... rational numbers

√2 = 1.4142..., π = 3.1415..., real numbers

1+i√2,2πi,a+bi,...1 + i√2, 2\pi i, a + bi, ..., complex numbers

a+bi+cj+dk,...a + bi + cj + dk, ... , Hamiltonian quaternions (1843);

You see some algebraic numbers are transcendental numbers. By the way I'll be using certain terminology of mathematics and I know - I'm fully aware - that many of you here listening, you don't know that terminology. But I hope that at least you get some impression what it is. Never mind definitions. Okay so real numbers were introduced, interesting enough, pretty late in the 19th century. It was pretty late, I mean, with the correct precise rigorous definition of real numbers. Real numbers were already in operation by human beings long long ago but the definition with precise mathematical rigour was only made in the 19th century by Cauchy and Dedekind. Well not everything would be possible to study with tools using real numbers. People, for analysis particularly, extended further. The real numbers, by the way, is a much larger set than the rational numbers or integers. I'll come to this issue a bit later. The continuum, it's a much bigger set even though both are infinite sets. You know that there is a distinction of cardinalities in some sense. So the real numbers are still not sufficient, so people started adding something extra like imaginary numbers with i, which is a square root of minus 1, and put numbers in coordinates with complex numbers and these were really a complete set sufficient for doing modern analysis. Complex numbers are really the ultimate object of current analysis so to speak. Sometimes operations with numbers were not commutative and that means operations depends on the order of execution, that aa times bb is not necessarily bb times aa in certain systems. For example Hamiltonian quaternions, which are four-dimensional, are an example of this. Knowledge of current science really requires non-commutative systems, particularly in n dimension, many dimensions, like representation theory. So it's not just something that people invent, it's really something that is needed, very much needed, but I will not talk about it.

Arithmetic is one of the first theories of mathematics. It deals with number theory which is an extension of arithmetic by tools, a much larger collection of tools, particular analysis. That's what number theory is versus arithmetic but the fundamental result of the theorem of arithmetic tells you that every positive integer is a product of prime powers which is unique as a product. That's Euclid in 300 BC, more or less, who first systematised knowledge of mathematics that possesses all geometry but let me continue about arithmetic. So prime numbers were already in focus. What are these prime numbers? Just numbers which are only divisible by themselves and by one, no other divisors. So it's like elementary particles in the theory of matter, like in physics, the arithmetic is built out of prime numbers and Euclid was first - I'm not sure if he was first - but he produced a proof that there are infinitely many prime numbers. This is a wonderful moment for mathematics because it introduced the idea of proving by contradiction.

There are infinitely many prime numbers :
2, 3, 5, 7, 11, 13, 17, 19, ...
The largest known prime is the 51st Mersenne prime:
282,589,933−12^{82,589,933} - 1, having 24,862,048 digits, found by Patrick Laroche in 2018.
[Actually, the largest known prime is now 2136,279,841−12^{136,279,841} - 1 with 41,024,320 digits found by Luke Durant in 2024]

So there are infinitely many primes but still people like to have the largest known prime, the largest that you can write down or memorise, so here is the one that I figured out from the internet. This was found three years ago, it is a number which has 25 million digits. I don't think you can memorise all these digits but I challenge you to memorise all the digits in binary system of that number. It's a joke, please try it.

All right, but seriously enough the distribution of prime numbers is the fundamental matter in number theory and a bit also in mathematics I would say. About the distribution of primes, there are plenty of them but we don't know how regularly they're distributed. They really behave like a chaotic systems etc and so if π(x)\pi(x) denotes the number of primes up to xx we know how many operands are there, more or less statistically, it's about xlog⁡ x\Large\frac{x}{\log x}\normalsize.

Let π(x)\pi(x) denote the number of primes p<xp < x.

The Prime Number Theorem asserts that
π(x)≈xlog⁡ x\pi(x) \approx \Large\frac{x}{\log x}\normalsize, as x→∞x \rightarrow ∞.
Equivalently, the nn-th prime number pnp_{n} satisfies
pn≈nlog⁡np_{n} \approx n \log n.
So zero density but not that little, I mean only by logarithm xx less than xx, number of prime numbers. This is this is fundamental theorem of number theory, the Prime Number Theorem, the asymptotic formula for number of primes up to xx. Equivalently if you put primes in increasing order, then the nnth prime it behaves like nlog⁡nn \log n asymptotically.

The Riemann Hypothesis asserts that
∣π(x)−∫2x1log⁡ ydy∣≤c√xlog⁡x| \pi(x) - \int _{2}^{x} \large\frac{1}{\log y}\normalsize dy | ≤ c√x \log x. (B Riemann, 1859)
where x≥2x ≥ 2 and cc is a positive constant.

Again I realise that many of you don't capture that, those who are not mathematicians but I hope I can still convey some impressions, so let me continue. This is the Riemann Hypothesis the one, maybe the greatest, open unsolved problem in modern mathematics. The Riemann Hypothesis was originally stated in 1859 by Bernhard Riemann in terms of some complex valued functions and the distribution of zeros but that would be too abstract to talk about here so let me just give you an equivalent statement of that hypothesis, how the prime numbers are distributed. There is a much more precise formula than xlog⁡ x\Large\frac{x}{\log x}\normalsize for π(x)\pi(x) and the precision of the error term in this approximation is about √x√x. That's the content of the Riemann Hypothesis expressed in elementary terms. Maybe not so spectacular a statement but that's what it is, it's the greatest open problem in mathematics that is not solved today. There's a prize for solving this, one million dollars, minus taxes, right.

The Twin Prime Conjecture asserts that there are infinitely many pairs of primes p,qp, q with q=p+2q = p + 2.

For example
(3, 5), (5, 7), (17, 19), (29, 31), ...
It's a hopeless conjecture to try to prove this using tools available today.

All right let's go now to geometry. This is really the beginning of mathematics with Euclid. You know that geometry deals with shapes, positions, dimensions, and other things like this. Everybody intuitively knows what geometry is in high school. You know some theorems, beautiful properties of some figures, geometric figures like Pythagoras' Theorem, right.

3. Geometry

Geometry deals with shapes, positions and dimension of things.

Pythagoras Theorem

32+42=523^{2} + 4^{2}= 5^{2}.


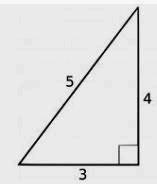
Euclid (From Alexandria, 300 BC) introduced an axiomatic system in his monumental Elements consisting of 13 books.

But Euclid was the first who systematised, compiled the known great theorems of geometry into a system of axioms that he published this in the monumental Elements which consists of certain books. Most of it deals with geometry, some of it about arithmetic as well. What are axioms? The axioms are just the list of facts, of propositions, which are not subject to verification, that are given to us as absolute truths without checking. But they are so simple and obvious, taken from observations that really people don't object, they take it. The idea of axiomatisation is that once you set these axioms as absolute truths, God given so to speak, then the rest comes out by logic, by deduction using logic. It has not much to do with the real world, you see, so in that sense you may say that mathematics is the product of peoples minds once you set up the axioms, it's like art.

Once the axioms are set up the consequences do not necessarily represent the real world.

After that Mathematics is the product of people's minds, like Art.

Well, I don't completely share this viewpoint and I will explain myself later in a different, maybe better, context somehow. So it is true that either we create mathematics or we discover it; that is still a question and people are divided about this viewpoint. Anyway, axioms too in order to be really good should be coherent, they cannot really produce contradictions. They should be complete in the sense that this action should be sufficient by the way of logic to deduce a lot of properties of theorems, new theorems, that we just like or want to describe as real things happening in the world. So also they should be minimalistic in a way that means you should not put into axioms something redundant something that is dispensable. So this is the idea of axiomatisation which is now a practice, common practice, in creating new theorems in mathematics in many other directions. There is a big problem about this position with these axioms.

Euclid's axioms of geometry consisted of five postulates and the fifth one called the Parallel Postulate was questioned. People started to want to deduce it from the other four axioms or to actually prove that it is false but what this says is very simple, right. If you have a line and point not on the line there is exactly one line through this point which does not intersect the given line, that is parallel to the given line in other words.

The Parallel Postulate in Euclidean geometry assumes that for any line and a point not on that line there is exactly one line through this point which doesn't intersect the given line.

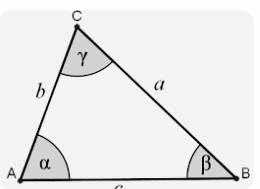
Equivalently, The Sum of Triangle Angles
In a triangle with sides a,b,ca, b, c and angles α,β,γ\alpha, \beta, \gamma
α+β+γ=π\alpha+\beta+\gamma = \pi (= the sum of two right angles)
Area = 12absin⁡γ\large\frac{1}{2}\normalsize ab \sin \gamma.


That is obvious for us, right, but there were people with imagination who had some questions and tried to argue that this may not be always true. You see equivalently you may say this: that this postulate tells you that the sum of angles of triangles they are equal to pi, to two right angles, 180 degrees. We know that from school, right. And just about 200 years ago people start thinking seriously about removing this axiom and replacing it by others. So hyperbolic geometry was created by the assumption that there are infinitely many parallel lines.

Hyperbolic Geometry (Lobachevsky 1829, Bolyai 1832) assumes there are infinitely many "parallel lines".

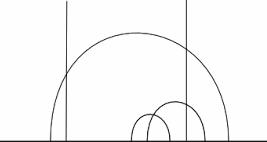
There are lots of models of this hyperbolic geometry known in the literature. I like that so-called Poincaré model. I really have to rush and cannot go into details. I don't know if I'm clear enough. What does a model mean? But let's postpone it or leave it just unclear. So the Poincaré model of hyperbolic geometry is the points are in the upper half plane says the model is just a Euclidean plane but points are in the upper half plane only and there's a different metric than that which is known from Euclidean geometry, hyperbolic metric, and then it gives you concept of straight lines and segments. Lines are just simply connecting points in the shortest possible way. That's how the geodesic line is defined and it happens they are not straight lines, the closest distances between points are along some other curves like half circles orthogonal to the real line, that's the geodesic lines in the Poincaré model of hyperbolic geometry. Triangles look the same but the sides are just a section of the circles, angles are the same and that's a hyperbolic triangle. But what is curious here is that the sum of the angles of a triangle is strictly less than π\pi, not equal to π\pi, and this is because of the curvature this is so-called negative curvature. The space is bent, you know, it's not just flat like that. Now find out what is the deficit. The deficit is just the difference π−α\pi - \alpha, it is just the area of the triangle. This is a beautiful formula in hyperbolic geometry and one thing you have to notice is that the area of a triangle does not depend on the sides of the triangle, on the angles, not like in Euclidean space. Here this is because of the curvature. Other things that are curious I have no time to talk about. How the points are distributed, they measure the density. The hyperbolic area of a domain in the hyperbolic space is mostly concentrated along the boundary so it makes harmonic analysis much harder there than in Euclidean space but it's a much more powerful tool. So, believe it or not, even this kind of geometry, harmonic analysis automatic forms by domain, is used to study prime numbers. But of course most people know that spaces with negative curvature is in general relativity, an ancient theory etc it's a real thing.

Bernhard Riemann (1854) introduced a large variety of geometries, called Riemannian manifolds, in which the distance function is derived from a differential form.

The General Relativity is based on Riemannian geometry with space-time curvature.

Let me speed up because I don't have much time to be more precise. If somebody asks me in a question, I would be delighted to talk more about this. But let's go further into philosophy, logic and set theory. I'm not so sure that philosophy is mathematics but logic and set theory, yes, okay. So one of the questions about arithmetic is the completeness. The completeness means the actions of arithmetic are sufficient to do everything that we dream to get out of it, right, so to speak. Well first of all we have to axiomatise arithmetic. So it was, I think, that the first serious axiomatization of arithmetic was done by Peano who introduced a mathematical induction for example.

4. Philosophy - Logic - Set Theory

Completeness of arithmetic?

Hilbert Formalism - to find a set of axioms sufficient for all mathematics.

This wishful goal of David Hilbert was demolished in the monumental work of Kurt Gödel (1931).

Incompleteness Theorem. Any consistent formal system FF within which elementary arithmetic can be carried out is incomplete. This means a statement can be formulated in the language of FF which cannot be proved or disproved in FF.

So Hilbert, a giant of mathematics, in the history of mathematics, David Hilbert represented this formalism. He was a dreamer. He really wanted a set of axioms which would be sufficient for all mathematics, just a set of axioms for all mathematics, and it was naive in a sense. Its strange for me to say this was naive when the giant of mathematics David Hilbert tried to do it. Anyway his wishful goal was demolished by Kurt Gödel in 1931 who published a paper about an incompleteness theorem. Kurt Gödel, I think, is the number one the logician of all time in the history of mathematics. I will talk about the number two logician in a moment. So what is his theorem roughly speaking? You may not understand my words, this is a really loose statement, it says that for consistent formal systems not only just axioms, you have to also have proper language for it in which all these elementary operations can be done within arithmetic; it is necessarily incomplete. There is no such thing as a complete system in a precise sense. What does it mean it's incomplete? There's nothing wrong, it's just incomplete which means you can formulate a statement in the language of your system which cannot be proved or disproved. Neither proved nor disproved, that's the huge statement of the incompleteness theorem of Kurt Gödel. So the dream of the Hilbert was crashed, okay.

The Polish school of logic has an essential contribution to the history of the subject and I will come to this in a moment later if time permits. But very weird things happen in axiomatic set theory.

Weird things happen in the axiomatic set theory of Zermelo-Fraenkel which accepts the following

Axiom of Choice. Given any collection of non-empty sets (infinite collection) one can select exactly one element from each set.

Set theory was created by Georg Cantor based on this logic. You know what a set is, what sets consist of. You can have elements you can add, you can make a union of sets, you can intersect sets, these kinds of things, right. Axiomatic set theory has many attempts at the right axioms, but the most acclaimed system is by Zermelo-Fraenkel and to extend it with the so-called Axiom of Choice. It's almost embarrassing to talk about it because these axioms are so obvious. Why were people worried? Why do they worry about what the Axiom of Choice says: if you have a collection of non-empty sets, let's say an infinite collection because it's trivial for finite collections, infinite collection of non-empty sets you can pick out exactly one element from each set. I mean this goes without saying, right, it's so obvious. Well luckily for mathematicians it was not obvious. The point is that you don't have a function of choice to choose these elements. Let me give you quickly, I don't have time for details, but quickly tell you how this was illustrated by Bertrand Russell, in a sort of a joke. If you have an infinite collection of pairs of shoes you can select one shoe from each set. For example the shoe for the left foot, it's easy. But if you have an infinite collection of socks you have no way to select one from each collection. So there's a difference, that's the essence of the Axiom of Choice but it is so obvious in a way that people accept it. When you accept it, really really strange things happen by way of logic, you can prove something unbelievable. Here is one example, the Banach-Tarski paradox.

Banach-Tarski Paradox (1924). Any solid ball can be decomposed into a finite number of disjoint pieces which can be reassembled (by moving and rotating without changing their shape) into two copies of the original ball.

What it says is that any solid ball can be decomposed into a finite number of disjoint pieces and then out of these pieces you can reassemble two copies of the same original ball, the same ones with no holes, no empty spaces, no adding any point, just exactly the same ones. But more importantly, oh my god that should really be more importantly, this composition is such that the pieces that you assemble, these pieces with rigid motions by rotating them or pushing them forward and backwards, you don't change the shape, you don't squeeze them, you don't contract them in any way, just isometrically so to speak. This is really a paradox and you get two balls out of one identical one. Imagine these balls are made out of gold, You would produce gold from thin air, you'd like that. Well the point was of course about the measure theory. You know the Axiom of Choice tells you that this exists. It shows you the existence of sets for which you cannot attach a measure like the volume, the area etc, something like that. So this is the paradox and one of the other consequences, a paradox of this Axiom of Choice, is the Continuum Hypothesis.

Continuum Hypothesis. There is no set whose cardinality is strictly between that of the integers and the set of real numbers.

In 1963 Paul Cohen (a student of Antoni Zygmund) showed that CH is independent of ZFC. This means CH can neither be proved nor refuted.

I mentioned that real numbers are a larger set than the integers and in some sense much larger. They are both infinite but one is countable the other is an uncountable set so there is a conjected hypothesis that there is nothing between them in terms of these infinite cardinalities. So that's what the Continuum Hypothesis means and in 1933 Paul Cohen showed that the Continuum Hypothesis is independent of the axioms of Zermelo-Fraenkel and Axiom of Choice. Independent that means that you cannot prove it or disprove it. So you can accept it or not, so that then you have two different worlds, you know, and you can continue your way and depart from your friend who can accept it and you'll reject it. It's up to you to accept that. This is a mathematical statement it's not just simply a loose choice that looks the same within the axioms that have been proposed. By the way Paul Cohen was a student of Antoni Zygmund who was a Polish mathematician. Zygmund worked representing the Warsaw School of Mathematics and was really one of the greatest in his time in analysis, harmonic analysis, Fourier series. He emigrated to Chicago where Paul Cohen was his student. Other people, for example Józef Marcinkiewicz, were also students of Zygmund. I don't really have much time to talk about these individuals. They're very nice people. I was fortunate to meet Cohen personally and I even lived in his house for two weeks. He was a wonderful fellow so he solved the problem of the Continuous Hypothesis; it's just independent of the axioms.

The Principle of Explosion in classical logic asserts that from a false assumption anything follows.

Lwów-Warsaw School of Logic:

Łukasiewicz (1878-1956) : Polish notation
Alfred Tarski (1901-1983). : model theory, metamathematics
Andrzej Mostowski (1913-1975) : undecidability
Helena Rasiowa (1917-1994). : algebraic models

There are other really weird things coming from this kind of axiom in mathematics. One of the sources for ineffective results is this Principle of Explosion that says anything follows from a false assumption. So you can prove anything once you assume something false at the beginning of it. But there is no time to talk about this unless you ask some question asking me to give an example of ineffective results. But anyway I don't have much time about to talk about the Polish school of mathematics but one group of researchers, Warsaw School of Logic, is really powerful, Łukasiewicz, Tarski. Tarski is considered as second greatest after Gödel as a logician of the world of all time. He worked on model theory mathematics. Łukasiewicz earlier, he introduced Polish notation. This terminology is known in the literature. More or less it means he found a logical notation which avoids using brackets etc. Now other great giants of the Polish school of logic were Andrzej Mostowski and Helena Rasiowa and a few others like Jan Kalicki, for example. I have no time to talk about other schools of Polish mathematics like Kraków or Lwów and Warsaw also. Maybe, if time permits, I will make a few more comments. Let me change the subject a little bit from Polish mathematics.

5. Fixed Point Theorems

Under suitable conditions about the map f:X→Xf: X \rightarrow X there is a point x∈Xx \in X such that f(x)=xf(x) = x.

Brouwer (1881-1966) -fixed point theorem and philosophy of intuitionism.

Polish Contribution:

Banach (1892-1945) - founder of modern functional analysis.
Knaster-Tarski - fixed points in lattices
Ryll-Nardzewski (1926-2015),
Schauder (1899-1943, executed by Gestapo).

Well mathematics as a whole has really dominating areas of analysis and topology. Topology is the study of things that look the same after a continuous deformation. For example in topology a cup of coffee with a handle is the same thing topologically as a doughnut, but I don't propose verifying this by tasting. I think doughnuts are nicer to eat and won't crush in your teeth like your cup of coffee. But the cup of coffee and doughnuts are the same topologically; that's what topology is about. So one of the questions in topology is a fixed point problem which means that if you have a map of topological space which is continuous or satisfies certain other conditions, there is a point that is a fixed point, right. So it was started by Brouwer, the Dutch mathematician, who was actually more known as a philosopher of intuitionism, but he did the fixed point business. But the Polish school was really powerful in this.

Borsuk-Ulam Theorem on Antipodal Points.

For every continuous function f:Sn→Rnf: S^{n} \rightarrow \mathbb{R}^{n} there exists x∈Snx \in S^{n} such that f(−x)=f(x)f(-x) = f(x).

Corollary 1. At any time there is a pair of antipodal points on the Earth's equator with the same temperature.

Corollary 2. At any time there is a pair of antipodal points on the Earth's surface with equal temperatures and equal barometric pressures.

So the Polish contribution to fixed point theory, Banach, Tarski, again, Ryll-Nardzewski and Schauder, a tragic figure in Polish mathematics who didn't live long; he was just executed by the Gestapo. Okay, so let me just give you another beautiful application of the fixed point theorem. This is the Borsuk-Ulam theorem of about antipodal points. If you have a continuous transformation of a sphere, a sphere is the surface of a ball, or one dimensional that's just simply a circle, two dimensional will be the surface of a sphere, if you have such a map ff which is continuous without breaking that transforms the surface into Euclidean space then there exists a point xx such that f(−x)=f(x)f(-x) = f(x). −x-x of xx here depicts mathematically the antipodal point to xx, that's a theorem mathematically stated but if you don't like mathematical formulas, okay, here is the corollary in human language. First corollary: at anytime there is a pair of antipodal points on the earth's equator with the same temperature. Isn't that nice. Of course you assume the temperature function is continuous as a function, why not, right. That's in dimension one, S1S^{1}, and that's just a circle, that's the equator of the Earth. Take the dimension two then it is a sphere. Then you consider points on the Earth's surface. You can find a pair of antipodal points, I mean the two points that are most distance apart on the surface of the Earth. So the theorem says there are two points, antipodal points, where at any given time you have the same temperature and the same barometric pressure. Two parameters equal, that is a practical result I think, right. Anyway I don't have much time to talk even more so let me just make a conclusion and save maybe some time for discussion or maybe showing some pictures and photographs.

6. Conclusion

Characters of a mathematician:

- love abstract thinking,
- can identify equivalent structures
- create generalisations,
- can see analogy between different events.

So let me conclude with my own characterisation of our species of mathematicians. So mathematicians love abstract thinking, they can identify equivalent structures like, as I said, the cup of coffee with a handle and the doughnut are the same for mathematician, right. You know they can generalise things. They can see more structures in general terms and they can see analogies between different events. So that's what a mathematician's life is all about. How they visualise, how they live in their own space.

Let me end with two interesting statements, one given by the French mathematician Henri Poincaré. I think he's justly considered the second greatest mathematician who ever lived on this planet. He said:
Mathematics is the art of giving the same name to different things.
Well I see everyone is laughing, so it is laughable, right, but I think it's a very deep statement. Think about it please, okay, think about it, it's not trivial. And now the final statement is by the number one mathematicians of all time, Carl Friedrich Gauss:
Mathematics is the queen of sciences and number theory is the queen of mathematics.
I like that because number theory is my domain.