János Kollár Awards
János Kollár received a number of awards, for example: the Rényi prize for undergraduate research (1978); First prize, M Schweitzer competition (1979); First prize, M Schweitzer competition (1980); University of Utah Distinguished Research Award (1992); the Frank Nelson Cole Prize in Algebra (2006); the Frederic Esser Nemmers Prize in Mathematics (2016); the Shaw Prize in Mathematical Sciences (2017); and János Bolyai International Mathematics Award (2025). We give details below of the four most recent awards.
Click on a link below to go to that award
Click on a link below to go to that award
- Frank Nelson Cole Prize in Algebra (2006)
- Frederic Esser Nemmers Prize (2016)
- Shaw Prize in Mathematical Sciences (2017)
- János Bolyai International Mathematics Award (2025)
1. Frank Nelson Cole Prize in Algebra (2006).
1.1. The Frank Nelson Cole Prize in Algebra.
The Cole Prize in Algebra is awarded every three years by the American Mathematical Society for a notable research memoir in algebra that has appeared during the previous five years (until 2000, the prize was usually awarded every five years). The awarding of this prize alternates with the awarding of the Cole Prize in Number Theory, also given every three years. These prizes were established in 1928 to honour Frank Nelson Cole on the occasion of his retirement as secretary of the American Mathematical Society after twenty-five years of service. He also served as editor-in-chief of the Bulletin for twenty-one years. The Cole Prize carries a cash award of US$5,000.
1.2. The 2006 Frank Nelson Cole Prize in Algebra.
The 2006 Frank Nelson Cole Prize in Algebra was awarded at the 112th Annual Meeting of the American Mathematical Society in San Antonio in January 2006. The Cole Prize in Algebra is awarded by the American Mathematical Society Council acting on the recommendation of a selection committee. For the 2006 prize, the members of the selection committee were: Georgia Benkart (chair), Eric M Friedlander, and Craig L Huneke.
1.3. Citation for János Kollár for 2006 Frank Nelson Cole Prize in Algebra.
The 2006 Cole Prize in Algebra is awarded to János Kollár of Princeton University for his outstanding achievements in the theory of rationally connected varieties and for his illuminating work on a conjecture of Nash.
The notion of a rational variety has long played an important role in algebraic geometry. An algebraic variety X is rationally connected if there are enough rational curves to connect points in X. A pioneer of the notion of rationally connected varieties, Kollár extended the theory from the complex numbers to local fields. His papers (Annals of Math. 150 (1999), 357-367, and Michigan Math. J. 48 (2000), 359-368) and his joint work with Endre Szabó (Duke Math. J. 120 (2003), 251-267) are recognised as significant advancements in the theory of rationally connected varieties.
In 1952, after proving that a compact differentiable manifold M is diffeomorphic to the zero set of real polynomials, John Nash conjectured that there exists a smooth real algebraic variety, birational to projective space, whose real points are diffeomorphic to M. Although known to be false in dimension two, evidence suggested a positive solution in higher dimensions until Kollár provided counterexamples by classifying the diffeomorphism types of smooth threefolds birational to projective space whose real points are orientable. This work is explained in a series of remarkable papers, notably his paper in J. Amer. Math. Soc. 12 (1999), 33-83.
1.4. Biographical Sketch for János Kollár.
János Kollár was born in Budapest, Hungary, in 1956. He did his undergraduate studies at Eötvös University in Budapest and his graduate studies at Brandeis University with Teruhisa Matsusaka. After receiving his doctorate in 1984 he was a Junior Fellow at Harvard University (1984-87) and then a faculty member at the University of Utah (1987-99). Since 1999 he has been a professor at Princeton University.
Kollár was elected to the Hungarian Academy of Sciences in 1995 and to the National Academy of Sciences in 2005. He gave the American Mathematical Society Colloquium Lectures at the New Orleans Annual Meeting in 2001. Kollár's main research area is the birational geometry of higher dimensional algebraic varieties, and he also likes to explore the various applications of algebraic geometry to algebra, combinatorics, complex analysis, differential geometry, and number theory.
1.5. Response from János Kollár.
The most basic algebraic variety is affine -space , and it has been a long-standing problem to understand which varieties behave like . For surfaces the problem was settled by Castelnuovo in the 1890s: these are the surfaces which are birational to . It took nearly a century to understand that the correct higher dimensional concept is not so global. Instead, we should focus on rational curves on varieties. There are plenty of rational curves in : lines, conics, etc. Roughly speaking, a variety is rationally connected if it contains rational curves in similar abundance. It took some time to establish that rationally connected varieties are indeed the right class, but by now it is firmly settled that, at least in characteristic zero, we have the right definition.
I am very glad that the committee recognised the significance of this field and I feel deeply honoured that they chose me to represent a whole area. This was truly a joint effort over the past fifteen years. Much of the foundational work was done with Campana, Miyaoka, and Mori, and the last piece of the basic theory was completed by Graber, Harris, de Jong, and Starr. Arithmetic questions over finite and p-adic fields were explored with Colliot-Thélène, Esnault, Kim, and Szabó, but the theory over global fields consists mostly of questions. Joint work with Bien, Borel, Corti, Schreyer, and Smith touched other aspects of rational connectedness.
The Nash conjecture on the topology of rationally connected varieties over R turned out to be beautiful algebraic geometry in dimension three, and the higher dimensional versions by Eliashberg and Viterbo use techniques from symplectic geometry.
The theory of rationally connected varieties is rapidly growing, with recent major results by Hacon, Hassett, McKernan, Tschinkel, and Zhang. I hope that the recognition by the Cole Prize will spur further activity.
Finally, I would like to thank three mathematicians who had a great influence on my work: my thesis advisor Teruhisa Matsusaka, who taught me to look for the big picture; my collaborator Shigefumi Mori, with whom many of these ideas were developed; and my former colleague Herb Clemens and the University of Utah for providing a wonderful environment to accomplish most of this research.
1.6. Kollár receives American Mathematical Society prize.
János Kollár, professor of mathematics, has been awarded the 2006 Frank Nelson Cole Prize in Algebra by the American Mathematical Society.
Presented every three years, the Cole Prize is one of the highest distinctions in mathematics. Kollár, who specialises in algebraic geometry, is being honoured "for his outstanding achievements in the theory of rationally connected varieties and for his illuminating work on a conjecture of Nash," according to the society.
Kollár was on the faculty of the University of Utah before joining the Princeton faculty in 1999. He was elected to the Hungarian Academy of Sciences in 1995 and to the U.S. National Academy of Sciences in 2005.
2. Frederic Esser Nemmers Prize (2016).
The Cole Prize in Algebra is awarded every three years by the American Mathematical Society for a notable research memoir in algebra that has appeared during the previous five years (until 2000, the prize was usually awarded every five years). The awarding of this prize alternates with the awarding of the Cole Prize in Number Theory, also given every three years. These prizes were established in 1928 to honour Frank Nelson Cole on the occasion of his retirement as secretary of the American Mathematical Society after twenty-five years of service. He also served as editor-in-chief of the Bulletin for twenty-one years. The Cole Prize carries a cash award of US$5,000.
1.2. The 2006 Frank Nelson Cole Prize in Algebra.
The 2006 Frank Nelson Cole Prize in Algebra was awarded at the 112th Annual Meeting of the American Mathematical Society in San Antonio in January 2006. The Cole Prize in Algebra is awarded by the American Mathematical Society Council acting on the recommendation of a selection committee. For the 2006 prize, the members of the selection committee were: Georgia Benkart (chair), Eric M Friedlander, and Craig L Huneke.
1.3. Citation for János Kollár for 2006 Frank Nelson Cole Prize in Algebra.
The 2006 Cole Prize in Algebra is awarded to János Kollár of Princeton University for his outstanding achievements in the theory of rationally connected varieties and for his illuminating work on a conjecture of Nash.
The notion of a rational variety has long played an important role in algebraic geometry. An algebraic variety X is rationally connected if there are enough rational curves to connect points in X. A pioneer of the notion of rationally connected varieties, Kollár extended the theory from the complex numbers to local fields. His papers (Annals of Math. 150 (1999), 357-367, and Michigan Math. J. 48 (2000), 359-368) and his joint work with Endre Szabó (Duke Math. J. 120 (2003), 251-267) are recognised as significant advancements in the theory of rationally connected varieties.
In 1952, after proving that a compact differentiable manifold M is diffeomorphic to the zero set of real polynomials, John Nash conjectured that there exists a smooth real algebraic variety, birational to projective space, whose real points are diffeomorphic to M. Although known to be false in dimension two, evidence suggested a positive solution in higher dimensions until Kollár provided counterexamples by classifying the diffeomorphism types of smooth threefolds birational to projective space whose real points are orientable. This work is explained in a series of remarkable papers, notably his paper in J. Amer. Math. Soc. 12 (1999), 33-83.
1.4. Biographical Sketch for János Kollár.
János Kollár was born in Budapest, Hungary, in 1956. He did his undergraduate studies at Eötvös University in Budapest and his graduate studies at Brandeis University with Teruhisa Matsusaka. After receiving his doctorate in 1984 he was a Junior Fellow at Harvard University (1984-87) and then a faculty member at the University of Utah (1987-99). Since 1999 he has been a professor at Princeton University.
Kollár was elected to the Hungarian Academy of Sciences in 1995 and to the National Academy of Sciences in 2005. He gave the American Mathematical Society Colloquium Lectures at the New Orleans Annual Meeting in 2001. Kollár's main research area is the birational geometry of higher dimensional algebraic varieties, and he also likes to explore the various applications of algebraic geometry to algebra, combinatorics, complex analysis, differential geometry, and number theory.
1.5. Response from János Kollár.
The most basic algebraic variety is affine -space , and it has been a long-standing problem to understand which varieties behave like . For surfaces the problem was settled by Castelnuovo in the 1890s: these are the surfaces which are birational to . It took nearly a century to understand that the correct higher dimensional concept is not so global. Instead, we should focus on rational curves on varieties. There are plenty of rational curves in : lines, conics, etc. Roughly speaking, a variety is rationally connected if it contains rational curves in similar abundance. It took some time to establish that rationally connected varieties are indeed the right class, but by now it is firmly settled that, at least in characteristic zero, we have the right definition.
I am very glad that the committee recognised the significance of this field and I feel deeply honoured that they chose me to represent a whole area. This was truly a joint effort over the past fifteen years. Much of the foundational work was done with Campana, Miyaoka, and Mori, and the last piece of the basic theory was completed by Graber, Harris, de Jong, and Starr. Arithmetic questions over finite and p-adic fields were explored with Colliot-Thélène, Esnault, Kim, and Szabó, but the theory over global fields consists mostly of questions. Joint work with Bien, Borel, Corti, Schreyer, and Smith touched other aspects of rational connectedness.
The Nash conjecture on the topology of rationally connected varieties over R turned out to be beautiful algebraic geometry in dimension three, and the higher dimensional versions by Eliashberg and Viterbo use techniques from symplectic geometry.
The theory of rationally connected varieties is rapidly growing, with recent major results by Hacon, Hassett, McKernan, Tschinkel, and Zhang. I hope that the recognition by the Cole Prize will spur further activity.
Finally, I would like to thank three mathematicians who had a great influence on my work: my thesis advisor Teruhisa Matsusaka, who taught me to look for the big picture; my collaborator Shigefumi Mori, with whom many of these ideas were developed; and my former colleague Herb Clemens and the University of Utah for providing a wonderful environment to accomplish most of this research.
1.6. Kollár receives American Mathematical Society prize.
János Kollár, professor of mathematics, has been awarded the 2006 Frank Nelson Cole Prize in Algebra by the American Mathematical Society.
Presented every three years, the Cole Prize is one of the highest distinctions in mathematics. Kollár, who specialises in algebraic geometry, is being honoured "for his outstanding achievements in the theory of rationally connected varieties and for his illuminating work on a conjecture of Nash," according to the society.
Kollár was on the faculty of the University of Utah before joining the Princeton faculty in 1999. He was elected to the Hungarian Academy of Sciences in 1995 and to the U.S. National Academy of Sciences in 2005.
2.1. The Frederic Esser Nemmers Prize in Mathematics.
The $300,000 Frederic Esser Nemmers Prize in Mathematics is awarded by Northwestern University for achievement and work of lasting significance in the field of mathematics. The prize was established in 1994. Recipients of the Frederic Esser Nemmers Prize present lectures, participate in department seminars, and engage with Northwestern faculty and students in other scholarly activities.
The Nemmers prizes are made possible through bequests from the late Erwin Esser Nemmers, a former member of the Northwestern University faculty, and his brother, the late Frederic E Nemmers, both of Milwaukee. Each prize is awarded every other year.
Erwin Nemmers, who persuaded his brother to join him in making a substantial contribution to Northwestern, served as a member of the faculty of the Kellogg School of Management from 1957 until his retirement in 1986. He and Frederic Nemmers were principals in a Milwaukee-based, family-owned, church music publishing house.
Their gifts, totalling $14 million, were designated by Erwin and Frederic Nemmers for the establishment of the Nemmers prizes and the establishment of four endowed professorships in the Kellogg School of Management.
Consistent with the terms of the Nemmers' bequests, the Frederic Esser Nemmers Prize in Mathematics (named by Erwin in honour of his brother) is awarded for "achievement and work of lasting significance in mathematics."
2.2. The 2016 Frederic Esser Nemmers Prize in Mathematics.
The 2016 Frederic Esser Nemmers Prize in Mathematics was awarded to János Kollár, the Donner Professor of Science and Professor of Mathematics at Princeton University:-
Northwestern University announced the recipient of the 2016 Frederic Esser Nemmers Prize in Mathematics on 7 April 2016. The prizes are awarded every other year in recognition of major contributions to new knowledge or the development of significant new modes of analysis.
Kollár was selected for his "fundamental contributions to algebraic geometry, including the minimal model program and its applications, the theory of rational connectedness and the study of real algebraic varieties."
"János Kollár is an original thinker in mathematics, and it is an extraordinary privilege for Northwestern to recognise him for his significant contributions," Northwestern Provost Daniel Linzer said. "We look forward to having him on campus, sharing his knowledge and interacting with the University community."
In connection with the Nemmers award, Kollár will deliver a public lecture and participate in other scholarly activities at Northwestern during the 2016-17 and 2017-18 academic years.
The prize carries a $200,000 stipend, among the largest monetary awards in the United States for outstanding achievements in mathematics. This year marks the 12th time Northwestern has awarded the prize.
2.4. János Kollár: 2016 Frederic Esser Nemmers Prize in Mathematics.
Kollár's specialty is algebraic geometry with additional interest in related questions in number theory, complex geometry and commutative algebra.
He is well known for his contributions to the minimal model program for threefolds, for pioneering the notion of rational connectedness and for finding counterexamples to a conjecture of the late John Nash. In 1952, Nash conjectured a converse to a famous theorem he proved; Kollár was able to provide many three-dimensional counterexamples from an important new structure theory for a class of three-dimensional algebraic varieties.
The recipient of numerous honours during his career, Kollár was elected to the U.S. National Academy of Sciences in 2005 and the Hungarian Academy of Sciences in 1995. He became a fellow of the American Mathematical Society (AMS) in 2012. Kollár received the 2006 Frank Nelson Cole Prize in Algebra from the AMS, one of the highest distinctions in mathematics. He also was named a Presidential Young Investigator in 1988 and a Sloan Foundation Fellow in 1989.
Kollár was a plenary speaker at the International Congress of Mathematicians held in 2014 in Seoul. In 1996, he gave one of the plenary addresses at the European Mathematical Congress in Budapest. In 1990, Kollár was an invited speaker at the International Congress of Mathematicians in Kyōto.
Kollár is the author of more than 130 articles and five monographs in algebraic geometry. He serves as editor of several journals, including the Algebra and Number Theory and the Duke Mathematics Journal.
A native of Hungary, Kollár began his studies at the Eötvös University in Budapest and later received his Ph.D. from Brandeis University in 1984 with Teruhisa Matsusaka. He was a Junior Fellow at Harvard from 1984 to 1987 and a professor at the University of Utah before joining the Princeton faculty in 1999. Kollár currently is the associate chair of Princeton's department of mathematics.
2.5. Professor János Kollár Receives 2016 Nemmers Prize and is Named Fellow of the American Academy of Arts and Sciences.
Congratulations to Professor Kollár, who has been awarded the 2016 Frederic Esser Nemmers Mathematics Prize for "his fundamental contributions to algebraic geometry, including the minimal model program and its applications, the theory of rational connectedness and the study of real algebraic varieties." The Nemmers Prizes are awarded every other year by Northwestern University in the fields of Economics, Mathematics, Medical Sciences, and Music. Past recipients include Ingrid Daubechies, Princeton Professor from 1994 to 2010; Terrance Tao *96; Professor Yakov Sinai; and Professor John Conway.
Separately, Professor Kollár was elected to the 2016 class of Fellows of the American Academy of Arts and Sciences. This year 213 new members were elected to the Academy, including 6 other Princeton faculty members from other departments.
3. Shaw Prize in Mathematical Sciences (2017).
The $300,000 Frederic Esser Nemmers Prize in Mathematics is awarded by Northwestern University for achievement and work of lasting significance in the field of mathematics. The prize was established in 1994. Recipients of the Frederic Esser Nemmers Prize present lectures, participate in department seminars, and engage with Northwestern faculty and students in other scholarly activities.
The Nemmers prizes are made possible through bequests from the late Erwin Esser Nemmers, a former member of the Northwestern University faculty, and his brother, the late Frederic E Nemmers, both of Milwaukee. Each prize is awarded every other year.
Erwin Nemmers, who persuaded his brother to join him in making a substantial contribution to Northwestern, served as a member of the faculty of the Kellogg School of Management from 1957 until his retirement in 1986. He and Frederic Nemmers were principals in a Milwaukee-based, family-owned, church music publishing house.
Their gifts, totalling $14 million, were designated by Erwin and Frederic Nemmers for the establishment of the Nemmers prizes and the establishment of four endowed professorships in the Kellogg School of Management.
Consistent with the terms of the Nemmers' bequests, the Frederic Esser Nemmers Prize in Mathematics (named by Erwin in honour of his brother) is awarded for "achievement and work of lasting significance in mathematics."
2.2. The 2016 Frederic Esser Nemmers Prize in Mathematics.
The 2016 Frederic Esser Nemmers Prize in Mathematics was awarded to János Kollár, the Donner Professor of Science and Professor of Mathematics at Princeton University:-
... for his fundamental contributions to algebraic geometry, including the minimal model program and its applications, the theory of rational connectedness and the study of real algebraic varieties.2.3. Announcement of the 2016 Frederic Esser Nemmers Prize in Mathematics.
Northwestern University announced the recipient of the 2016 Frederic Esser Nemmers Prize in Mathematics on 7 April 2016. The prizes are awarded every other year in recognition of major contributions to new knowledge or the development of significant new modes of analysis.
Kollár was selected for his "fundamental contributions to algebraic geometry, including the minimal model program and its applications, the theory of rational connectedness and the study of real algebraic varieties."
"János Kollár is an original thinker in mathematics, and it is an extraordinary privilege for Northwestern to recognise him for his significant contributions," Northwestern Provost Daniel Linzer said. "We look forward to having him on campus, sharing his knowledge and interacting with the University community."
In connection with the Nemmers award, Kollár will deliver a public lecture and participate in other scholarly activities at Northwestern during the 2016-17 and 2017-18 academic years.
The prize carries a $200,000 stipend, among the largest monetary awards in the United States for outstanding achievements in mathematics. This year marks the 12th time Northwestern has awarded the prize.
2.4. János Kollár: 2016 Frederic Esser Nemmers Prize in Mathematics.
Kollár's specialty is algebraic geometry with additional interest in related questions in number theory, complex geometry and commutative algebra.
He is well known for his contributions to the minimal model program for threefolds, for pioneering the notion of rational connectedness and for finding counterexamples to a conjecture of the late John Nash. In 1952, Nash conjectured a converse to a famous theorem he proved; Kollár was able to provide many three-dimensional counterexamples from an important new structure theory for a class of three-dimensional algebraic varieties.
The recipient of numerous honours during his career, Kollár was elected to the U.S. National Academy of Sciences in 2005 and the Hungarian Academy of Sciences in 1995. He became a fellow of the American Mathematical Society (AMS) in 2012. Kollár received the 2006 Frank Nelson Cole Prize in Algebra from the AMS, one of the highest distinctions in mathematics. He also was named a Presidential Young Investigator in 1988 and a Sloan Foundation Fellow in 1989.
Kollár was a plenary speaker at the International Congress of Mathematicians held in 2014 in Seoul. In 1996, he gave one of the plenary addresses at the European Mathematical Congress in Budapest. In 1990, Kollár was an invited speaker at the International Congress of Mathematicians in Kyōto.
Kollár is the author of more than 130 articles and five monographs in algebraic geometry. He serves as editor of several journals, including the Algebra and Number Theory and the Duke Mathematics Journal.
A native of Hungary, Kollár began his studies at the Eötvös University in Budapest and later received his Ph.D. from Brandeis University in 1984 with Teruhisa Matsusaka. He was a Junior Fellow at Harvard from 1984 to 1987 and a professor at the University of Utah before joining the Princeton faculty in 1999. Kollár currently is the associate chair of Princeton's department of mathematics.
2.5. Professor János Kollár Receives 2016 Nemmers Prize and is Named Fellow of the American Academy of Arts and Sciences.
Congratulations to Professor Kollár, who has been awarded the 2016 Frederic Esser Nemmers Mathematics Prize for "his fundamental contributions to algebraic geometry, including the minimal model program and its applications, the theory of rational connectedness and the study of real algebraic varieties." The Nemmers Prizes are awarded every other year by Northwestern University in the fields of Economics, Mathematics, Medical Sciences, and Music. Past recipients include Ingrid Daubechies, Princeton Professor from 1994 to 2010; Terrance Tao *96; Professor Yakov Sinai; and Professor John Conway.
Separately, Professor Kollár was elected to the 2016 class of Fellows of the American Academy of Arts and Sciences. This year 213 new members were elected to the Academy, including 6 other Princeton faculty members from other departments.
3.1. The Shaw Prizes.
In 2002, under the auspice of Run Run Shaw, a visionary philanthropist, the Shaw Prize Foundation was established. The inaugural Shaw Prize was presented two years later in 2004. The Shaw Prize consists of three annual awards, namely the Prize in Astronomy, the Prize in Life Science and Medicine, and the Prize in Mathematical Sciences. Each of these awards carries the amount of one million dollars.
The Shaw Prize honours individuals, regardless of race, nationality, gender, and religious belief, who are currently active in their respective fields and who have recently achieved distinguished and significant advances, who have made outstanding contributions in academic and scientific research or applications, or who in other domains have achieved excellence. The Shaw Prize is dedicated to furthering societal progress, enhancing quality of life, and enriching humanity's spiritual civilisation.
The Shaw Prize Certificate presented to each laureate is mounted elegantly on a dark brown leather folder. Within the folder, the left side features a decorative rendering, displaying the Shaw Prize medal in relief, and the motto of the Prize, "for the benefit of humankind", in gold engraving. The decoration comes in three distinct colours, each representing one of the award categories. For mathematics, the colour is red. On the certificate, "The Shaw Prize in Mathematical Sciences", engraved in gold, is displayed prominently. Below is the name of the laureate, meticulously handwritten by a local calligrapher, followed by the citation and the date of the award. Each certificate is signed by the Chair of the Board of Adjudicators and the Chair of the Shaw Prize Council.
3.2. The 2017 Shaw Prize in Mathematical Sciences.
The Shaw Prize in Mathematical Sciences 2017 is awarded in equal shares to János Kollár, Professor of Mathematics, Princeton University, USA and Claire Voisin, Professor and Chair in Algebraic Geometry, Collège de France, for their remarkable results in many central areas of algebraic geometry, which have transformed the field and led to the solution of long-standing problems that had appeared out of reach.
3.3. About János Kollár.
János Kollár was born in 1956 in Budapest, Hungary and is currently a Professor of Mathematics at Princeton University, USA. He obtained his Bachelor of Science from Eötvös Loránd University, Hungary in 1980 and his PhD from Brandeis University, USA in 1984. He was a Research Assistant at the Hungarian Academy of Sciences (1980-1981) and Junior Fellow at Harvard University, USA (1984-1987). He joined the University of Utah, USA, where he was successively Associate Professor (1987-1990), Professor (1990-1994) and Distinguished Professor (1994-1999). From 1999, he moved to Princeton University, USA as Professor and was appointed Donner Professor of Science since 2009. He is a member of the US National Academy of Sciences and a Fellow of the American Academy of Arts and Sciences.
3.4. The contribution of János Kollár and Claire Voisin.
Since ancient times, a central theme in mathematics has been the study of polynomials and their solutions. Algebraic geometry is the study of the properties of sets of solutions to polynomial equations in several variables. A simple example of such an equation is , the solution set of which is the surface of a sphere of radius 1.
As this example demonstrates, solution sets of polynomial equations, which are known as varieties, are geometric objects. Examining the interplay between the algebra and the geometry has turned out to be remarkably fruitful, and algebraic geometry is a major branch of mathematics, the study of which has profound consequences not just for algebra and geometry, but also for several other areas ranging from number theory to mathematical physics.
Two varieties are said to be birationally equivalent if they become the same after excluding a suitably small subset. Rational varieties are those that are birationally equivalent to ordinary -dimensional space, for some . Some of the most exciting advances in algebraic geometry over the past few decades have been in better understanding the birational classification of higher-dimensional varieties. For example, Shigefumi Mori won the Fields Medal for his Minimal Model Program. Some of the most important breakthroughs have been in characterising rational varieties. Both János Kollár and Claire Voisin have made central contributions to this development.
Along with his work on birational classification, Kollár's most recent work stands out in a direction that will influence algebraic geometry deeply in the decades to come, as an important complement of the Minimal Model Program: the definition and study of moduli of higher-dimensional varieties, which can be thought of as sophisticated geometrical structures whose points represent equivalence classes of these varieties. The importance of this area can be seen in the immense wealth of papers on the moduli problem in dimension 1, which today occupies topologists, combinatorialists and, perhaps most of all, physicists. Already for surfaces the treatment of moduli is an extremely subtle and difficult problem. Kollár's ideas have almost defined the field of higher-dimensional moduli.
Among Voisin's major achievements is the solution of the Kodaira problem, which starts with the observation that every deformation of a complex projective manifold is a Kähler manifold (which roughly speaking means a geometric set that locally has a structure compatible with the complex numbers) and asks whether the converse is true. She found counterexamples: that is, Kähler manifolds that not only fail to be deformations of projective manifolds but are not even topologically equivalent to projective manifolds. Another of Voisin's pioneering accomplishments is the establishment a new technique for showing that a variety is not rational, a breakthrough that has led to results that would previously have been unthinkable. A third remarkable result is a counterexample to an extension of the Hodge conjecture, one of the hardest problems in mathematics (being one of the Clay Mathematical Institute's seven Millennium Problems); the counterexample rules out several approaches to the conjecture.
The Shaw Prize Mathematical Sciences Selection Committee
23 May 2017
Hong Kong
3.5. Essay on the 2017 Shaw Prize.
Since ancient times, a central theme in mathematics has been the study of polynomials and their solutions. Algebraic geometry is the study of the properties of sets of solutions to polynomial equations in several variables. A simple example of such an equation is , the solution set of which is the surface of a sphere of radius 1.
As this example demonstrates, solution sets of polynomial equations, which are known as varieties, are geometric objects. Examining the interplay between the algebra and the geometry has turned out to be remarkably fruitful, and algebraic geometry is a major branch of mathematics, the study of which has profound consequences not just for algebra and geometry but also for several other areas ranging from number theory to mathematical physics.
For each type of mathematical structure, there is normally a notion of when two examples are essentially the same. For varieties, the notion is called birational equivalence: two varieties are said to be birationally equivalent if, after removing lower-dimensional subvarieties if necessary, there is a rational map from one to the other with a rational inverse. (A rational map is a ratio of two polynomials.) Rational varieties are those that are birationally equivalent to ordinary -dimensional space, for some . To give an example, for every real number one can check that , from which it follows that the map that takes a real number to the point sends an infinite line to the unit circle. One can check further that sending a point in the unit circle to the real number inverts this map. There is a small problem here in that no value of maps to the point (0, -1), but this point on its own is a zero-dimensional subset, which we are allowed to ignore. Thus, a circle is birationally equivalent to ordinary 1-dimensional space, which means that it is a rational variety.
Some of the most exciting advances in algebraic geometry over the past few decades have been in better understanding the birational classification of higher-dimensional varieties. For example, Shigefumi Mori won the Fields Medal for his "Minimal Model Program", which attempts to find in each birational equivalence class a unique simplest variety. There have also been very important breakthroughs in characterising rational varieties: that is, in finding ways of telling whether a variety is rational.
Along with his work on birational classification, Kollár's most recent work stands out in a direction that will greatly affect algebraic geometry in the decades to come, as an important complement of the Minimal Model Program: the definition and study of moduli of higher-dimensional varieties, which can be thought of as sophisticated geometrical structures whose points represent equivalence classes of these varieties. The importance of this area can be seen in the immense wealth of papers on the moduli problem in dimension 1, which today occupies topologists, combinatorialists and, perhaps most of all, physicists. Already for surfaces the treatment of moduli is an extremely subtle and difficult problem. Kollár's ideas have almost defined the field of higher-dimensional moduli.
Among Voisin's major achievements is the solution of the Kodaira problem, which starts with the observation that every deformation of a complex projective manifold is a Kähler manifold (which roughly speaking means a geometric set that locally has a structure compatible with the complex numbers) and asks whether the converse is true. She found counterexamples: that is, Kähler manifolds that do not just fail to be deformations of projective manifolds but are not even topologically equivalent to projective manifolds. Another of Voisin's pioneering accomplishments is the establishment a new technique for showing that a variety is not rational, a breakthrough that has led to results that would previously have been unthinkable. A third remarkable result is a counterexample to an extension of the Hodge conjecture, one of the hardest problems in mathematics (it is one of the Clay Mathematical Institute's seven Millennium Problems), which rules out several approaches to the conjecture.
Algebraic geometry is a central area of mathematics that has seen many remarkable developments in its history, and these developments continue to the present day. In their different ways, János Kollár and Claire Voisin have made profound contributions to algebraic geometry that will deeply influence the future of the subject.
26 September 2017
Hong Kong
3.6. János Kollár autobiography.
I was born in 1956 in Budapest, Hungary, the oldest of six children in a close family full of engineers and musicians. I was a bookish child, interested mostly in history, adventure stories and the sciences. Around age eight I developed a strong stammer, which further led me to reading. The stammering gradually subsided over the next fifteen years, but hints of it remain with me, especially when I am tired of giving talks.
In elementary school I was an undistinguished student, getting middling grades in many classes but doing well in the few that interested me. Luckily my parents had confidence in me, and for high school sent me to the Piarist Fathers. Their school, called the Budapesti Piarista Gimnázium, was founded in 1717. During the communist years it was barely tolerated by the government, but it was probably the best school in Hungary. After getting many failing grades in the first weeks, I came to understand that I had to work hard, and by the end of the first year I was near the top of my class. This was really the experience that started me on the path toward knowledge and science. My two most influential teachers were János Pogány, who taught mathematics, and Zoltán Fórián-Szabó, who taught physics and chemistry.
It was also at this time that I got involved in mathematics competitions. These had a long tradition in Hungary; the first competition for high school students was established in 1894. Those who did well were invited to participate in a monthly meeting where we worked on developing our problem-solving skills. This was a great opportunity to meet other students who were also interested in mathematics, and spur each other on to do better. Each year the best of us were sent to the International Mathematical Olympiad. I was selected twice and returned with a gold medal both times.
After a year of mandatory military service, I enrolled in Eötvös Loránd University in Budapest as a mathematics student. Here I was mostly influenced in my first year by László Babai and later by Ervin Fried. They told me that there was this large branch of mathematics, called algebraic geometry, which was completely unknown in Hungary at that time. So I decided to learn it. For two years I worked completely alone, with only a few books. It was slow going, with nobody to consult, but it resulted in my learning the foundations very well. After that I spent two semesters in Moscow as an exchange student, where I attended the lectures of Iskovskikh and Manin, and the seminar of Shafarevich. At the end of university I applied to enter the PhD programme in Moscow. I had strong support from the Russian mathematicians, but, to my surprise, the examiner failed me on the required Marxism-Leninism exam. I was very disheartened, but this turned out to be one of the great lucky twists in my life.
I had met David Eisenbud when he visited Hungary during my undergraduate years, so when Moscow fell through I wrote to him, asking to be a student in the USA. This was somewhat illegal at that time, so my whole application consisted of that letter. He arranged for a full scholarship for me, and in 1981 I arrived at Brandeis University, where I studied with Teruhisa Matsusaka. He taught me to aim to be not only a technician but a scientist, maybe even a natural philosopher. It was also there that I met my wife, Jennifer Johnson.
I graduated in 1984 and started a Junior Fellowship at Harvard. The Fellowship gave me an opportunity to spend three months in Nagoya and begin my collaboration with Shigefumi Mori. This turned out to have a decisive influence on my work, both in our joint papers, books and in my work ever since.
In 1987 I accepted an invitation from Herb Clemens and joined the mathematics department at the University of Utah in Salt Lake City. The next twelve years were very fruitful, with several visits by Mori, Miyaoka, Voisin, and three intense Summer Seminars where dozens of young algebraic geometers came together to work on the rapidly developing minimal model programme, the moduli theory of canonical models and the early stages of the study of rationally connected varieties. These three topics have been the main areas of my research ever since. It is also in Salt Lake City that our daughter Alicia was born; she is currently a Postdoc at Princeton in experimental physics.
In 1999 we moved to Princeton University, where we have been ever since. Since then I have learned the most from my students, especially from ongoing collaborations with Alessio Corti, Sándor Kovács and Chenyang Xu. I hope to continue learning for many years to come.
26 September 2017
Hong Kong
3.7. Kollár receives 2017 Shaw Prize in mathematics.
János Kollár, the Donner Professor of Science and professor of mathematics at Princeton University, is a co-recipient of the 2017 Shaw Prize in mathematical sciences. Awarded by the Hong Kong-based Shaw Foundation, the Shaw Prize honours recent breakthroughs by researchers in the fields of mathematics, astronomy, and life science and medicine.
Kollár will share the $1.2 million prize with Claire Voisin, a professor and chair in algebraic geometry at the Collège de France. Kollár and Voisin were recognized for their "remarkable results in many central areas of algebraic geometry, which have transformed the field and led to the solution of long-standing problems that had appeared out of reach," according to the prize citation. The 2017 prizes will be awarded during a Sept. 26 ceremony in Hong Kong.
Kollár joined the Princeton faculty in 1999. Among his many honors, he became a member of the National Academy of Sciences in 2005 and an external member of the Hungarian Academy of Sciences in 1995. He received the Cole Prize in Algebra in 2006 and was named a Simons Fellow in Mathematics in 2012 and a fellow of the American Mathematical Society in 2013. He received his Ph.D. from Brandeis University and his B.S. from Eötvös L University in Hungary.
Media mogul and philanthropist Run Run Shaw founded the Shaw Prize in 2002. Other current Princeton faculty who have received the Shaw Prize include: Bonnie Bassler, the Squibb Professor in Molecular Biology and chair of the Department of Molecular Biology who received the 2015 Shaw Prize in life science and medicine; and Lyman Page, the Henry De Wolf Smyth Professor of Physics, and David Spergel, the Charles A Young Professor of Astronomy on the Class of 1897 Foundation, who received the 2010 Shaw Prize in astronomy. P James Peebles, the Albert Einstein Professor of Science, Emeritus, and professor of physics, emeritus, was awarded the 2004 Shaw Prize in astronomy.
3.8. János Kollár: Laureate Video
Diana Lin: The 2017 Shaw Prize in Mathematical Sciences is shared by two algebraic geometers whose amazing results in many key areas transformed their field and led to solutions to long standing problems that had seemed unreachable.
Chris Lincoln: When János Kollár flies into Kong Kong for the Shaw Prize ceremony he'll likely look up at the roof of the passenger terminal. He sees patterns of elliptical lines.
János Kollár: I worked on exactly understanding the type of surfaces that are made up of 2, 3 or more grids of ellipses.
Chris Lincoln: János has been in the mathematics department at Princeton University for 18 years. Before that he spent a dozen years at the University of Utah.
János Kollár: I'm especially interested in the cases where the shape is very sensitive to small changes of the numbers.
Chris Lincoln: Like the Lemniscate of Bernoulli.
János Kollár: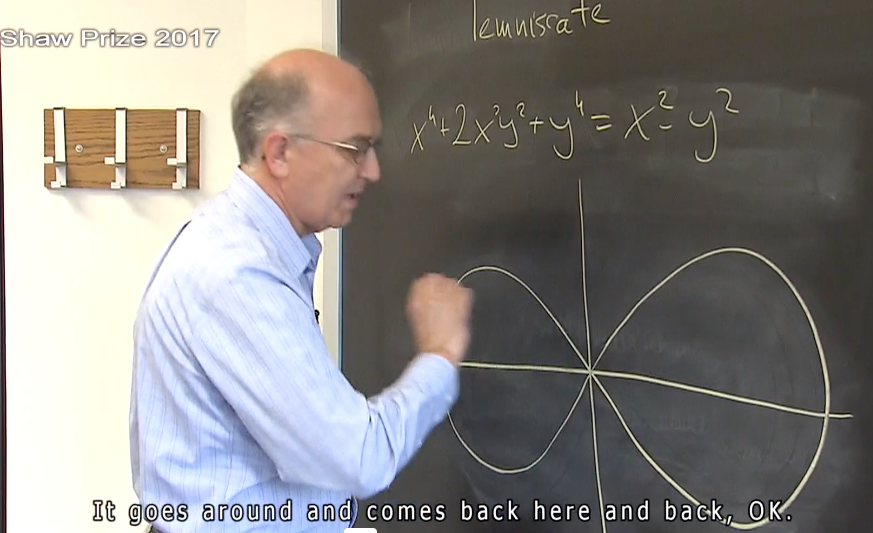
Consider
.
It looks like a nice figure of eight. It goes around and comes back here and back, OK.
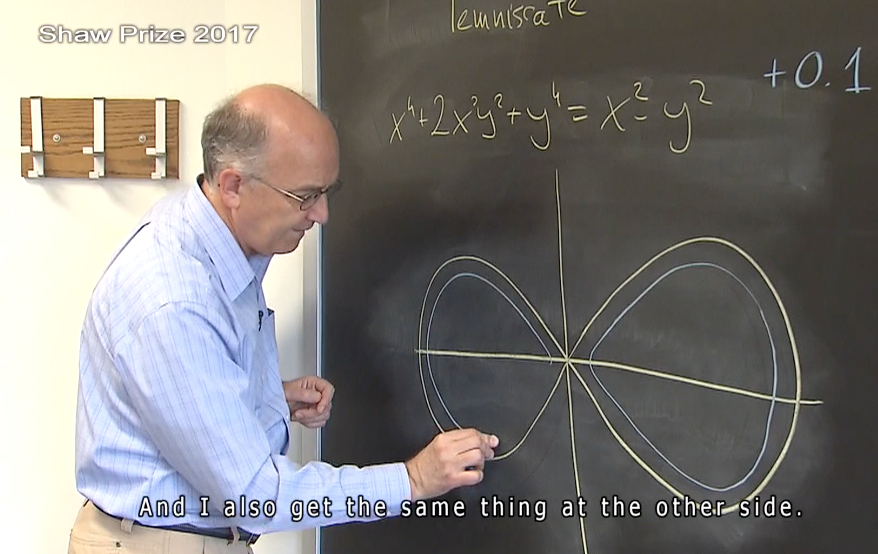
What happens if I add to it a plus zero point one?
Turns out I get something that hugs the figure eight from the inside. So I get something like this. And I also get the same thing at the other side.
Instead of being made out of just one piece of matter, its suddenly made out of two pieces.

Chris Lincoln: And the blue lines don't intersect.
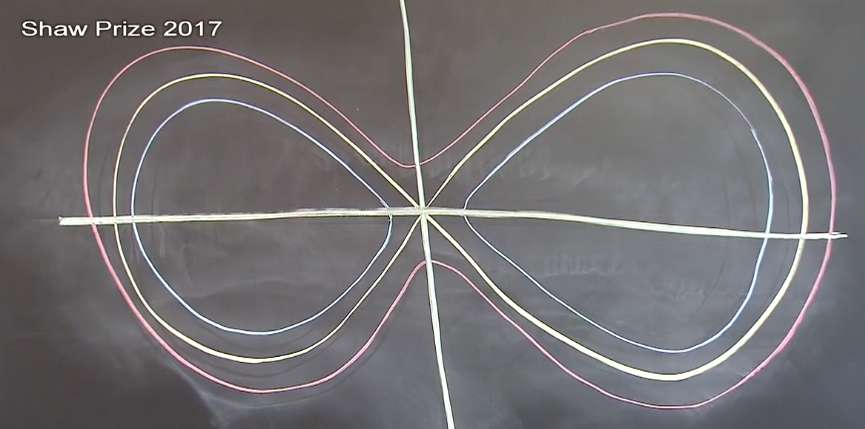
János Kollár: What happens if I subtract zero point one from it?
Well then again I get something that will hug the figure 8 but this time it will hug it from the outside. It doesn't have this part where it intersects.
You can think of it as a circle where you're trying to bring the top and the bottom together.
Nicholas Katz: This idea of what he calls rationally connected varieties, which he wrote a whole book about, that was a brand new insight.
Richard Taylor: He disproved a very longstanding conjecture of John Nash, who both won a Nobel Prize in Economics and an Abel Prize.
Chris Lincoln: As a graduate student at Brandeis University, János met his future wife Jennifer, who is also now a mathematician at Princeton.
Jennifer Johnson: When he's working I can't think about anything else because it looks like something is going to explode over there and this can go on for quite a while.
János Kollár: I'm attacked by mathematics. Then for 3 weeks, I'm ill.
Chris Lincoln: János is the only member of his family in North America. He left his native Hungary after university. János is surrounded by engineers. That includes his brother Peter, his parents, and now his daughter, Alicia, an electrical engineer.
János Kollár: What I especially like is when I teach a class of non-mathematicians and then at the end of the year one or two students usually come to me and say "I would like to be a mathematician now."
4. János Bolyai International Mathematics Award (2025).
In 2002, under the auspice of Run Run Shaw, a visionary philanthropist, the Shaw Prize Foundation was established. The inaugural Shaw Prize was presented two years later in 2004. The Shaw Prize consists of three annual awards, namely the Prize in Astronomy, the Prize in Life Science and Medicine, and the Prize in Mathematical Sciences. Each of these awards carries the amount of one million dollars.
The Shaw Prize honours individuals, regardless of race, nationality, gender, and religious belief, who are currently active in their respective fields and who have recently achieved distinguished and significant advances, who have made outstanding contributions in academic and scientific research or applications, or who in other domains have achieved excellence. The Shaw Prize is dedicated to furthering societal progress, enhancing quality of life, and enriching humanity's spiritual civilisation.
The Shaw Prize Certificate presented to each laureate is mounted elegantly on a dark brown leather folder. Within the folder, the left side features a decorative rendering, displaying the Shaw Prize medal in relief, and the motto of the Prize, "for the benefit of humankind", in gold engraving. The decoration comes in three distinct colours, each representing one of the award categories. For mathematics, the colour is red. On the certificate, "The Shaw Prize in Mathematical Sciences", engraved in gold, is displayed prominently. Below is the name of the laureate, meticulously handwritten by a local calligrapher, followed by the citation and the date of the award. Each certificate is signed by the Chair of the Board of Adjudicators and the Chair of the Shaw Prize Council.
3.2. The 2017 Shaw Prize in Mathematical Sciences.
The Shaw Prize in Mathematical Sciences 2017 is awarded in equal shares to János Kollár, Professor of Mathematics, Princeton University, USA and Claire Voisin, Professor and Chair in Algebraic Geometry, Collège de France, for their remarkable results in many central areas of algebraic geometry, which have transformed the field and led to the solution of long-standing problems that had appeared out of reach.
3.3. About János Kollár.
János Kollár was born in 1956 in Budapest, Hungary and is currently a Professor of Mathematics at Princeton University, USA. He obtained his Bachelor of Science from Eötvös Loránd University, Hungary in 1980 and his PhD from Brandeis University, USA in 1984. He was a Research Assistant at the Hungarian Academy of Sciences (1980-1981) and Junior Fellow at Harvard University, USA (1984-1987). He joined the University of Utah, USA, where he was successively Associate Professor (1987-1990), Professor (1990-1994) and Distinguished Professor (1994-1999). From 1999, he moved to Princeton University, USA as Professor and was appointed Donner Professor of Science since 2009. He is a member of the US National Academy of Sciences and a Fellow of the American Academy of Arts and Sciences.
3.4. The contribution of János Kollár and Claire Voisin.
Since ancient times, a central theme in mathematics has been the study of polynomials and their solutions. Algebraic geometry is the study of the properties of sets of solutions to polynomial equations in several variables. A simple example of such an equation is , the solution set of which is the surface of a sphere of radius 1.
As this example demonstrates, solution sets of polynomial equations, which are known as varieties, are geometric objects. Examining the interplay between the algebra and the geometry has turned out to be remarkably fruitful, and algebraic geometry is a major branch of mathematics, the study of which has profound consequences not just for algebra and geometry, but also for several other areas ranging from number theory to mathematical physics.
Two varieties are said to be birationally equivalent if they become the same after excluding a suitably small subset. Rational varieties are those that are birationally equivalent to ordinary -dimensional space, for some . Some of the most exciting advances in algebraic geometry over the past few decades have been in better understanding the birational classification of higher-dimensional varieties. For example, Shigefumi Mori won the Fields Medal for his Minimal Model Program. Some of the most important breakthroughs have been in characterising rational varieties. Both János Kollár and Claire Voisin have made central contributions to this development.
Along with his work on birational classification, Kollár's most recent work stands out in a direction that will influence algebraic geometry deeply in the decades to come, as an important complement of the Minimal Model Program: the definition and study of moduli of higher-dimensional varieties, which can be thought of as sophisticated geometrical structures whose points represent equivalence classes of these varieties. The importance of this area can be seen in the immense wealth of papers on the moduli problem in dimension 1, which today occupies topologists, combinatorialists and, perhaps most of all, physicists. Already for surfaces the treatment of moduli is an extremely subtle and difficult problem. Kollár's ideas have almost defined the field of higher-dimensional moduli.
Among Voisin's major achievements is the solution of the Kodaira problem, which starts with the observation that every deformation of a complex projective manifold is a Kähler manifold (which roughly speaking means a geometric set that locally has a structure compatible with the complex numbers) and asks whether the converse is true. She found counterexamples: that is, Kähler manifolds that not only fail to be deformations of projective manifolds but are not even topologically equivalent to projective manifolds. Another of Voisin's pioneering accomplishments is the establishment a new technique for showing that a variety is not rational, a breakthrough that has led to results that would previously have been unthinkable. A third remarkable result is a counterexample to an extension of the Hodge conjecture, one of the hardest problems in mathematics (being one of the Clay Mathematical Institute's seven Millennium Problems); the counterexample rules out several approaches to the conjecture.
The Shaw Prize Mathematical Sciences Selection Committee
23 May 2017
Hong Kong
3.5. Essay on the 2017 Shaw Prize.
Since ancient times, a central theme in mathematics has been the study of polynomials and their solutions. Algebraic geometry is the study of the properties of sets of solutions to polynomial equations in several variables. A simple example of such an equation is , the solution set of which is the surface of a sphere of radius 1.
As this example demonstrates, solution sets of polynomial equations, which are known as varieties, are geometric objects. Examining the interplay between the algebra and the geometry has turned out to be remarkably fruitful, and algebraic geometry is a major branch of mathematics, the study of which has profound consequences not just for algebra and geometry but also for several other areas ranging from number theory to mathematical physics.
For each type of mathematical structure, there is normally a notion of when two examples are essentially the same. For varieties, the notion is called birational equivalence: two varieties are said to be birationally equivalent if, after removing lower-dimensional subvarieties if necessary, there is a rational map from one to the other with a rational inverse. (A rational map is a ratio of two polynomials.) Rational varieties are those that are birationally equivalent to ordinary -dimensional space, for some . To give an example, for every real number one can check that , from which it follows that the map that takes a real number to the point sends an infinite line to the unit circle. One can check further that sending a point in the unit circle to the real number inverts this map. There is a small problem here in that no value of maps to the point (0, -1), but this point on its own is a zero-dimensional subset, which we are allowed to ignore. Thus, a circle is birationally equivalent to ordinary 1-dimensional space, which means that it is a rational variety.
Some of the most exciting advances in algebraic geometry over the past few decades have been in better understanding the birational classification of higher-dimensional varieties. For example, Shigefumi Mori won the Fields Medal for his "Minimal Model Program", which attempts to find in each birational equivalence class a unique simplest variety. There have also been very important breakthroughs in characterising rational varieties: that is, in finding ways of telling whether a variety is rational.
Along with his work on birational classification, Kollár's most recent work stands out in a direction that will greatly affect algebraic geometry in the decades to come, as an important complement of the Minimal Model Program: the definition and study of moduli of higher-dimensional varieties, which can be thought of as sophisticated geometrical structures whose points represent equivalence classes of these varieties. The importance of this area can be seen in the immense wealth of papers on the moduli problem in dimension 1, which today occupies topologists, combinatorialists and, perhaps most of all, physicists. Already for surfaces the treatment of moduli is an extremely subtle and difficult problem. Kollár's ideas have almost defined the field of higher-dimensional moduli.
Among Voisin's major achievements is the solution of the Kodaira problem, which starts with the observation that every deformation of a complex projective manifold is a Kähler manifold (which roughly speaking means a geometric set that locally has a structure compatible with the complex numbers) and asks whether the converse is true. She found counterexamples: that is, Kähler manifolds that do not just fail to be deformations of projective manifolds but are not even topologically equivalent to projective manifolds. Another of Voisin's pioneering accomplishments is the establishment a new technique for showing that a variety is not rational, a breakthrough that has led to results that would previously have been unthinkable. A third remarkable result is a counterexample to an extension of the Hodge conjecture, one of the hardest problems in mathematics (it is one of the Clay Mathematical Institute's seven Millennium Problems), which rules out several approaches to the conjecture.
Algebraic geometry is a central area of mathematics that has seen many remarkable developments in its history, and these developments continue to the present day. In their different ways, János Kollár and Claire Voisin have made profound contributions to algebraic geometry that will deeply influence the future of the subject.
26 September 2017
Hong Kong
3.6. János Kollár autobiography.
I was born in 1956 in Budapest, Hungary, the oldest of six children in a close family full of engineers and musicians. I was a bookish child, interested mostly in history, adventure stories and the sciences. Around age eight I developed a strong stammer, which further led me to reading. The stammering gradually subsided over the next fifteen years, but hints of it remain with me, especially when I am tired of giving talks.
In elementary school I was an undistinguished student, getting middling grades in many classes but doing well in the few that interested me. Luckily my parents had confidence in me, and for high school sent me to the Piarist Fathers. Their school, called the Budapesti Piarista Gimnázium, was founded in 1717. During the communist years it was barely tolerated by the government, but it was probably the best school in Hungary. After getting many failing grades in the first weeks, I came to understand that I had to work hard, and by the end of the first year I was near the top of my class. This was really the experience that started me on the path toward knowledge and science. My two most influential teachers were János Pogány, who taught mathematics, and Zoltán Fórián-Szabó, who taught physics and chemistry.
It was also at this time that I got involved in mathematics competitions. These had a long tradition in Hungary; the first competition for high school students was established in 1894. Those who did well were invited to participate in a monthly meeting where we worked on developing our problem-solving skills. This was a great opportunity to meet other students who were also interested in mathematics, and spur each other on to do better. Each year the best of us were sent to the International Mathematical Olympiad. I was selected twice and returned with a gold medal both times.
After a year of mandatory military service, I enrolled in Eötvös Loránd University in Budapest as a mathematics student. Here I was mostly influenced in my first year by László Babai and later by Ervin Fried. They told me that there was this large branch of mathematics, called algebraic geometry, which was completely unknown in Hungary at that time. So I decided to learn it. For two years I worked completely alone, with only a few books. It was slow going, with nobody to consult, but it resulted in my learning the foundations very well. After that I spent two semesters in Moscow as an exchange student, where I attended the lectures of Iskovskikh and Manin, and the seminar of Shafarevich. At the end of university I applied to enter the PhD programme in Moscow. I had strong support from the Russian mathematicians, but, to my surprise, the examiner failed me on the required Marxism-Leninism exam. I was very disheartened, but this turned out to be one of the great lucky twists in my life.
I had met David Eisenbud when he visited Hungary during my undergraduate years, so when Moscow fell through I wrote to him, asking to be a student in the USA. This was somewhat illegal at that time, so my whole application consisted of that letter. He arranged for a full scholarship for me, and in 1981 I arrived at Brandeis University, where I studied with Teruhisa Matsusaka. He taught me to aim to be not only a technician but a scientist, maybe even a natural philosopher. It was also there that I met my wife, Jennifer Johnson.
I graduated in 1984 and started a Junior Fellowship at Harvard. The Fellowship gave me an opportunity to spend three months in Nagoya and begin my collaboration with Shigefumi Mori. This turned out to have a decisive influence on my work, both in our joint papers, books and in my work ever since.
In 1987 I accepted an invitation from Herb Clemens and joined the mathematics department at the University of Utah in Salt Lake City. The next twelve years were very fruitful, with several visits by Mori, Miyaoka, Voisin, and three intense Summer Seminars where dozens of young algebraic geometers came together to work on the rapidly developing minimal model programme, the moduli theory of canonical models and the early stages of the study of rationally connected varieties. These three topics have been the main areas of my research ever since. It is also in Salt Lake City that our daughter Alicia was born; she is currently a Postdoc at Princeton in experimental physics.
In 1999 we moved to Princeton University, where we have been ever since. Since then I have learned the most from my students, especially from ongoing collaborations with Alessio Corti, Sándor Kovács and Chenyang Xu. I hope to continue learning for many years to come.
26 September 2017
Hong Kong
3.7. Kollár receives 2017 Shaw Prize in mathematics.
János Kollár, the Donner Professor of Science and professor of mathematics at Princeton University, is a co-recipient of the 2017 Shaw Prize in mathematical sciences. Awarded by the Hong Kong-based Shaw Foundation, the Shaw Prize honours recent breakthroughs by researchers in the fields of mathematics, astronomy, and life science and medicine.
Kollár will share the $1.2 million prize with Claire Voisin, a professor and chair in algebraic geometry at the Collège de France. Kollár and Voisin were recognized for their "remarkable results in many central areas of algebraic geometry, which have transformed the field and led to the solution of long-standing problems that had appeared out of reach," according to the prize citation. The 2017 prizes will be awarded during a Sept. 26 ceremony in Hong Kong.
Kollár joined the Princeton faculty in 1999. Among his many honors, he became a member of the National Academy of Sciences in 2005 and an external member of the Hungarian Academy of Sciences in 1995. He received the Cole Prize in Algebra in 2006 and was named a Simons Fellow in Mathematics in 2012 and a fellow of the American Mathematical Society in 2013. He received his Ph.D. from Brandeis University and his B.S. from Eötvös L University in Hungary.
Media mogul and philanthropist Run Run Shaw founded the Shaw Prize in 2002. Other current Princeton faculty who have received the Shaw Prize include: Bonnie Bassler, the Squibb Professor in Molecular Biology and chair of the Department of Molecular Biology who received the 2015 Shaw Prize in life science and medicine; and Lyman Page, the Henry De Wolf Smyth Professor of Physics, and David Spergel, the Charles A Young Professor of Astronomy on the Class of 1897 Foundation, who received the 2010 Shaw Prize in astronomy. P James Peebles, the Albert Einstein Professor of Science, Emeritus, and professor of physics, emeritus, was awarded the 2004 Shaw Prize in astronomy.
3.8. János Kollár: Laureate Video
Diana Lin: The 2017 Shaw Prize in Mathematical Sciences is shared by two algebraic geometers whose amazing results in many key areas transformed their field and led to solutions to long standing problems that had seemed unreachable.
Chris Lincoln: When János Kollár flies into Kong Kong for the Shaw Prize ceremony he'll likely look up at the roof of the passenger terminal. He sees patterns of elliptical lines.
János Kollár: I worked on exactly understanding the type of surfaces that are made up of 2, 3 or more grids of ellipses.
Chris Lincoln: János has been in the mathematics department at Princeton University for 18 years. Before that he spent a dozen years at the University of Utah.
János Kollár: I'm especially interested in the cases where the shape is very sensitive to small changes of the numbers.
Chris Lincoln: Like the Lemniscate of Bernoulli.
János Kollár:
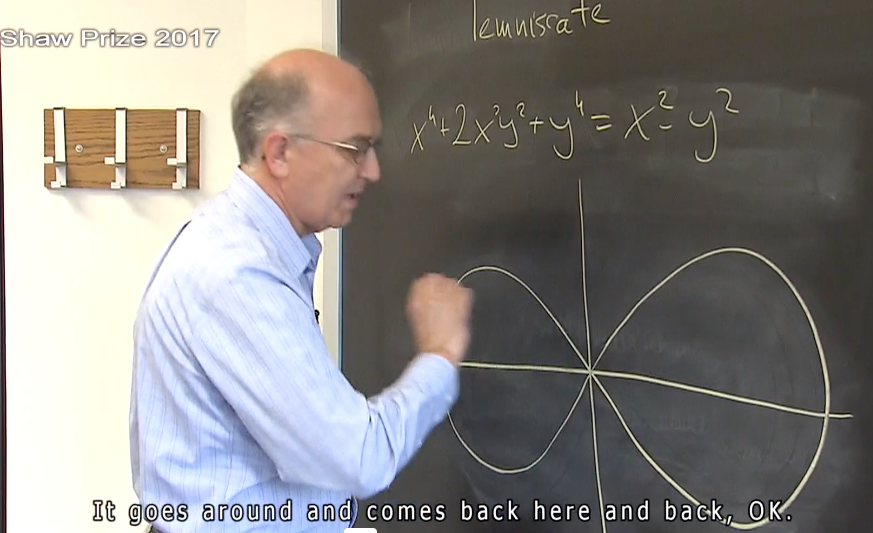
Consider
.
It looks like a nice figure of eight. It goes around and comes back here and back, OK.
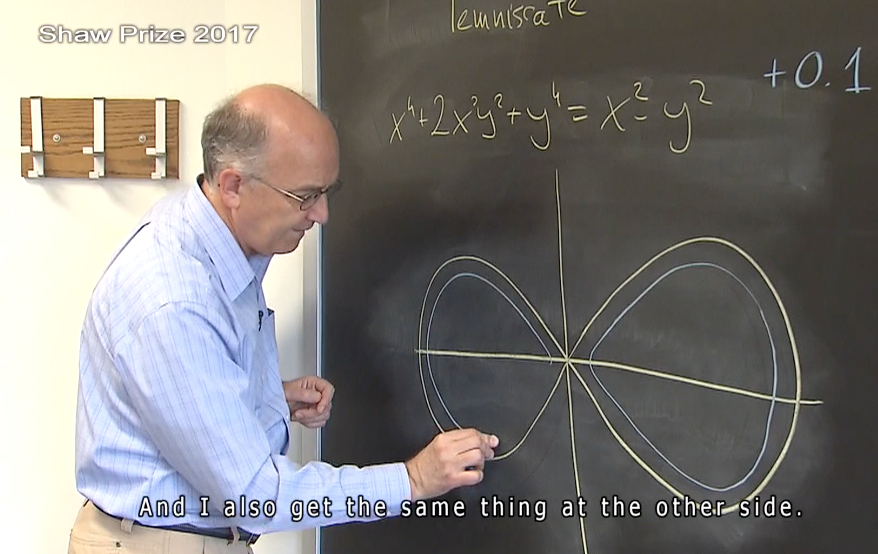
What happens if I add to it a plus zero point one?
Turns out I get something that hugs the figure eight from the inside. So I get something like this. And I also get the same thing at the other side.
Instead of being made out of just one piece of matter, its suddenly made out of two pieces.

Chris Lincoln: And the blue lines don't intersect.

János Kollár: What happens if I subtract zero point one from it?
Well then again I get something that will hug the figure 8 but this time it will hug it from the outside. It doesn't have this part where it intersects.
You can think of it as a circle where you're trying to bring the top and the bottom together.
Nicholas Katz: This idea of what he calls rationally connected varieties, which he wrote a whole book about, that was a brand new insight.
Richard Taylor: He disproved a very longstanding conjecture of John Nash, who both won a Nobel Prize in Economics and an Abel Prize.
Chris Lincoln: As a graduate student at Brandeis University, János met his future wife Jennifer, who is also now a mathematician at Princeton.
Jennifer Johnson: When he's working I can't think about anything else because it looks like something is going to explode over there and this can go on for quite a while.
János Kollár: I'm attacked by mathematics. Then for 3 weeks, I'm ill.
Chris Lincoln: János is the only member of his family in North America. He left his native Hungary after university. János is surrounded by engineers. That includes his brother Peter, his parents, and now his daughter, Alicia, an electrical engineer.
János Kollár: What I especially like is when I teach a class of non-mathematicians and then at the end of the year one or two students usually come to me and say "I would like to be a mathematician now."
4.1. The János Bolyai Award.
The Hungarian Academy of Sciences established the János Bolyai Award in 1902 in honour of the hundredth anniversary of the birth of the world-famous Hungarian mathematician János Bolyai to reward outstanding mathematical work. The awarding of the medal was discontinued after the outbreak of World War I; in 1994, the Hungarian Academy of Sciences re-established the award as the János Bolyai International Mathematics Award.
Every five years, the Bolyai award is given by the Hungarian Academy of Sciences to the author of the most outstanding and groundbreaking mathematical monograph of breakthrough significance, presenting new results and methods of the author's own, published anywhere and in any language in the previous fifteen years, taking into account the author's previous scientific work.
One year before the presenting of the award, the Department of Mathematical Sciences of the Hungarian Academy of Sciences elects a committee of five full members and five prominent foreign mathematicians and appoints its chairman. The committee reports its decision to the President of the Department no later than three months before the award is given. The Committee elects its own representative from among its members, who presents a detailed presentation of the work of the laureate at the award ceremony and prepares a written report. The chairman also votes in the committee and, in the event of a tie, casts the deciding vote.
The award includes a prize of US$25,000 and a gold-plated bronze medal made using the original designs.
4.2. The 2025 János Bolyai International Mathematics Award.
This prestigious award is given every five years by the Hungarian Academy of Sciences to the author of the most outstanding and groundbreaking mathematical monograph of breakthrough significance, presenting new results and methods of the author's own, published anywhere and in any language in the previous fifteen years, taking into account the author's previous scientific work. According to the committee responsible for the award, János Kollár's achievements have had an invaluable impact on modern complex algebraic geometry.
4.3. Essay on the 2025 János Bolyai Award.
The award committee, comprising five full members of the Department of Mathematical Sciences of the Hungarian Academy of Sciences and five prominent foreign mathematicians, determined that while almost all areas of pure mathematics involve classification problems, a special feature of algebraic geometry is that it does not consider classification problems as completed once the objects in question are classified as elements of a set. Rather, it is interested in giving these classifying sets a geometric structure; this idea leads to what is called modular theory, where objects are classified by constructing moduli spaces, which can be used to parameterise the objects.
A classic example is the construction of a moduli space of smooth curves of at least two genus. Its construction was the crowning achievement of a hundred years of work that began with Riemann and ended with the work of Deligne, Grothendieck and Mumford. Mumford introduced geometric invariant theory (GIT) as a way to construct moduli spaces which can be expressed as the quotient of a variety by a reductive algebraic group. The end product is the moduli space of stable curves, which is a geometrically meaningful compactification of the moduli space of smooth curves. Gieseker made the first progress in the analogous higher dimensional case with a moduli space of surfaces of general type in 1977.
Unfortunately, no one has been able to apply the techniques of GIT beyond the case of curves. The 1988 publication of Kollár and N Shepherd Barron, Threefolds and deformations of surface singularities, marked a breakthrough in the theory of moduli. Instead of GIT, this paper proposed to use ideas from birational geometry. The paper was the beginning of a monumental effort, including more than thirty major papers by Kollár, culminating in his book Families of varieties of general type.
The part of the programme dealing with surfaces was completed in the early 1990s. The construction of the moduli space in all dimensions required considerably more work. Kollár has always been the main driving force behind this programme, and he has contributed the lion's share of understanding the overall picture in this regard.
It is impossible to understate how influential this general research programme has been in modern complex algebraic geometry. The solution to this problem not only originated with Kollár (and Barron), but substantially more than anyone else, has been developed by Kollár over his entire career. Almost every aspect of its construction has been deeply influenced by, or solved by, Kollár.
One important aspect of Kollár's theory is its wide-ranging applicability. What Kollár achieves through this book is fundamental, across all moduli theories of varieties. As is true of all his books, Families of varieties of general type, although presenting the reader with some very serious technical challenges and being full of profound insights, has a clear structure, clear explanations and provides detailed exposition of the motivation of the concepts, making it an enjoyable read and an attractive way to study the moduli of varieties of general type; it is required reading for anyone working in the moduli theory of varieties. This book is written by the master of the field - it is a crowning achievement in algebraic geometry.
The Hungarian Academy of Sciences established the János Bolyai Award in 1902 in honour of the hundredth anniversary of the birth of the world-famous Hungarian mathematician János Bolyai to reward outstanding mathematical work. The awarding of the medal was discontinued after the outbreak of World War I; in 1994, the Hungarian Academy of Sciences re-established the award as the János Bolyai International Mathematics Award.
Every five years, the Bolyai award is given by the Hungarian Academy of Sciences to the author of the most outstanding and groundbreaking mathematical monograph of breakthrough significance, presenting new results and methods of the author's own, published anywhere and in any language in the previous fifteen years, taking into account the author's previous scientific work.
One year before the presenting of the award, the Department of Mathematical Sciences of the Hungarian Academy of Sciences elects a committee of five full members and five prominent foreign mathematicians and appoints its chairman. The committee reports its decision to the President of the Department no later than three months before the award is given. The Committee elects its own representative from among its members, who presents a detailed presentation of the work of the laureate at the award ceremony and prepares a written report. The chairman also votes in the committee and, in the event of a tie, casts the deciding vote.
The award includes a prize of US$25,000 and a gold-plated bronze medal made using the original designs.
4.2. The 2025 János Bolyai International Mathematics Award.
This prestigious award is given every five years by the Hungarian Academy of Sciences to the author of the most outstanding and groundbreaking mathematical monograph of breakthrough significance, presenting new results and methods of the author's own, published anywhere and in any language in the previous fifteen years, taking into account the author's previous scientific work. According to the committee responsible for the award, János Kollár's achievements have had an invaluable impact on modern complex algebraic geometry.
4.3. Essay on the 2025 János Bolyai Award.
The award committee, comprising five full members of the Department of Mathematical Sciences of the Hungarian Academy of Sciences and five prominent foreign mathematicians, determined that while almost all areas of pure mathematics involve classification problems, a special feature of algebraic geometry is that it does not consider classification problems as completed once the objects in question are classified as elements of a set. Rather, it is interested in giving these classifying sets a geometric structure; this idea leads to what is called modular theory, where objects are classified by constructing moduli spaces, which can be used to parameterise the objects.
A classic example is the construction of a moduli space of smooth curves of at least two genus. Its construction was the crowning achievement of a hundred years of work that began with Riemann and ended with the work of Deligne, Grothendieck and Mumford. Mumford introduced geometric invariant theory (GIT) as a way to construct moduli spaces which can be expressed as the quotient of a variety by a reductive algebraic group. The end product is the moduli space of stable curves, which is a geometrically meaningful compactification of the moduli space of smooth curves. Gieseker made the first progress in the analogous higher dimensional case with a moduli space of surfaces of general type in 1977.
Unfortunately, no one has been able to apply the techniques of GIT beyond the case of curves. The 1988 publication of Kollár and N Shepherd Barron, Threefolds and deformations of surface singularities, marked a breakthrough in the theory of moduli. Instead of GIT, this paper proposed to use ideas from birational geometry. The paper was the beginning of a monumental effort, including more than thirty major papers by Kollár, culminating in his book Families of varieties of general type.
The part of the programme dealing with surfaces was completed in the early 1990s. The construction of the moduli space in all dimensions required considerably more work. Kollár has always been the main driving force behind this programme, and he has contributed the lion's share of understanding the overall picture in this regard.
It is impossible to understate how influential this general research programme has been in modern complex algebraic geometry. The solution to this problem not only originated with Kollár (and Barron), but substantially more than anyone else, has been developed by Kollár over his entire career. Almost every aspect of its construction has been deeply influenced by, or solved by, Kollár.
One important aspect of Kollár's theory is its wide-ranging applicability. What Kollár achieves through this book is fundamental, across all moduli theories of varieties. As is true of all his books, Families of varieties of general type, although presenting the reader with some very serious technical challenges and being full of profound insights, has a clear structure, clear explanations and provides detailed exposition of the motivation of the concepts, making it an enjoyable read and an attractive way to study the moduli of varieties of general type; it is required reading for anyone working in the moduli theory of varieties. This book is written by the master of the field - it is a crowning achievement in algebraic geometry.
Last Updated September 2025