I am generally a pessimist. If I look at life and see that on one scale pan you can put all our suffering, all our disappointments, what we failed at in life, what "didn't work out" for us, as they say in everyday language, and on the other scale pan you can put moments of happiness, moments of contentment, satisfaction - it seems to me that this black scale pan is heavier, that it outweighs everything. But you can overcome all this if you have some passion, some love. Then even these dark moments in life become possible to survive. So I have to say that in my life, in my childhood and my youth, such a big role was played by two great passions that I had. Namely - this is very funny to say to students today - one of my passions was school, and the other was the mountains.

I went to school in Zakopane until I graduated from high school. School was the centre of life, not like it is now. Of course, this is understandable: there was no radio, no television, life revolved around school. School taught us to read, to read not only with understanding, but with a great sense of beauty in literature. And this humanistic education is very necessary for me, as a mathematician and mathematics educator; especially as someone who deals with mathematics education, because it gives insight into the human soul. First of all, when I was still a student at school, I read a lot of books; everything that could be got hold of, we read, and not only in one language. Namely, we had French, German, and Latin: three languages, each with a rich literature. Above all, we could read in these languages. Among other things, we read Goethe's "Faust" in German, which is connected with an amusing anecdote.

Two years ago, during the Mathematical Congress, I was sitting on a bench in the park with a Dutchman and a German, namely Professor Freudenthal, a great friend of mine, and Professor Steiner from Bielefeld. The conversation turned to my dog ​​and unfortunately I couldn't remember what this breed of dog is called in German. (Very funny, because it's called the same in Polish, but I didn't remember it at the time.) I kept repeating in French caniche, caniche and - finally I had a brilliant idea: I said to Professor Steiner, "You know, this is the same breed as that dog in one of the first scenes of 'Faust'." And Steiner exclaims: poodle.

It was the same with Latin, for example. In our class there was a group of girls (the class was coeducational) who had ambitions to translate Latin poems into Polish with rhythm and rhyme: Ovid's "Metamorphoses" and various others. So I also had an excellent Latin teacher, who wonderfully introduced us to Roman culture, which at the same time was able to combine with the Zakopane landscape. For example, during a lesson, when the snow-covered Giewont could be seen from the windows of our classroom, we were working on a poem by Horace. The professor stopped and said: "Vides ut alta stet nive candidum Soracte"- you see how Soracte sticks out, white with snow. This school was a real school of humanism. At that time, mathematics was a subject I liked very much at school, and I really felt very good at it. Apart from that, it was the basis of my existence, because I could give lessons. But I received a humanistic education, a passion for reading, the ability to read in a foreign language. I know that, for example, while I was studying in Kraków, at the University of Kraków, I read, for example, Thomas Mann: "Zauberberg", "The Magic Mountain", in German, even though it is certainly quite difficult reading in German, and the translation was later; so that was the first time I encountered Thomas Mann in the original version. I learned all of this from school, only from school; I never had any private lessons or conversations, because I couldn't afford them. My family conditions were terrible: it was poverty, there were five people in one room and in terrible conditions; I spent whole afternoons giving private lessons; I was very poorly dressed, I never had good shoes, I never had a decent coat. But above all of that was this passion.

The second passion is the mountains. And again today, when it comes to sports, we have an incredible number of articles, that this is missing, that is missing, the equipment is not the right skis, the wrong boots, etc. And I had no equipment, terrible shoes, some awful trousers pulled out from somewhere, somehow darned, embroidered - and wonderful experiences in the mountains; wonderful! It is unforgettable! Anyone who has not spent a night in the mountains under the open sky cannot understand what it means that silence is full of sounds, mountain silence, which is not there, because something is constantly dripping, something is constantly rustling, something is constantly blowing, knocking, a stone is flying, water is pouring... It is something that is indescribable, incommunicable. And an extraordinary passion to go there only to survive, to be able to take a relaxation from this everyday work, precisely in - as they say very pathetically - the bosom of nature; but this does not convey what it was. I had a friend who had just killed herself in the mountains and who had been hiking with me since I was a student: Jagienka Honowska, a famous mountaineer. We hiked in such difficult conditions (she didn't have much money either) and very often spent the nights outdoors; not because we wanted to, but because we didn't have money for a shelter. We had this machine, a bag of semolina, some bread and we were happy that we could: that we could go to these mountains, that we had this strength, that we could still survive. It was a great happiness, despite all the hardship and the fact that it took place in such conditions.

When I had to choose my studies, I could choose the humanities; what's more, I was promised a scholarship by the Ministry if I went in that direction, if I went to literature. Unfortunately, my love of mathematics won out and I went to mathematics, to the Jagiellonian University. Here again, stimulated by this wonderful University and excellent professors, I developed a passion for science. We were really dazzled by our studies in our first year, despite the difficulties. There were a hundred of us in our first year, and twenty in our second, and the requirements were enormous. And indeed, only those who had this passion, had a love, could pass these requirements. Without a student house, absolutely without any scholarship, supporting myself solely with lessons, from the very beginning with these lessons, in addition to which I also had to help my mother and younger siblings. As a result, I studied for a long time, because I had to spread out my studies; I could not do it at the same pace as my colleagues who had good conditions. I had only one help: they saved me tuition fees. The university was paid, not for free! The war "saved" me from paying the tuition fees, which I had been paying to the Jagiellonian University until 1939. When the war broke out, all these debts were already put on the line. Fortunately, they have not mentioned it since then. Maybe I paid off the tuition fees later with my own work, because I also gave lectures at the University, or maybe out of gratitude to the University itself, which was also able to awaken new passions.

Professor Witold Wilkosz was here, to whom we owe a great deal in this respect, that he awakened in us a passion for teaching mathematics, for finding means of good teaching, for involving people in mathematical thinking. He was somehow able to convey this to us, even though he was a man of great imagination; he was also a great humanist, he knew music wonderfully, painting wonderfully, literature. And he was also a mathematician and somehow everything worked well together.

Of course, there are narrow-minded people among mathematicians, who do not see anything outside their field. But among mathematicians there are many people who are extremely attracted to music, who know music, who like music. Apart from that, there are many people with humanistic passions.

I chose mathematics, studied in incredibly difficult conditions, about which today students have no idea. When I was the dean at the Higher School of Pedagogy, we had very difficult housing conditions for young people and sometimes these young people came to me with some complaints. And I said: not with me, my dears, don't come to me with such complaints, I am completely insensitive to it! They always laughed that I was so insensitive to their misery, to their complaints. And today, young people have much better conditions.

University was a very hot period of life from the point of view of such a passion directed towards science. And at the same time, there were these mountains, constant trips to these mountains, even climbing. I had a very serious accident, which interrupted my studies for a year. I fell from the Kościelec Ridge. The rope broke, I fell, I flew far away, then I was ill for a whole year after the accident. But that did not stop me from continuing these trips. When I went to Fajki for the first time with two friends, I told them: listen, I don't know if I will not have some kind of hysterical attack on these Fajki. But no, absolutely nothing, this great passion remained.

Then came the war and of course the secret education. Wonderful young people who studied, although they didn't have to. Finally, such a meeting with such young people! I not only taught, but I was a courier for the secret school authorities. During one of these business trips to the Vilia River, the Germans locked us up in Tarnów at the station for the whole night, in such a small room, terribly crushed. At that time, the war with Russia was already underway, the Germans were returning for the holidays from the Eastern Front, swarming with lice; and apparently one of these lice bit me, so that I fell seriously ill with typhus. Later, I was offered such a position in an enterprise, which consisted of many sawmills scattered around the Gorce Mountains, Ochotnica, Tylmanowa, Krościenko. I was to work as an accountant, and at the same time I was to conduct secret education, because the director of secret education in Podhale had to flee (they arrested his wife and wanted to arrest him as well). The school authorities simply sent me there in that role, and I was officially registered as an accountant in that enterprise. And here again the mountains were associated with my activity, because I was obliged to travel or walk all over Podhale to inspect the secret education centres in Rabka, Zakopane, Maków, Jordanów, Ochotnica Wielka near Turbacz. This job made it easier for me, because these were sawmills, so I went to inspect sawmills. I knew a lot about wood! I don't remember now, but at that time I knew all those boards, those measuring sticks, those long logs so well... So I went to the sawmill and at the same time I inspected schools, organised final exams, exams. All of this had to be well supervised.

I was actually scared. I can't say I was brave in the sense that some people who were brave at that time. I was very afraid. It was a nightmare, I even dreamed about it at night. I must say that I was very afraid. But like Kali in Sienkiewicz's book, "Kali was afraid, but you had to go". There was no other way. Besides, this contact with the youth, with the teachers, is such an incredible elevation of human dignity when this dignity was so humiliated. Some great pride, a sense of humanity when this humanity was simply being trampled. I remember, exactly once, I was travelling from Kraków to Nowy Targ, because then I lived in Nowy Targ until the end of the occupation. At that time I was carrying this whole big suitcase of school textbooks, and at the same time a whole lot of highlanders were traveling, who were carrying bread from Miechowski; because there was no bread in Podhale. Of course, the train was darkened, so there was no light, because everything was darkened. Just a bunch of people, people leaning on each other; a terrible crowd of people standing. And that smell of bread, which I remember to this day! Such fresh bread! They were taking these loaves to Podhale from Miechowskie, near Kielce. This smell of bread, and at the same time these books ... Some deep reflection - bread and books ...

My passions did not fade. Despite the difficult conditions in every respect, primarily material, but also other aspects were very difficult, I always came across some kind of bonfire, by which I could warm myself, by which I could stretch and start doing something again. I was lucky to come into contact with such people, who also raised these passions in me, were able to sustain them. And then I moved to the Higher School of Pedagogy and again this school gave me the opportunity to develop a new passion: to raise didactic research to a scientific level and create a kind of new discipline in Poland. In 1956 I went on a delegation to Geneva for the Conference of the International Bureau of Education UNESCO and there I already forged such bonds of almost friendship with various people in the West. So then I had a lot of contacts in the East and the West and again I was lucky enough to have a group of people who somehow had similar passions.

I'm going back to the starting point: life is very difficult and it cannot be denied that we have a lot of adversities, a lot of difficulties, a lot of misfortunes, sometimes personal, national and various complications. And I think it would not be possible to survive if a person was not passionate about something, did not really love something, did not really devote themselves to something with some conviction that it is worth doing, that it must be done. When I look back, of course I look critically at various achievements. It seems to me that it was not good, certain problems could have been solved differently, whether personal matters or in my work. But I think that these passions, constantly occurring, increasingly different, helped me a lot.

If I had to live my life over again, I would live it in my thinking, in my feeling, in my experiencing the same way. Certainly nothing has changed in relation to literature, in relation to music. When I listen to Mozart, it sometimes seems to me as if I were in some stream of pure cold water. I am not a musician, I do not know anything about it from a professional perspective. However, I can experience it very strongly. And, it is true, then these mountains, these friends in the world - all of this has some enormous value ...

The reform of the mathematical studies of future teachers has been proposed for a long time. The new trends in mathematical education have highlighted the particular urgency of this reform, because the difficulties in modernising elementary mathematics arise not only from the outdated mathematical knowledge of many older teachers, but also from the methodological indolence of many other teachers who have received modern mathematical education. We also note the defects of the too rapid and too formal recycling of teachers in service, which leads in some teachers to the fascination with modern mathematical terminology often covering the lack of a deeper mathematical culture.

This is why the international symposium devoted to the problems of teaching mathematics in secondary and higher schools in European countries, which took place in Bucharest in 1968, stressed the urgency of work concerning:

1. the analysis of the current structures of scientific studies of future teachers from the point of view of their effectiveness for the exercise of the profession of mathematics teacher;
   
   
2. the improvement of these structures as and when needed;
   
   
3. their adaptation to the real level of recruitment of future mathematics teachers.

The discussion concerning all these problems should be based on the answers to the following three questions:

1. What are the general objectives of mathematical education at the school level currently envisaged and in the perspective of the development of science, technology and social structures?
   
   
2. What knowledge and intellectual and cultural attitudes of teachers could guarantee the achievement of the goals thus defined?
   
   
3. What are the real conditions for training mathematics teachers in the given society: recruitment to the profession, qualifications of the managers training future mathematics teachers, etc.?

Many international and local congresses have dealt with these questions. Their conclusions most often express the same postulates. The Bucharest conference -previously mentioned - expressed some of these general ideas as follows: "the social objective of education is twofold:

1. To transmit mathematical culture to society and to develop the mathematical potential of each individual as best as possible.
   
   
2. To train specialists who will teach mathematics, advance fundamental and applied research, develop applications in collaboration with specialists in the disciplines concerned ...

"The attention paid to secondary education must not be restricted to the orientations that lead to higher education. The other orientations of secondary education deserve more attention than they have received so far" [1]. The idea of ​​"mathematical culture for all" was reinforced in the conclusions and recommendations of the First International Congress on Mathematical Education held in Lyon in 1969, which recommended to the CIEM [(International Centre for Mathematical Meetings]: "With regard to the structure of the next congress, give more attention to pre-school education, elementary education, mathematical education for all young people, and adult education" [2]. The Lausanne conference on the coordination of mathematics and physics teaching accepted as a principle for work on the modernisation of elementary mathematics: "every child has the right to be introduced to the world of elementary and fundamental structures of mathematics" [3].

The problems of the mathematical studies of future teachers are therefore not reduced to the problems of training an elite of teachers for an elite of students. On the contrary, our very important and very difficult task is the modern training of the mass of teachers for the mass of students, because it is not through the elite of teachers and the elite of students that we could raise the level of mathematical culture of the whole society.

In the course of many international meetings the very concept of this "mathematical culture for all" has been analysed, highlighting the following features:

1. basic knowledge structured with the help of mathematical structures considered fundamental at the given stage of the development of science;
   
   
2. awareness - even if only approximate - of the formal construction of mathematics, its relationship with reality, its multilateral relations with other sciences: fundamental concepts of the scientific methodology of mathematics, definition, theorem, demonstration, mathematisation, axiomatic method, interpretation and application of mathematical theory, etc.;
   
   
3. initiation to the various processes of mathematical thought in action: abstracting, schematising, mathematising, deducing, searching for and discovering mathematical connections, generalising and specialising, using mathematical symbolism, concrete and thought models in solving problems, rationally organising the data of the problem, etc.;
   
   
4. ability to correctly express one's own mathematical thought: defining, clearly presenting the reasoning, formulating the problem in a precise manner, etc.:
   
   
5. a certain technique of individual study in mathematics: knowing how to read mathematical texts efficiently, checking the results of individual work, looking for and correcting mistakes made during this work, etc.

Obviously, the concrete interpretation of this concept of "general mathematical culture" should be balanced in terms of the content of knowledge and the level of abstraction, taking into account the possibilities of the students and the conditions of education. But this restriction will not change the essence of this concept: the mathematical culture of society is not only the skill in simple arithmetic calculations and the knowledge of certain geometric concepts and theorems, but above all the understanding of the mathematical method of thinking, of solving problems, the understanding of the relational and structural character of contemporary mathematics and the awareness that it is precisely thanks to this abstract and relational character that mathematics has become omnipresent in our civilisation today.

The transmission of this awareness to the broad strata of society is one of the most important objectives of the modernisation of elementary mathematics and one of the primary objectives of general education.

This objective entails the inevitable implications concerning the adequate training of teachers of mathematics:

1. The mass of teachers must be prepared for the mass of students.
   
   
2. It is therefore not possible to restrict recruitment to the profession of teaching mathematics to very gifted students. On the contrary, one must count above all on average students, and in some countries even weaker ones, as representative candidates for this profession.
   
   
3. These average or even weaker students must be introduced, during their studies, to the contemporary mathematical world quite deeply, not only from the point of view of the extent of their knowledge, but also from the point of view of their general mathematical culture, in the sense previously defined.

The current structure of mathematical studies of future teachers is not adapted to these social conditions and social needs. For many average students their mathematical studies are only permanent and forced preparation for exams that deal with isolated topics, a preparation that neglects the structure of the subject, that does not know any methodological reflection, but is primarily focused on memorising the content presented by lectures and on assimilating certain mechanisms in solving typical problems. Such a study, based on forced information and not on the formation of the mathematical mind, is not favourable to the active assimilation of mathematical culture by future teachers of mathematics.

The future researcher also goes through this period of forced information. But (1) he is more gifted, so he prepares more easily and more quickly for exams, so he has time to study basic mathematics more actively, he has time to think; (2) he develops his mathematical activity in the rest of his studies, during advanced seminars, during research. It is by doing mathematics that he actively assimilates the mathematical culture of his time. The studies of a student, a future teacher, most often stop at this stage of basic information. It therefore happens too often that the teacher of mathematics is obliged to actively introduce his students to the rudiments of a mathematical culture, to which he himself has not been initiated more deeply.

This state of affairs could not be effectively improved without changing the current conception of the mathematical studies of future teachers. The analysis of this conception made during the fervent discussions in some countries - e.g. in Poland - leads to the following conclusions:

1. The initial mathematical training of students who are oriented towards teaching requires a specialisation aimed expressly at the needs of their future profession.
   
   
2. Overloaded curricula hinder the mathematical activity of average or weaker students, who are representative of the mass of future teachers. Experience proves that certain reductions in content, the elimination of details in favour of the in-depth treatment of ideas and techniques that are particularly important from the point of view of the modern mathematical spirit and its transmission at the elementary level, prove favourable to the development of the mathematical activity of these students.
   
   
3. The presentation of mathematics should be based on a synthetic conception of this science. Instead of studying many loosely connected subjects, instead of being forced to pass a large number of detailed examinations, the student - the future teacher - should be introduced to the mathematical world by few paths leading him quickly and directly to the essential.
   
   
4. The mathematical training of a good teacher requires his initiation into individual study and genuine mathematical research, adapted nevertheless to his rather modest possibilities. This postulate would not be realised without reducing the time devoted to lectures in favour of seminars and consultations, without a new conception of supervised work. The traditional exercises concerning the almost mechanical application of the theory presented by the lecturer to the solution of standard problems should be supplemented and partially replaced by placing students in open mathematical situations leading to thought processes such as: generalising a notion or a theorem, identifying a new notion during the process of mathematisation, constructing examples and counterexamples, formulating problems and hypotheses, etc. It should not be forgotten that analogous situations form the basis of modern mathematical teaching at school level. The teacher will not be fit for such teaching without analogous personal experiences gained during his studies under the direction of creative mathematicians.
   
   
5. From the point of view of the average student, many traditional lectures are nothing more than formal chains of definitions, theorems, and demonstrations. Behind this formal showcase, he does not see a living mathematics, with its past and perspectives, with the mechanisms of its development. Often, he does not know any motivation for this or that generalisation, and it happens too often that he does not see any connection between abstract theories and their simplest, most elementary models. He does not understand the intuitive meaning and scope of this or that method, etc. Many traditional lectures neglect methodological and historical commentaries that would highlight mathematical thought in action, which is particularly important from the point of view of the mathematical education of the future teacher. The reform of teachers' mathematical studies therefore requires a new conception of the lecture course.
   
   
6. The methodology of teaching mathematics has already passed the stage of practical apprenticeship of the profession and is increasingly becoming the field of research closely linked to mathematics and scientific methodology. The training of specialists in teaching cannot ignore this emerging discipline. During his studies, the future teacher should be introduced to the work carried out by the representative centres of methodological research in the same way that the future researcher becomes acquainted with the work carried out by the representative centres of his own specialty. The equipment of the Faculty should therefore ensure the sources of such information: methodological works, journals devoted to the problems of teaching, textbooks used in different countries, programmes of mathematical teaching in different countries, reports of the work done during the congresses on the problems of mathematical teaching, modern didactic materials, etc. The teacher who knows only one programme, only one conception of mathematical teaching, who is not interested in the experiments organised in other countries, who has not been introduced to the comparative study of the various conceptions of the modernisation of elementary mathematics, will very easily become hostile to new reforms in his own country. The formation of his flexible methodological spirit, open to research, resistant to the dangers of routine is one of the most important objectives of his scientific training.

The creation of certain institutions such as, for example, the chairs of the methodology of mathematical teaching within the Faculties or the Institutes of research on mathematical teaching so closely linked to the Faculties, proves that the reform of the training of teachers of mathematics has made certain progress.

Introduction

The extension of the period of compulsory school education poses to the organisers of education, educators, teachers and academics interested in the teaching of subjects related to their own discipline the difficult task of developing a concept of democratisation of education in the scope of individual school subjects within the concept of general universal education. The work I am presenting is an attempt to review the development of views on what "elementary mathematics for all" should be over the last twenty-five years. Due to the difficulties of accessing many materials and the diversity of trends and local situations, this review is necessarily both incomplete and superficial. I limit it to only some selected facts, which, in my opinion, shed light on the whole problem. I am primarily interested in the school reality, reflected in the curricula, the didactic goals and guidelines attached to the programme texts, and the discussion on the situation in mathematics teaching, the statements of various groups, both professional mathematicians and practicing teachers. Given the variety and breadth of this material, I am only concerned with what is actually happening in school, and I am not analysing purely theoretical concepts that have not been realised in this area. I am only touching upon those philosophical and methodological problems concerning the mathematical foundations and meaning of universal mathematical education, which are particularly exposed in the discussion on teaching mathematics. Against this background, I am treating Polish issues very briefly, considering them only in relation to certain concepts of "elementary mathematics for all" distinguished as model ones.

§1. Democratization of general education and school social selection

The tendency towards the democratisation of school general education is observed everywhere, although its implementation takes place in different forms and at different paces in different countries. In the simplest terms, it means making available to every young person a school, completion of which will ensure that he or she will obtain such an education. The thing is, however, how one interprets and implements this "access to general education" and how one understands the concept of general education. Access to school can be understood formally: Every child has the right to complete such a school, regardless of its social origin, race and nationality (in multinational countries), gender, social status, etc. A stronger interpretation can be accepted, expressed in the so-called "school obligation": Every normal child is obliged, within certain age limits, to attend such a school. And thus understood, the "school obligation" may be actually implemented or, on the contrary, remain within the sphere of a statute that is not fully enforced or even impossible to fully implement. Finally, as is the case even in developed countries, the "school obligation" is formally fully enforced, but attending a general secondary school of a given level and even receiving an appropriate document confirming its completion is not at all equivalent to the actual achievement of education in the general sense of the theoretical concept of this education.

The period of general compulsory education varies greatly in different countries. In many countries, the school obligation established by its very nature, even for a minimum period of 5-6 years, is subject to executive orders - often necessary - which are largely limited a priori due to local conditions. It is also often not implemented despite the legal basis there, where school constitutes an alien element - often treated as hostile - to social and family structures and traditions, or where the economic status of large masses decides on the necessity of involving children in the work of adults in order to survive. In vast areas of our globe, the lack of adequately prepared teachers, the lack of having their own textbooks adapted to local needs and conditions, the difficulties of the nature of language and many other reasons determine that the "school obligation" - although it exists in theory - is not implemented, which is often related to the not-so-distant colonial past of many developing countries.
...

§2. The selective role of mathematics as a subject of teaching

The modernisation of mathematics teaching in primary and secondary schools was associated with great hopes in the years 1960-1970, including the hope of realising the idea of ​​democratisation of mathematical education. It was believed that in the scope of school mathematics in its modernised concept, the content and language would be new for children in various situations due to their social status. It was argued that if differences in the everyday language used in a given environment significantly influenced a child's start in school education in humanities, then they should have no significance in teaching the new language that modern mathematics in school was to be. Much short wet experiments in France, however, were struck by the fact that children from intellectually more advanced environments, who had early contact with everyday language, in which there were many abstract terms, were more likely to overcome difficulties in mastering mathematics, in which, in modernised teaching, terminology, precision of language, and symbolism played such a large role. The difference was again determined by differences in the preschool experiences - including linguistic ones - of children of different classes, and to a large extent also by the actual environmental and economic conditions (conditions for the child's homework, educational support, tutoring).

These observations have been used in an aggressive critique of the privileged position of mathematics in general education; some left-wing circles, especially the extreme left in France, see mathematics as a school subject as an instrument of particularly effective social selection within a capitalist society, aimed at the constant internal reproduction of the ruling classes.
...

§3. Critique of scientism and "imperialism" of mathematics in science and teaching

The outstanding French mathematician Alexander Grothendieck, laureate of the Fields Medal, formulates the credo of scientism in the form of the following six myths:

Myth 1: Only knowledge produced by the exact sciences is true and real knowledge, which means that only that which can be expressed quantitatively or can be formalised or repeated any number of times under the same conditions in the laboratory, can be the content of true knowledge.

Myth 2: Everything that can be expressed in quantitative terms, or can be repeated under laboratory conditions, is an object of exact scientific knowledge and is therefore essential and deserves recognition.

Myth 3: The dream of science: a "mechanistic" or "formalist" or "analytical" conception of nature. All reality, including human experiences and relationships, social and political events and forces, can be expressed in the language of mathematics, in terms of systems of elements, and will be finally so expressed when science makes sufficient progress. In the limit, the world is only a particular structure within mathematics.

Myth 4: The role of the expert: knowledge, both through its development and through its transmission and teaching, should be divided into numerous layers or specialties: first into broad fields such as mathematics, physics, chemistry, biology, sociology, psychology, etc., which have been changed voluntarily as science progresses. In every case, knowledge about a given field is only worth the opinions of experts in that particular field; when the matter concerns more than one field, there is only the collective opinion of experts in those fields.

Myth 5: Only science and technology based on it can solve human problems.

Myth 6: Only experts are qualified to participate in decisions, because only experts "know",

Grothendieck further states that these myths, which are close to the Pythagorean idea: "Everything is number", introduce huge simplifications into the understanding of the variable complexity of natural phenomena and human experience. He admits that these themes, like any other, contain a blade of truth. Over the centuries, the supremacy of reason and intellect over other aspects of human experience, sensory, emotional, and ethical, has become established. And what is even worse, according to Grothendieck, in the course of recent centuries the imperialism of the experimental and deductive scientific method has gradually become established, identifying it alone with reason, and rejecting all others as "irrational", "emotional", "instinctive", "inhuman", etc.

Grothendieck believes that all these myths are errors. By strengthening the power of experts, it limits them spiritually and mentally, moving them away from the reality of living beings towards the mechanisms of cybernetics; it paralyses their moral commitment and personal responsibility in all areas of functioning of society as a whole, requiring constant crossing of paths between the three poles: thought, feeling, action. Scientism not only justifies the rigid hierarchy of society that already exists, but it strengthens it even more, pushing to its peaks also a hierarchical technocracy that decides the way of being of humanity for thousands of years ahead. Scientism has become the dominant ideology throughout the world. The ecological crisis is only one of many consequences of this ideology, one of the first manifestations of the enormous crisis of our civilisation. Scientism as an ideology is not only unable to overcome this crisis which it has itself caused, but is not even aware of it, because becoming aware of it undermines the scientism ideology in its essence.
...

§4. Contemporary Mathematics in the Opinion of Mathematicians

Emma Castelnuovo, in the quoted fragment of her didactic credo, calls for teaching "true mathematics". The "false mathematics" she criticises is mathematics that exposes all formal elements. However, only those who create it can decide what "true mathematics" is. In their opinions we should look for, at least in part, the answer to what kind of mathematics should be taught and is worth learning. Professional mathematicians largely agree on what should be counted as products of mathematics as a science, but they do not agree on the directions in which mathematics should be developed, they express different assessments of the effects of mathematical activity and the variety of ways in which they interpret such concepts as "mathematical method", "mathematical intuition", etc. Finally, they also often differ essentially in the philosophical interpretation of the world of mathematical abstraction and its relation to material reality. Now, for the problems of teaching mathematics, these views are of fundamental importance. To popularise mathematics, but what kind of mathematics? What is essential in this science, important for its understanding, worth including as a final element in the general culture of the society? It is not just about the selection of content, that is the least important thing, but something more important, about understanding what the "mathematical method" is, which we consider to play such a large role in our scientific times and technological revolution, in which the specificity of mathematical thinking, the mathematical act of creation is expressed.

Hans Freudenthal contrasts "ready-made mathematics" with mathematics as a specific activity. "Every mathematician knows subconsciously that, alongside ready-made mathematics, there is also mathematics as an activity, but it seems that few people know it consciously, and since it is rarely emphasised, mathematicians do not know it at all." The answer to such an important question for us, whether we can speak of a universal average mathematical culture of society at all, and if so, what is essential for this culture, must be sought not only in "ready-made" mathematics, but also and even primarily in mathematical activity, and therefore the opinions and discussions of mathematicians themselves on this subject are important.
...

§5. Objectives of teaching mathematics

Society expects from its educational institutions effective results of their functioning. But in order to evaluate these results, one must have a clear awareness of the goals and postulated results of education in general and of mathematical education in particular.

In reality, the criteria for such an assessment corresponding to a given stage of mathematics teaching are often determined by the requirements of teaching mathematics at a higher level. In public opinion, a "good" primary school is a school that "prepares" its students well for secondary school, and a "good" secondary school is a school that prepares its students well for higher school. In this way, the goals of teaching mathematics at a certain level of school are practically defined ultimately depending on the requirements set for candidates for certain directions of higher education, and therefore depending on the needs of their small group in relation to the masses of students. Often, both the school and the teacher are even assessed according to the successes of a small elite of its graduates, without taking into account what the majority of average students, who will have to do with mathematics only to a small extent in their further studies or in their future profession, have gained from mathematical education.

Considerable attention is therefore devoted today to the theoretical analysis of what the teaching of mathematics in its three aspects of knowledge, method and language can contribute to general education, and in connection with this analysis to the specification of the potential qualifications which each pupil in a school covered by the school curriculum can acquire through learning mathematics. Various classifications and hierarchical systems of these qualifications are suggested by various taxonomies of general educational objectives.
...

§6. The first wave of reforms (1960s-1970s).

Current problems of democratising mathematics education, the importance of elementary mathematics "for everyone" in mathematics science, the goals of its teaching, the content, methods, means, evaluation of results, the position against aggressive anti-scientism on the one hand and "imperialism" of exact sciences on the other, must be considered against the background of the experience gained from the dynamic battalion concepts in this field, conducted over the last quarter-century. In particular, the reforms of the 1960s and 1970s, which were of enormous scope and significance, require detailed analysis of this knowledge.
...

§ 7. Second Wave Reforms

The decade of 1970-1980 in the history of mathematics education will be noted as a period of lack of stability, continuous fluctuations, sudden changes in the development of the concept of mathematical education, unrest, disorientation and dissatisfaction of teachers, and harsh criticism coming from different sides, of the programmes with methods and results of teaching, to which they were constantly subjected. One gets the impression that we are, and will always be, in the midst of a permanent mathematical reform of universal education, and this is perhaps necessary given the pace of change in science and technology, in social structures and in the living conditions of large numbers of people. When the Belgian Centre for Mathematics Pedagogy constructed, as it was called there, an edifice of elementary mathematics in the Bourbakist style, G Papy repeatedly emphasised that from the perspective of selecting content, its structuring and language, the problem of mathematical education in schools had been solved once and for all. The task of the teachers, apart from local improvements that did not destroy the fundamental idea, was therefore only to work out strategy and the correct introduction of this concept into school practice and the search for means and methods of making elementary mathematics thus understood more widely available to the masses. This opinion turned out to be an illusion, among other things because, regardless of the possibility of failure to implement this or another theoretical concept in school reality, it did not take into account changes in views on mathematics itself, its methodology and philosophy, resulting both from the internal conditions of the development of this discipline and its place and role in the dynamically changing world.

The main sources of the second wave of discussions on mathematical education and reforms undertaken in the decade 1970-1980 can be distinguished: 1. Criticism of the reforms of the previous period; 2. A certain shift in the directions of development of mathematics itself - as a science; 3. Modernisation of mathematics teaching in the initial grades /in elementary school/, which also entailed changes in the selection of material and its structure in post-primary grades 'post-elementary'; 4. Changes in school structures, and in connection with this, renewed discussions on programmes; 5. Growing opposition in developing countries to the import of school structures, curricula, methods and resources from developed countries, the conviction of the need to develop a concept of universal mathematical education, adapted to national needs, culture, traditions and economic conditions; 6. The growing role of computer science and digital machines.
...

§8. Conclusion

A review of the stages of development of views on what school mathematics should be for all or most reveals the enormous difficulties in developing such a concept. The experience of the last twenty-five years all over the world has taught us that it requires the fulfilment of - among other things - the following conditions.

1. It is necessary to be fully aware of who in a given country elementary mathematics in schools for all is intended for. It is necessary to know precisely the possibilities and needs of all youth and the possibilities and needs of society, current and in the perspective of the next twenty years.
   
   Without such a recognition, all concepts of education in general and of mathematics in particular, developed under the slogan of educational democracy, will remain either a paper document or will be implemented in practice leading to the degeneration of the idea and the democratisation of education. School teaching requires the organisation of a reduction that strengthens the barriers that hinder the educational advancement of a large part of the youth, and here the advancement is not measured only by the number of diplomas issued.
   
   
2. Importing foreign patterns without reliable analysis of their usefulness in local conditions is clearly harmful. However, isolation from foreign concepts and experiences from which both positive and negative conclusions can be drawn is also harmful. The movement of renewing the teaching of mathematics is an international movement, without joining this movement and using its experiences, developing concepts of mathematical education is deprived of a broader view of the issue.
   
   
3. It is necessary to clearly define the general goals of mathematical, universal education in local conditions and to orient all programme and textbook works towards the realisation of these goals and to evaluate the value of the concepts and products of these works from this point of view. Without this awareness and this orientation, programmes are constructed, among others, overloaded with mathematical content with the requirements of its full mastery by all students, which is a harmful fiction, leads to rote learning and not to the realisation of the general goals of "education through mathematics".
   
   
4. Elementary mathematics for all should not be a truncated or somewhat sanitised mathematics for the elite. It should not be mathematics "for the poor". Instead, it should be solid mathematics, modern in content, structure, and language at every stage of teaching. Failure to take into account this basic postulate leads either to "trump card" elementary mathematics, or to pragmatism and empiricism in the concept of elementary mathematics for the masses. "Trump card" mathematics contains, on the one hand, content that is unnecessary for everyone and introduced to the programme only for the sake of a further stage of education of the elite, and on the other hand, fundamental gaps that for this elite will be filled in the further stages of education, but for the majority will remain gaps forever. Pragmatic mathematics ceases to be elementary mathematics introducing the masses to the rudiments of mathematical culture. Elementary mathematics for all must be developed as a meaningful whole, allowing for insight into the duality of mathematics, so strongly emphasised by many mathematicians, useful for everyone and educating everyone.
   ...

The recently published work of Prof Dr Zofia Krygowska is a very valuable publishing item. Every mathematician and every teacher who wants to form a clear opinion about the value of our current mathematics programmes and textbooks and their new projects should read this book. It is especially valuable for all those who take part in the work and experiments. Here is the list of chapters of the work:

0. Introduction.
   
1. Democratisation of general education and school social selection.
   
2. The selective role of mathematics as a subject of teaching Critique of scientism and imperialism of mathematics in science and teaching.
   
3. Goals of teaching mathematics.
   
4. First Wave of Reforms (1960-1970).
   
5. Second Wave Reforms.
   
6. Conclusion.
   
7. Annexes.

The author presents a clear and reliable account of the concepts of universal mathematical education in various countries. First of all, she provides an outline of the general scientific and didactic ideas underlying the discussed programmes. However, she does not neglect to discuss the ways of approaching even specific topics wherever this approach characterises the fundamental position of the creators of the programme.

The work is documented with a huge amount of material, citing a hundred or so publications, including several-volume works. The author's long years of active participation in the international movement to modernise mathematics education deepen her view of printed materials, as it is based on direct contacts with outstanding people of different nationalities and views. From these documents, one can read the tendencies of educational activists who wanted to create modern mathematics for everyone in schools, legally covering all youth from 6 to 14 or 16, or even 18 years of age. The development of mathematics for everyone encounters various significant obstacles, including the selective role of mathematics as a subject of education - according to some - easier for children from more intellectually advanced environments. These children have earlier contact with everyday language in which abstract terms appear. On page 15 the author quotes the view of one of the educators: "The scientific and technical revolution has changed the type of snobbery. If in the years of Latin supremacy it was in good taste to emphasise one's humanistic education and even one's mathematical incompetence, now referring to graduating from high school in prestigious classes with mathematics as the main subject ... is often a manifestation of a new category of snobbery." In our country M Kozakiewicz writes: "Although it seems like a paradox, one can say that it is unfavourable for a child's development when they do not get into school, but it can also be unfavourable when, living in a disadvantaged environment, they get into schools that are rigidly focused on children from privileged family backgrounds."

Both teachers from developing and highly developed countries write about the difficulties resulting from social inequalities. Here is the voice of French teachers:

We are aware of the differences between children, because they are revealed every day in the classroom. But we do not want to take this too lightly. This imposes on us as the first goal of teaching during the period of compulsory schooling a negative goal, but an important one: not to discourage and not to bore; not to reject and not to discourage those who have difficulties, not to provoke a psychological block, not to bore those who achieve understanding faster (or so they think). We must also recognise that each child has their own rhythm, and currently the speed of achieving results plays a fundamental role in assessment.

Against the background of the views of outstanding mathematicians on the essence and cultural role of contemporary mathematics, the author refers to many interesting statements regarding the goals of teaching mathematics at school.

Presenting the different views of specialists on this subject, she places strong emphasis on the need to indicate specific paths to achieve these goals.

The general goals of mathematical education formulated in the texts of the programmes without specific programming of their implementation in the course of acquiring knowledge ... are empty slogans. The specific goals defining the knowledge, skills and abilities ... without their orientation towards general goals are - as Hans Freudenthal says - blind.

In connection with the analysis of these problems, the author critically refers to many issues related to the specific work of a teacher. Among other things, such basic issues as ways of developing the student's mathematical imagination and stimulating their activity. She also considers the problem of transferring the student's logical culture acquired in mathematics lessons beyond these lessons. This concerns, for example, the question of whether the student's habituation to the most precise and partially formalised language affects their way of expressing themselves outside mathematics lessons. In this work, we also have serious considerations on how curricula and requirements for students should be constructed so that they do not lead to learning certain knowledge and skills without developing the student's ability for mathematical activity, which is difficult to measure through objective assessment.

The main part of the book is devoted to a critical analysis of the reforms in mathematics education in the years 1960-1980. This period is divided into the first wave of reforms in the years 1960-1970 and the second wave of reforms in the following decade. The author discusses in a very interesting way the sources of the social, economic and pedagogical nature of the great wave of reforms that encompassed so many countries. She also writes here about changes in mathematics itself and about the separation of traditional school mathematics from mathematical science. She makes a reservation in advance that she deals only with the main - in her opinion - directions of reforms, because it is impossible to describe all the attempts at reforming mathematics education in the period under consideration.

After an objective discussion of the flaws of the system against which the reformers turned, the author characterises the four directions of reforms of the first wave that she has chosen:

1. Franco-Belgian and some similar reform projects in the United States,
   
2. English,
   
3. Soviet,
   
4. Japanese.

Before starting to characterise these programmes, the reader is generally introduced to the main international institutions dealing with the issue of teaching mathematics and the course of international conferences devoted to this problem in the years 1950-1970. The first of these models is discussed most thoroughly and extensively. The author writes:

The work preparing the reform was concentrated in both countries, Belgium and France, on the construction of elementary mathematics as a developed theory, largely deductive, integrated by basic set and algebraic structures, and on the creation of a new, specific language of school mathematics, both verbal and symbolic in the broad sense of the word, because in this language a drawing, a graph, a colour diagram played the role of specific symbols, interpreted according to sometimes ingenious conventions.

The Belgian conception ... is the most typical example of elementary modern mathematics in the Bourbakist style". The French conception differs from the Belgian conception, but it is also based on Bourbakist ideas.

The great variety of directions of reforms in the United States and the vehemence of the discussions accompanying them do not allow for such a brief characterisation. The author writes:

Most of the projects did not completely reject traditional content, but organised it in a new way. Plane geometry was integrated with spatial geometry, trigonometry was incorporated into algebra. The entire course was approached deductively as far as possible. Elements of the algebra of sets and relations were introduced, as well as general concepts of functions as elements integrating the entire construction. Elements of probability and statistics were included in the course of secondary school classes.

In England, too, one could observe a great variety of projects for the reform of mathematics education, however, as the author notes:

All projects have a common orientation: mathematics education is based primarily on solving problems with a wide consideration of simple applications, a deep-rooted distrust of abstractions and generalisations, a lack of interest in the deductive and structural approach to the teaching material, an emphasis on the intuitive approach and various motivations, including the connection of elementary mathematics with the everyday environment of the student, introducing fun, games, guesses, anecdotes into the process of learning mathematics.

In the USSR, a team of outstanding mathematicians and mathematics educators developed a programme introduced in 1967. The content of the old programme was enriched with elements of differential and integral calculus. On the other hand, elements of logic and set theory were very carefully incorporated into the programme. The latter is not mentioned in the programme itself, but in the comments to the programme, especially in connection with the study of digital machines. These comments also emphasise the appropriate balance of inductive and deductive elements in teaching mathematics.

In Japan, nine years (6-3) of undifferentiated education is compulsory for all children, 90% of whom go on to three-year general or vocational schools. "The mathematics course in the lower cycle is integrated by the concept of sets and functions, in the higher cycle plane geometry is organised axiomatically ..." The vast majority of ordinary students receive a very broad mathematical education.

The reforms of the second wave are characterised by a lack of stability, changes in programme concepts, sharp criticism of the reforms of the previous period, one of the main criticisms of the programmes of the 1960-1970s is their excessive abstractness and extensiveness.

The author writes:

... Teachers in this situation either implemented this programme without changes with strict selection of students, or implemented the programme only superficially, lowering the requirements to a minimum. This is an example of a general rule. If the programme is too extensive or too difficult, the teacher ... either implements it in full for a small group of the most talented students, or implements it either by applying only superficial requirements (learning by heart), or by lowering them almost to zero.

The author reports on heated, deeply understood programme discussions in the main countries where the reform of 1960-1970 had a Bourbakist character, i.e. in Belgium, France and the United States. Among other things, she provides the following recommendations for the 1980s formulated by the National Council of Teachers of Mathematics in Steinach, United States (NCTM):

1. Problem-solving should be the centre of school mathematics.
   
   
2. Basic mathematical skills should be defined so that they include not only arithmetic skills.
   
   
3. The mathematics curriculum should take greater account of the role of calculators and computers at all levels.
   
   
4. Requirements for the effectiveness of mathematics education should be strengthened.
   
   
5. The results of the curriculum and student progress should be assessed on a broader range of measures than conventional testing.
   
   
6. More mathematics should be provided to all students; flexible curriculum and a wider range of choices should be included in order to adapt teaching to the needs of a diverse student population.
   
   
7. Mathematics teachers should demand a high professional standard from themselves and their colleagues.
   
   
8. Community support for mathematics education should be raised to a level that is consistent with the importance of understanding mathematics for individuals and society.

The second wave of reforms in England has a different character and different sources. It is primarily related to the issue of democratisation of education. Programmes and methods of educating children in classes not differentiated by talent (age 7-13) are being developed, as well as methods of implementing programmes in older classes in three variants for students with different talents. The SMP Group presents a project of democratisation and education that is almost revolutionary for the English tradition.

In the Soviet Union, the modernisation of education was continuous. However, since 1978, there has been a violent discussion at the level of the Academy of Sciences on the content of the mathematics programme. The author reports on the issues that are discussed here. In each of the projects, the programme is very extensive, and the total time allocated to mathematics in grades 4-10 is 41 hours.

The author presents in detail completely unknown to us issues of teaching mathematics in developing countries. These countries, which in the first decade often imported ready-made programmes and even textbooks from developed countries, are now trying to build schools as adapted as possible to their needs and create their own versions of mathematics programmes.

The concept of mathematics for all, currently being implemented in the Hungarian People's Republic, is discussed in detail next. The mathematics programmes there have been developed and experimented with for a long time and give good results in practical implementation.

The book ends with characteristics of the work carried out in the Netherlands under the leadership of H Freudenthal and in Italy under the leadership of E Castelnuovo.

The four appendices to the book include:

1. Requirements for the first qualifying exam in England.
   
   
2. Skills and techniques that most students should acquire, according to the NCTM team in the United States.
   
   
3. The minimum that should be learned from teaching mathematics according to M S Bell (USA).
   
   
4. Basic mathematical skills according to the NCSM group (USA).

The book is very hard to find (only 200 copies). Therefore, contrary to accepted customs, I have quoted and summarised entire fragments and encourage those who can access it in libraries to read it.

Summary

Error is an instructive component of the development of human knowledge. "Errando discimus." If a misunderstanding comes to light in time through an error - it is a blessed error: it can and should be utilised for the student's progress. For this purpose a study of errors is necessary and will enable us to understand them better. First of all a clear distinction should be made between instant slips caused by the lack of attention or uncertainty, and deeply rooted incorrect reasonings. Also praxeologic and heuristic errors should be paid more attention to as they often lead to serious mathematical errors.

During many previous meetings organised by our Commission, in connection with various issues, problems of difficulties and errors in learning mathematics in their various aspects also appeared. Today we are focusing our attention on error in school mathematics, an error treated as the main subject of our considerations. We are therefore starting a global study that should enable us to better understand error from the point of view of its functioning in the process of learning and teaching mathematics. To better understand error in mathematics - this is the basic goal of our joint work.

Of course, we are not starting from scratch. On the contrary, various problems related to errors as essential and inevitable components of human activity have been comprehensively analysed since ancient times within the framework of philosophy, psychology, pedagogy, praxeology, and the history of sciences. The scope of these analyses and studies is so extensive and their results so rich that it is no longer possible to master with individual knowledge what has already been developed. So here we have a great opportunity to enrich this knowledge. However, it seems to me that it is equally important to take as a starting point our own experiences and observations made in the course of personal contacts with students and teachers. And this does not only concern works conducted with precision and methodological correctness. We hope that we will benefit greatly from the presentation of such works. But we should not underestimate more modest observations. Sometimes one fact, one example, seemingly isolated, even seemingly strange, is reflected in a sudden flash in our pedagogical intuition and can direct us towards problems of real importance. And from this point of view we have a great opportunity. We work in countries where the structures of school institutions, curricula, even concepts of mathematical education, and the conditions for their implementation, mentality, culture, economic status, and social history are very diverse. If certain phenomena that interest us here occur everywhere regardless of these differences, then these phenomena deserve special attention from our side. Their existence testifies to the specific nature of mathematics as a subject of learning, which - perhaps - is not yet well taken into account in our pedagogy. On the other hand, phenomena that seem to be consequences of specific situations are particularly instructive. On the basis of both this consistency of facts and their diversity, we can get closer to what is essential: to understand error better in the light of its multidimensional analysis.

Since ancient times, error has been treated not only as a natural, inevitable component of human activity (humanum est errare), but even as a positive, instructive component of the development of knowledge, learning, and creativity (errando discimus). Error should not therefore be considered a misfortune, a catastrophe, neither for the one who learns nor for the one who teaches. So why is it different in school conditions? In seeking an answer to this question, we should - among other things - reflect deeply on the nature of mathematics as a subject of learning and teaching. Regardless of the external organisation of learning mathematics, even in a situation where this organisation is loose, wide open to spontaneous development, a priori unplanned, mathematics as a subject of learning retains its internal organisation. It is a field conceptually organised by itself so that a seemingly small gap in understanding or knowledge can easily provoke further misunderstandings, growing one on top of the other, which manifest themselves in an avalanche of errors, difficult to stop. A small calculation mistake can turn a simple exercise into a difficult problem. A student who gets lost in such complications falls into various traps, makes mistakes. Mathematical activity requires special attention, constant effort of self-control, the ability to use specific techniques of such self-control, which a beginner in mathematical activity has not yet developed. The language of mathematics at every level of learning creates possibilities of misunderstandings and the danger of separating this language from its semantic meanings. The process of learning - teaching mathematics requires - among other things - overcoming various contradictions, for example the one that opposes the need for automatic mastery of algorithms to the need for constant development of non-algorithmic thinking, or more generally the one that opposes skill in using procedures to clear awareness of facts, or the one that opposes natural everyday thinking to more or less formal thinking, based on conventions often artificial for students.

At the dictionary level, an error is defined by referring to "truth" or "reality", or from a praxeological point of view to the "purpose" of the action. But what is the truth that the child violates by calculating $3+2 \times 7 = 5 \times 7 = 35$? Of course, it is only a convention, not at all natural for those who are accustomed to reading other texts from left to right. But is such a common error, seemingly similar, $3x+2y = 5xy$ - just a failure to observe the convention? What truth, what reality are we talking about here?

Of course, the process of learning - teaching mathematics has its deep roots in the realities in which the student lives and acts: biological, physical, social, economic, cultural reality... We start from these realities and constantly return to them. These realities connect, interpenetrate simultaneously. On the other hand, learning mathematics takes place - among other things - in passing from one mathematical reality to the next, with crossing and overcoming more or less difficult conceptual thresholds. The transition from the world of natural numbers, so close to the child, to the rich world of numbers is a radical change in mathematical reality. The set organisation of geometric space is also a radical change in the original Euclidean reality. The child does not perceive a square as an infinite set of points. He perceives a square globally as a spatial form. Teaching changes this natural reality into a new reality. Some observations conducted in high school classes, called "university" (intended for students gifted in mathematics), show how many traps provoking errors are created by the set organisation of Euclidean space, even for students who are so gifted. Many people, not only students, who are already familiar with set operations in geometry, incorrectly solve the task formulated in the school textbook in the chapter devoted to Thales' theorem and the properties of homothety, because the global Euclidean vision inhibits local set analysis.

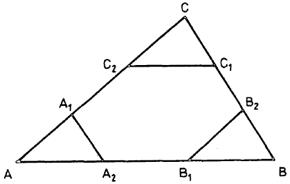
Here is the task: From the triangle $ABC$ triangles $AA_{1}A_{2}, BB_{1}B_{2}, CC_{1}C_{2}$, homothetic to the triangle $ABC$ in the ratio of $\large\frac{1}{3}\normalsize$ with respect to points $A, B, C$, respectively, are subtracted. Does the figure resulting from this operation have a centre of symmetry? The answer is usually positive, the centre of symmetry is immediately indicated, which is false in the plane organised in set terms, but correct in classical Euclidean reality. From this last point of view, what remains after subtracting (in the Euclidean sense) three triangles is a hexagon with a centre of symmetry. From the set point of view, however (set subtraction), the resulting figure is not a hexagon and has no centre of symmetry.

In the new mathematical reality, certain associations, certain intuitions, certain habits that were previously established, function for a very long time. A child who moves from the world of natural numbers to the world of other numbers has difficulty getting rid of the belief that addition and multiplication are "augmentation". According to one of the psychological laws, associations are established quickly, but the period of their elimination is much longer. Misunderstandings and the errors they cause are natural and inevitable phenomena when crossing the threshold leading to a new mathematical reality. On the other hand, misunderstandings that are established, persistent and hidden are dangerous. What is more, it can be said that in many cases such hidden misunderstandings work retroactively in the sense that they disorganise what has already been correctly mastered. The student begins to make mistakes that he has never made before.

This is not the right time for a broader discussion of these topics. By raising them, I only want to strongly emphasise that in our multidimensional analysis of errors, the dimension of "the nature of mathematics as a subject of learning" should be taken into account very deeply. It is easy to indicate as the causes of difficulties, misunderstandings, errors made by students, our errors in teaching, bad programmes, bad textbooks, etc. But the answer to the question of why all this is bad, and how to improve what is bad, requires - of course, among other things - deep reflection on this dimension. Our observations of school reality show that the lack of awareness of the specificity of mathematics as a subject of learning and teaching makes it difficult to choose the right preventive measures and effective therapy for errors.

Here I come to the fundamental problem of our pedagogy, the concepts of prevention and therapy of errors. I would prefer to speak of prevention and therapy of possible misunderstandings and false concepts that manifest themselves in the form of errors. But this is not about terminology. Learning mathematics is not a continuous process. Prevention, on the other hand, should be a continuous component of the teacher's activity. Teaching mathematics requires a dialectical attitude on the part of the one who organises the learning of mathematics by others, an attitude that combines trust in the students' abilities with distrust of their ability to avoid dangerous superficial associations and false concepts. Didactic prevention, which consists of anticipating possible misunderstandings and preventing them, is deeply connected with the reasonable, didactic use of errors. "Errando discimus." If a misunderstanding manifests itself early enough, I emphasise: early enough, in the form of an error, then it is a "blessed error" that can and must be used for progress. But often a misunderstanding remains hidden for a long time. The student's behaviour may be completely correct for a long time, even though his concepts are false. How to reveal a misunderstanding in time? To provoke a mistake, to deliberately create tricks? It sounds unpedagogical, ugly. But it can be done honestly in the course of solving problems. I think we will discuss this issue, which I consider particularly important.

Prevention in relation to misunderstandings and errors in learning mathematics is directed from what is happening in the classroom today to what may result from it in the future; therapy, on the other hand, from what is happening today to what has happened before. In order to "cure an error", one must know what the error is a symptom of and what its sources are. A significant error in mathematics (i.e. not just a momentary mistake) is not isolated from other errors. Errors with the same roots create entire families, even structured families. Studying such a family often allows one to detect the roots of the error, which is very difficult when we deal with a single error in isolation from others. Error therapy should not be identified with its apparent elimination. However, observation of school reality reveals that as a result of such apparent elimination (prohibitions, orders - the student does not make a given error, but still does not understand the essence of the matter) new misunderstandings and errors arise. I hope that we will discuss these problems in more detail, based on research conducted in various mathematical situations.

The conference programme asks us questions about the classification of errors. These are not just academic questions. It would be better to talk about a typology than about the classification of errors. Attempts at such a typology can be made from different points of view. However, when considering these issues from the point of view of prevention and therapy of errors, we should not ignore the simplest typology - in my opinion - important. We cannot throw into the same conceptual bag, on the one hand, the attitudes and behaviours of a student who says or writes anything because he is not interested in solving the problem, momentary mistakes caused by lack of attention, errors resulting from gaps in knowledge that can be easily corrected by the student himself, if he is given time to reflect or supplement his knowledge, 'conclusions based' on reckless guessing, etc., and on the other hand, conscious reasoning that is logically incorrect, and errors that reveal deeply rooted false concepts that the student even stubbornly defends if we allow him to do so. Of course, the teacher's reaction in these two different situations must be completely different. This statement is trivial - it is true. But I would like to emphasise very strongly that this banal pedagogical principle is not always implemented in school practice. In order to distinguish a mistake from a significant error, you need to have time, you need to treat each student individually, and most importantly, the student must have full trust in the teacher, you need to eliminate the fear of error. All this is very difficult in overcrowded classes, with mandatory and overloaded content programmes, not adapted to the capabilities of the average student. In such situations, an error becomes a disaster for both the student and the teacher.

Our students make many mistakes due to inattention and lack of self-control. In what sense can we speak of prevention and therapy in relation to such mistakes? Of course, mathematical activity requires the use of various specific self-control procedures. These techniques are closely related to the multifaceted understanding of the mathematical domain of this activity. Do we teach mastering such self-control techniques in mathematics education? Is this problem really taken into account in didactic theory?

Our students make many praxeological errors. This issue was not highlighted in the programme of the current conference, but it deserves our attention and discussion. Errors of this type also lead to mathematically significant errors. Psychologically, it is understandable that a student lost in complications resulting from the lack of praxeological order in solving a task also begins to make mathematical errors.

I should finally make a remark to avoid misunderstandings. I do not think that mathematics is a more difficult subject than other subjects. On the contrary, I believe that in some areas of learning greater difficulties are encountered than in learning mathematics. But in these areas many misunderstandings are often not revealed as clearly as in the course of learning mathematics. They remain hidden behind the barrier of verbalism. I only want to emphasise that in our research we must constantly think, on the one hand, about the specificity of mathematics as a subject of learning, and on the other hand, about school reality as it really is, and not in the postulates of pedagogical theory.