Shortest path joining three points

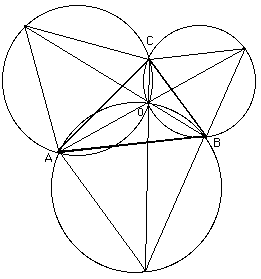
If the triangle $ABC$ has an angle, say at $A$, greater than 120° then the shortest path is $B$ to $A$ to $C$. If all the angles are less than 120° then the sum of the line segments $AO$, $BO$ and $CO$ is the shortest path (See figure). Torricelli showed that $O$ is the point of intersection of the circumcentres of the equilateral triangles drawn on the three sides. Cavalieri showed that the line segments of the paths form angles of 120° at $O$. Simpson showed that the line sgments joining each vertex of the triangle to the opposite vertex of the equilateral triangle intersect at $O$. The lengths of each of these line segments are equal to the minimal path length $AO + BO + CO$. Fasbender showed that this minimal path length was equal to the maximum of the latitudes of all equilateral tringes circmscribed about $ABC$.