Minimal path between two points via a line

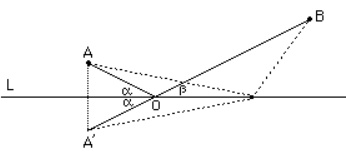
There is a unique shortest path from $A$ to $B$ reflecting in the line $L$. It is seen in the diagram that the angles of incidence and reflection ($\alpha$ and $\beta$) are equal for this shortest path. The variational priciple here gives the well-known law for the reflection of light (and billiard balls!).

It was known to the Greek mathematician Heron of the first Century AD and it appears as a problem in his book Catoptrica.