Simple Harmonic Motion

For small swings of a pendulum, the displacement

x

satisfies the differential equation

\Large\frac {d^2 x}{dt^2}\normalsize = -k^2 x

where

t

is time and we ignore frictional resistance.

This is called Simple Hamonic Motion or SHM.

This has a solution (which we may as well assume is 0 at

t = 0

) of the form

x = A \sin(kt)

with

A

constant.

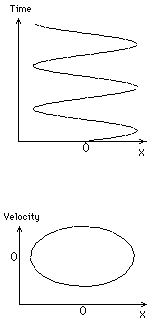
So the graph of

x

against

t

is a sine curve.

If we plot

x

against the velocity

\Large\frac {dx}{dt}

then we get a curve in what is called the phase plane. For this case the curve is a closed curve and is in fact an ellipse.