Henry Perigal's mathematical and astronomical work
We present below some extracts from Henry Perigal's writings and some extracts from reports about talks and demonstrations that he gave. They are roughly in chronological order, but often refer to ideas from many years earlier. We note that in places Perigal uses words of his own making such as 'orbitation', 'orbitate' and 'spiralite'.
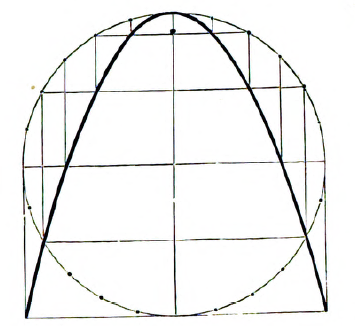
1. Discovered in 1835.
With Radius draw a Circle, and its Diameter for axis of . Take any arcs from one extremity of the diameter, and bisect them. Draw from the arcs , lines () perpendicular, - and, from the half arcs, lines () parallel, - to the diameter. These parallels and perpendiculars meet or intersect in the curve of a PARABOLA, whose equation is ; with Base = Axis, Parameter = half , and distance of Focus from Vertex = one-eighth of .
2. Literary Gazette, 28th March 1846.
At the Marquess of Northampton's soirée, on Saturday, 21st of March 1846, amongst the several objects of interest exhibited, and in some instances explained, to the numerous visitors, the following chiefly attracted our attention: - Mr Perigal's instrument to develop a peculiar law of compound motion, generating retrogressive or recurrent curves ... By the instrument, Mr Perigal developed a peculiar law of compound circular motion, "generating retrogressive or recurrent curves, by which the moving body, when it has reached the extreme points of the curve, retrogrades or returns back in exactly the same line along which it advanced; constantly moving forward and backward from one extremity to the other; and always tracing and retracing the same line as it alternately advances and recedes.
These curves were produced by a complicated system of wheel-work, which Mr Perigal stated to be capable of generating numberless varieties of curves dependent upon the ratio of the velocities of the movements; but the instrument was, on this occasion, adjusted for the production of parabolas or hyperbolas, and a sort of figure of 8 curve resembling a lemniscate, which he showed to be different forms of one and the same curve, just as circles and right lines are (limits or) varieties of ellipses. When the tracing-point passed through the centre, the curve was at one of its extremes or limits; and the two ovals of the figure of 8 were opened to their fullest extent of roundness; but alterations in the angular adjustment of the movements caused these ovals to become more and more flattened, till they ultimately converged or collapsed, and became in appearance a single line, terminating in points, with the form of a parabola or hyperbola; and the tracing-point travelled forward and backward from one extremity of the curve to the other repeatedly, without in the least degree thickening the line in one part more than in another; evidencing that it advanced and receded in exactly the very same path! In fact, the line of return might be considered as superposed upon the line of advance; as Mr Perigal remarked , in reply to a very eminent mathematician, who objected that the figure of 8 curve was a line of the fourth order, inasmuch as it could be cut by a straight line in four places, while the parabola was a line of the second order, because it could be so cut only in two places; but the suggestion of its being a double line superposed seems to remove the difficulty.
Mr Perigal mentioned that one of his objects was to exhibit the PARABOLA in the novel character of a retrogressive or recurrent curve of definite range; whence he inferred, that if a comet moved in that curve (as most of them are said to do) it might return after it had performed its allotted journey, and continue to visit us periodically; as several do, which are therefore supposed to travel in very elongated ellipses, although their apparent path more resembles a parabola.
We do not take upon ourselves to decide that this "retrogressive" curve of Mr Perigal is or is not identical with the parabola of Apollonius, but we can bear testimony to its striking resemblance to the conic section; affording at least prima-facie evidence of its relationship, however much its newly discovered property of "periodicity" may shock the prejudices of those who have hitherto thought themselves learned in such matters. Besides, it is well known that reciprocating straight lines can be produced by combinations of circular motions; and, therefore, we cannot see why it should have been deemed impossible so to produce parabolas and hyperbolas, which, being curved lines, would even appear the less unlikely. Of the importance of the discovery in reference to the cometary theory, our scientific readers will judge for themselves; and such of them as are mathematicians can, for their own satisfaction, put the question to the proof by submitting the problem to analytical investigation. - Literary Gazette, 28th March, 1846.
3. Literary Gazette, 7th April, 1846.
At the next subsequent soirée (4th of April 1846), was exhibited another new instrument of Mr Perigal's, for the practical development of
ANOTHER NEW LAW OF COMPOUND MOTION,
proving that the parabola occurs as a branch, or component part, of a great variety of curves. This he showed by a modification of Professor Wheatstone's photometer; the curve selected being a trochoidal curve of eight symmetrical loops, which became eight cusped branches, or eight hyperbolic, or eight parabolic branches, etc. varying according to the radial adjustment of the bright steel ball representing a comet or planet; which, in this case, always moved in one and the same direction, instead of alternating in opposite directions, as in the experiment exhibited at the previous soirée. Mr Perigal explained that, besides multitudes of other kinds, there are innumerable varieties of this particular kind of curve, having any imaginable number of symmetrical branches, approximating more or less nearly to the ellipse and parabola; in other words, that these are curves of which the ellipse, the hyperbola, and parabola, are limits or particular cases.
It seems to result, then, from these experiments, that it is not impossible for comets to return periodically, either forward and backward alternately, or always in the same direction, although moving in "curves which cannot be distinguished from parabolas;" quite as possible, indeed, as if they moved in elongated ellipses. (The consideration of the forces requisite to maintain them in such orbits is of course a totally distinct question.) That is to say there is nothing in the nature or properties of the curve itself to render the comet's periodical return impossible, now that the attribute of infinity, ascribed to the curve, is no longer admissible, except to express only the extreme or limit of the curve; just as a straight line may be imagined capable of infinite extension, but nevertheless may be drawn of any requisite degree of shortness, and is still a right line whether short or long. - Literary Gazette, 7th April, 1846.
4. Morning Post, 6th April, 1846.
Mr Henry Perigal, literally, as well as figuratively, made a considerable noise among the learned with a piece of clock-work, which kept a small steel ball, representing a comet, in very rapid motion, in a curve of a very curious and beautiful figure - a sort of eight-rayed star, of which the eight branches were of a parabolic form. This, we understood, was intended to prove that a comet might return along the same path, and continue to visit us periodically , although moving "in a curve which cannot be distinguished from a parabola." This experiment differed from one he exhibited at the previous soirée, inasmuch as the curve then shown had but one branch instead of eight; and the comet moved alternately in opposite directions, backwards and forwards always in exactly the same line), while in the present case the comet continued to move always in one and the same direction. These discoveries of Mr Perigal are especially interesting and important at the present time, when so many as five comets have been visible at once in the starry firmament. - Morning Post, 6th April, 1846.
5. Literary Gazette, 20th February 1847.
ON THE REVOLUTION AND ROTATION OF THE MOON.
At the soirée held at the house of the Marquess of Northampton, President of the Royal Society, on the 13th of February, 1847, Mr H Perigal exhibited and explained a variety of experiments, with a view to elucidate the theory of Revolution and Rotation, especially referring to the (hypothetical) motions that have been attributed to the Moon, to account for her presenting towards us always the same face or hemisphere. One of his instruments imparted to three ivory balls movements similar to those ascribed to the Moon in each of the three following hypotheses: and the resultant paths, which the component atoms of the Moon would in each case describe in space, were made evident to the eye by an other little instrument which he called a Kinescope. With the aid of maps, on which were accurately laid down the positions of the Moon in accordance with the several hypotheses, these instruments and other auxiliary contrivances afforded ocular demonstration that, of the three, the last is the only one that will bear investigation.
1st hypothesis. That the Moon revolves round the Earth, and rotates on her own axis, in the same period, and in the same direction. These two circular motions would cause every individual atom of the Moon to move round the earth in a separate curve of the cardioid kind: these curves would vary in phase and dimensions according to the relative distance of each atom from the axis of rotation, and they would intersect in all directions. - In this case, the Moon, every time she travelled round the earth, would hare two alternations of sidereal day and night, but only one alternation of terrestrial day and night; because, as regards the Stars which are outside her orbit, she would turn round twice, once round the Earth, and once round her own axis: but, as regards the Earth, which is inside her orbit, she would turn round only once; inasmuch as her orbital motion is a movement of migration or translation, which alters her bearing, but not her aspect to the Earth round which she revolves. - Consequently, if the Moon were, simultaneously, to revolve around the Earth and to rotate about an axis within herself, with equal angular velocities in the same direction, all parts of her surface must be presented successively towards the Earth in the course of each rotation; as the inevitable result of such double motion.
2nd. That the Moon revolves round the Earth, and rotates on her own axis, in the same period, but in contrary directions. - These two circular motions would cause all the component atoms of the Moon to describe in space separate circles, all of the same size, intersecting in every direction. - ln this case the Moon, each time she revolved round the Earth, would have one alternation of terrestrial day and night, for the same reason as before explained; but no alternation of sidereal day and night: became, as regards the Stars outside her orbit, the turn she makes in one direction round her own axis counteracts the other turn she makes round the Earth. If the two axes were coincident, the two motions would destroy each other, and apparent rest would ensue; but in this instance they would neutralise each other so far as this particular effect of turning round: consequently she would maintain what is called the parallelism of her diameters, a result which, hitherto, has been attributed erroneously to the action of one circular motion (revolution) alone. - Consequently, if the Moon were, simultaneously, to revolve around the Earth and to rotate about an axis within herself, with equal angular velocities in contrary directions, all parts of her surface must be presented successively towards the Earth in the course of each rotation; as the inevitable result of such double motion.
3rd. That the Moon revolves round the Earth, but does not rotate on her own axis. - This single circular motion would cause all the component atoms of the Moon to describe round the Earth concentric circles varying in size according to their radial distance from the centre of revolution. - In this case the Moon would have one sidereal day and night every time she revolved about the Earth; because she would thereby turn round as regards the Stars; while her aspect to the Earth being unchanged by her orbital motion, she would have no alternation of terrestrial day and night. - Consequently, if the Moon were to revolve about the Earth, without any additional rotation on an axis within herself, the same hemisphere must be presented constantly towards the Earth, as the inevitable result of such single motion; and we should see the same face invariably, as we do now.
Thus it was rendered evident to the eye, as well as to the mind, that the last hypothesis may be true; but that neither of the others would produce the effect that, hitherto, has been attributed to them by their respective advocates.
Wherefore, if the Moon orbitates about the Earth as its Satellite, any additional rotation in the same or in the contrary direction around her own centre of gravity is physically impossible; if it be true that she always presents towards us the same hemisphere, a fact which there seems no reason to doubt. Or, if she rotates on her own axis, she cannot also revolve about the Earth as her only centre of orbitation. - She cannot partake of both the circular movements in question, be they termed revolution and rotation, or distinguished by any other appellations: but, if our Satellite, she must orbitate around the Earth without any rotation on her own centre of gravity or about any axis within herself. - Consequently her libration is not caused, as asserted, by the inequality of two such movements; and remains to be accounted for. -If the Earth were her Satellite, she might rotate on her axis in the same period and in the same direction as the Earth revolved round her. - See Literary Gazette, 20th Feb. 1847.
At the Marquis of Northampton's soirée 13th of March 1847, Mr Perigal exhibited several of his kinescopes, producing spiralites and convolutes, certain curves which "progress" in spires (coils, or circumvolutions), so that any portion of any such curve is a portion of a spiral. Mr Perigal explained that some of these curves were "interminate," or capable of unlimited extension, such as the spiral of Archimedes, etc.; others finite, "returning into themselves" at the termination of their respective cycles, to reiterate the same path in the same direction; each forming (when completed) a continuous line, of which all the component parts are spiral. Of these finite curves there are, according to Mr Perigal's account, innumerable varieties, distinguished by the number of their spires, and of their loops ; the most simple being produced by the combination of two circular motions, of which the curves he exhibited were examples. Whence, Mr Perigal asserts, the property of infinite extension, hitherto ascribed to all spirals, is applicable to comparatively a few kinds only; a vast majority of spirals being parts of curves, which curves (if completed) return into themselves. Literary Gazette, 20 March 1847.
6. Written 23rd December 1856.
THE MOON CONTROVERSY. FACTS v. DEFINITIONS.
The fallacy combated in what is called the Moon Controversy has now existed about two centuries: having been propounded by Galileo; who, in his zeal to facilitate the adoption of the Astronomical system of Copernicus, originated the dogmas objected to by myself, and others, who deny the possibility of the Moon's rotation if she be the satellite of the Earth.
...
While travelling round the Sun, the Earth has a second movement about its own centre of gravity, called its rotation on its axis; which causes the alternations of day and night, by turning all sides in succession to and from the Sun: noon or midnight occurring at any place on the globe whenever it comes into the plane which passes through the axis of rotation and the straight line joining the centres of the Earth and Sun; when the Sun is said to be on the meridian. Some say there are as many rotations of the Earth ... there are solar days (): others contend that the number of rotations equal the sidereal days (). The Planets likewise are said to rotate on their axes. And the Moon also is imagined, by some, to have a similar rotation about her axis, while travelling round the Earth. Many, however, besides myself conclude that the Moon cannot rotate on her axis, because she does not show all sides to the Earth, as the Earth turns all sides to the Sun, to the Moon, and to the Stars, every time she rotates: but others (till lately a majority) contend that the Moon rotates in the same direction, and in exactly the same period, that she circuits the Earth, in order to prevent her turning all sides to the Earth! This latter hypothesis has been refuted, of course, repeatedly: but nevertheless is still persisted in by most of the authorities; which continually gives rise to controversies, as at present.
...
Astronomers maintain that the Moon rotates upon her axis in exactly the same interval that she requires to perform R. circuit round the Earth; that is in one sidereal period of 27d 7h 43m: and that the two movements are in the same direction, from west to east, like the hands of a watch. Moreover they assert that "the Moon's rotation is uniform, that is, it is always performed at the same rate, and therefore in the same time; but her motion round the Earth is not invariably at the same velocity in all parts of her orbit: consequently the line joining the centres of the Earth and Moon fluctuates a little in its position, so that the same identical point of the Moon's surface is not always the centre of her disc, and we gradually get sight of a zone of a few degrees in breadth on all sides of the border, beyond an exact hemisphere, by means of these librations.
It is clear, therefore, that they attribute to the Moon a double motion, compounded of two distinct movements, round different centres, separated from each other by the distance of the Moon from the Earth. The centre of one of the two movements being the Earth's centre of gravity; while the Moon's centre of gravity is the centre of the other movement. We, on the contrary, say that she has only one of these movements - not both: if she has the first of them (that round the Earth), she cannot have the second also.
The question is not whether such movements should be termed two rotations or two revolutions; or, more correctly, a rotation and a revolution round separate centres; but whether both movements co-operate to produce the result, or whether the effect is produced by only one of them.
The controversy, therefore, is not a question of words - but of facts: facts of no small importance to the science of astronomy. No one denies that the Moon turns round to the Sun and Stars, though not to the Earth. Why she does so? - is the question: how she turns, and what she turns round? - is the fact controverted, and the problem to be solved.
Those who deny the rotation of the Moon maintain that parallel motion in a circle is compounded of at least two movements round separate centres. While those who affirm that the Moon rotates assume as the base of their arguments, that if she orbitated around the Earth without also rotating, she would maintain parallelism, inasmuch as they assert that parallel motion in a circle is a simple and not a compound motion. The Moon controversy, therefore, is resolvable into the question "Is parallel motion in a circle a simple motion, or is it a compound motion?"
That the Moon always presents towards the Earth the same portion of her surface so that one half of the Moon has never been visible to the Earth, nor the Earth ever been seen by the inhabitants of that hemisphere of the Moon - is an acknowledged fact: but her rotation, as the cause assigned for it, has long been disputed. Instead of the Moon's rotation producing that result, it would have the contrary effect, by turning all points of her surface to the Earth, as well as to the Sun and fixed Stars; just as the Earth turns all sides to the Sun and Moon, as well as to the Stars, during each daily rotation. Like causes (in like circumstances) always produce like effects: and therefore if the earth has one sidereal day for each revolution round the Sun, in addition to one solar day and one sidereal day for each of its rotations round its own axis, the like effects must be produced by the analogous revolution of the moon round the earth. Consequently, we affirm that the Moon has one sidereal day every time she resolves around the Earth, because she revolves, and by revolving turns herself round; while she always presents one same hemisphere towards the Earth, because she doe not rotate, or turn round any axis within her own body. She has but one movement, not two. Her motion is single, not double.
Henry Perigal, Junr.
26 Brompton Square,
23 December 1856
7. Astronomical register 7 (1869), 68-69
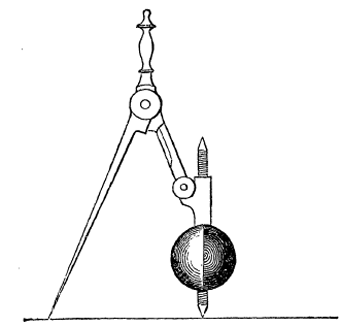
REVOLUTION AND ROTATION ILLUSTRATED BY BALL AND COMPASSES
When the Ball and Compasses are turned round on the point of the axis passing through the ball, the ball rotates; when turned round on the point of the other limb of the compasses, the ball revolves. These are the two modes of turning round. Both are simple motions, each being a single movement; and each causes the ball to turn all sides to the spectators, but to present constantly the same hemisphere to the other limb of the compasses.
Revolution and Rotation.
In tracing a circle with a bow-pen or a pair of compasses, both limbs of the instrument simultaneously turn round the same centre; and while both face in succession every point of the horizon, each retains the same face to the other. A ball with one hemisphere red or black and the other white on a screw axis, substituted for the pencil, makes the effect of the two movements more conspicuous, demonstrating that each of them shows the same face to the other, but all sides to surrounding objects - one in consequence of its axial rotation about the fixed centre of the circle described by the other, and that other in consequence of its orbital revolution round the centre of rotation of the former. These movements exemplify the two simple ways of turning round, viz.: - axial rotation round a centre or axis within the body; and orbital revolution round a centre or axis not within the body, but more or less distant from it. Thus the Earth is said to revolve round the Sun once a year, while it rotates on its axis every day. This being the distinction between them, it is obvious that rotation may be regarded as the limit of revolution, and revolution the extension of rotation.
If the ball be rotated on its screw axis (as in screwing or unscrewing), the white and coloured hemispheres will alternately be turned towards the other limb of the compasses - thus affording an infallible test whether or not the ball turns on its axis.
Due consideration of this simple experiment ought to convince anyone that if the Earth travels round the Moon, the latter turning round her own centre in the same time and in the same direction would have the effect of turning one hemisphere always towards the Earth, while turning all her surface to all surrounding objects except the Earth, - but that, if the Moon travelled round the Earth as alleged, turning round her own centre must have the reverse effect as regards the Earth, as it would cause every part of her surface to he turned towards the Earth (as well as towards all surrounding objects)in the course of each rotation; whether she turned round her axis or centre in the same direction as she travelled round the Earth, or in the contrary direction; and whether she thus rotated once in each circuit, or oftener, or not so often. These are the natural effects of turning round; as anyone, to whom such results are not self-evident, ought to fully understand after studying what the experiment teaches.
57 Warren Street, Fitzroy Square, W.
HENRY PERIGAL.
8. Written 12th October 1871.
KINEMATIC ASTRONOMY OF THE PAST AND FUTURE.
The Ancients aa well as the Moderns must have noticed that the Planets increased and diminished alternately in apparent size; and no doubt attributed the variation to the periodical change of distance.
It was further noticed that the motion of the Planets was not uniform nor continuously in the same direction; that their apparent progress was sometimes faster, sometimes slower, that they were occasionally stationary for a time and even retrograde; and that these incidents occurred periodically. It was soon found, however, that all these phenomena could be readily accounted for by assuming that the Planets had a second circular movement within the zone of space to which their wanderings seemed restricted. The investigation of these facts etc. probably led to the adoption of the Epicyclic System of Ptolemy and Hipparchus; and will eventual1y lead to its revival as the Astronomy of the Future.
About sixty years ago, Cassini made systematic observations of the principal Planets, with a view to ascertain their geocentric orbits. Taking for granted that when at their greatest apparent magnitudes they were nearest 10 the Earth, and farthest from it when at least magnitude, and that their intermediate variations of magnitude were proportional to their geocentric distance, he made maps of their successive positions and apparent magnitudes; and found thereby that their geocentric orbits were looped curves, of which he published rough diagrams. These Curves are Epicyclic Curves, now called Bicircloids, from their being resultants of two circular movements; and the annexed figures, traced by machinery, are authentic representations of Kinematic Curves to which the Cassini Orbits approximate.
Of course they are only exhibited as representative types of the respective Curves. The real Curves of the planetary orbits do not return into themselves until after ages of ages of revolutions in their orbits, if they ever do so at all; but they periodically retrace nearly the same paths they had previously traversed, in a zone of space bounded by the apocentral and pericentral circles of which the Earth is the centre.
Henry Perigal
9 North Crescent, Bedford Square
12 October 1871
9. Messenger of Mathematics (2) 1 (1872), 103-106.
ON GEOMETRIC DISSECTIONS AND TRANSFORMATIONS.
By Henry Perigal, F.R.A.S., etc.
The present series of papers consist chiefly of notes and diagrams extracted from my note-books and sketches made during the last forty years. I have devoted much time and thought to the solution of geometric theorems and problems by dissections and transpositions, viz. in proving the equality of areas in equivalent rectangles, etc., and investigating how the figures could be best dissected, so that their component parts might be fitted together in either form, and I have often contemplated proving all the suitable Theorems and Problems in Euclid by such dissections and transpositions, so as to render them self-evident by ocular demonstration.
I worked on paper ruled all over in small squares, which I found useful in facilitating dissections; and I have always had a fancy that the ancient Egyptians and early Greek geometers adopted some such expedient in their geometrical researches. So that I deem it probable that the property of the right-angled triangle may have been discovered by similar means; and the solution I hit upon forty years ago was perhaps the very one discovered forty centuries ago, and re-discovered by Pythagoras nearly twenty centuries afterwards; and not unlikely, as was also the case with me, in the endeavour to find geometrically a square demonstrably equal in area to a circle by dissection and transposition.
On recently showing some of my notes and diagrams to Mr J W L Glaisher he expressed a desire that I would contribute a series of short papers for the Messenger of Mathematics, containing selections from them; and this I have great pleasure in doing. I commence, therefore, with my best demonstration (to be followed by others) of the famous proposition, known as Euclid 1. 47, by dissection and transposition; in which it will be seen that the square on the hypothenuse is very simply and symmetrically dissected into five parts (only) that can be transformed into the squares of the other two sides, the smaller of them being intact, and the larger divided into four symmetric quarters. It was discovered by me about 1830, I think; and was printed in 1835, with a Euclidian demonstration by Mr William Godward, for private circulation among my friends, but has not hitherto been published, so far as I know, except as a diagram on my card, and as a dissected puzzle, of which I have given away hundreds.
The manner in which I enunciated the problem in 1835 was as follows:
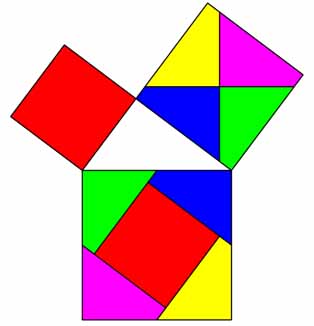
Mechanical Demonstration by the transposition of parts, of the Theorem of the Right-angled Triangle. Let ABC be a right-angled triangle, having the right angle ACB; the square described on the hypothenuse AB is equal to the sum of the squares described on the perpendicular AC, and on the base CB. Through the centre of the square of BC draw two straight lines, the one parallel and the other perpendicular to the hypothenuse AB; which will divide the square of BC into four equal parts. From the middle of the sides of the square of the hypothenuse AB draw, till they meet each other, four lines, two of them parallel to AC, the others parallel to BC; which lines will enclose a space equal to the square of AC, and will cut off from the corners of the square of the hypothenuse AB four portions, each equal to one of those into which the square of BC was divided.I will now give the proposition with its demonstration.
Proof of Euclid 1. 47, by Transposition of Component Parts.
Through the centre of the square of the base draw two straight lines parallel and perpendicular to the hypothenuse, and through the middle points of the four sides of the square of the hypothenuse draw the four lines parallel to the sides of the triangle as in the figure. One of the lines cutting the square of the base, through the centre, being parallel to the hypothenuse and bounded by the same parallels and the other line cutting it at right angles being also bounded by equal parallels - the four segments are each equal to half the side of the hypothenuse square, which is thereby divided into four symmetric quarters. The sides of the quadrilateral 1 being each parallel to the analogous sides of the quadrilateral i, and two of the sides of each being equal to half the side of the hypothenuse square, the two quadrilaterals (1 and i) are equal in perimeter and in area. In like manner it may be proved that P and L, E and A, R and G, are equal and similar; and that all are equal to each other in area and in perimeter. The longest side of E is equal and parallel to the longest side of A, which is parallel and equal to the perpendicular plus the smallest side of 2; take then its equivalent the shortest side of 1 from the longest side of E, and there remains the side of the quadrilateral H; which being rectangular with four equal sides is a square equal to the square of the perpendicular of the right-angled triangle.
Consequently the five component parts of the hypothenuse square are equal and similar to and identical with the component parts of the base square together with the square of the perpendicular; proving that the square on the hypothenuse is equivalent in area to the two squares on the base and perpendicular of a right-angled triangle.
The following theorem [discovered in 1835] is also closely allied with the above, it is unnecessary to add the demonstration, as it is quite evident from what has been given before. "Two Squares transformed into One Square. Construction. - Place the two squares side by side, with their bases in a right line: (or one upon the other with their vertical sides in a right line, as in the figure). Bisect the sum of their bases, and the difference of the sides which are vertically in contact. Draw through these points of bisection two lines perpendicular to each other, crossing in the centre, and terminating in the sides of the larger square, which will be thereby divided into four equal parts. Produce these two lines half their length beyond the base and side of the small square, and draw two other lines of equal length perpendicular to them, which will form another square inclosing the small square within four segments equal and similar to the four quarters of the larger of the given squares, and consequently equivalent in area to the two together."
9, North Crescent,
Bedford Square.
(To be continued).
[It will have been noticed that in Mr Perigal's elegant proof of Euclid 1. 47, by dissection and transposition, the PRHI square next four parts into which he has divided the greater side are equal in all respects, so that the division of the squares is symmetrical. In this consists chiefly the elegance of the construction, which is in this respect, I believe, unique, and on the score of simplicity leaves nothing to be desired: in no other proof that I have seen is the division symmetrical, or one square only divided. The dissection forms a very pretty mechanical puzzle; viz. to make a square of the four symmetrical parts, and then another square of the five pieces; as any one will see who will cut out the pieces as in the figure. It is as an amusing and instructive puzzle that Mr Perigal has chiefly circulated his dissection. A very simple proof of Euclid 1. 47 by dissection is given in Todhunter's Euclid, extracted from a paper by De Morgan in Vol. 1. of the Quarterly Journal of Mathematics, and reference is also made there to a work Der Pythagorische Lehrsatz, Mainz. 1821, by J J I Hoffmann, which contains a large number of demonstrations of the theorem. Mr Perigal has twelve or fourteen other proofs, four or five of which are original, and the rest collected; some of these which are not given in Hoffmann, will, I hope, appear in a future number of the Messenger.
J W L Glaisher.]
10. Written 10th April 1888.
EFFECTS OF SINGLE CIRCULAR MOTION, AND OF DOUBLE CIRCULAR MOTION WHEN THE ANGULAR VELOCITIES ARE EQUAL.
When a body turns round a fixed centre or axis, either within itself or at any distance, all its particles move in concentric circles, larger or smaller according to their relative distance from the fixed centre, This is simple circular motion.
In Double circular motion, when the angular velocities are equal in the same direction, - all the particles describe cardioid curves; the different phases varying according to the radial ratio. In Double circular motion, when the angular velocities are equal in contrary directions, - all the particles describe ex-centric circles, which are all of the same size whatever the radial-ratio.
In simply rotating on its own centre or axis, - the body turns its surface to all surrounding objects. In simply revolving round a distant centre, the body also turns its surface to all surrounding objects, but keeps always the same face to the centre of revolution. In double circular motion with equal angular velocities when wired, that is in the same direction, - the body turns round once to the centre of revolution, but twice to surrounding objects. In double circular motion when inverse, that is in contrary directions, with equal angular velocities, - the body turns all its surface in succession to the centre of revolution, but not to objects outside the orbit: because the two inverse movements mutually counteract and neutralise each other; and the body maintains the parallelism of its diameters, producing parallel motion in a circle. Parallel Motion in a Circle, or other Curve, is not a simple or single motion; but compounded of two equal and similar movements in opposite directions, which mutually counteract and neutralise each other's effect of turning round to all points of the compass: the result being a compromise between equal antagonist forces.
H PERIGAL.
10th April 1888
Last Updated March 2021