John F Rigby's publications

John F Rigby wrote many papers and the few we present below are only a very small subset. For some of the papers we give a short extract (often the Abstract), while for others we give an extract from a review. He also wrote one book, with co-author Hidetoshi Fukagawa, about traditional Japanese problems of the 18th and 19th centuries. We give extracts from two reviews of this book.

P Dembowski, Review: Collineations, correlations, polarities, and conics (1967), by J F Rigby, Mathematical Reviews MR0215170 (35 #6013).

In a Pappian projective plane, the definitions of von Staudt and Steiner for a conic are well known to be equivalent if and only if the characteristic of the underlying field is not 2. The paper under review is concerned with an analysis of the difference between the two concepts in the case where the characteristic is 2, and with some related material on projective collineations in arbitrary Pappian planes. Most of the results presented are not new; in fact, the author claims neither completeness nor originality. He says in the introduction: "I shall simply give a few proofs that have occurred to me during the preparation of undergraduate courses in projective geometry." These proofs are all purely synthetic.
M Esser, Review: Axioms for absolute geometry (1968), by J F Rigby, Mathematical Reviews MR0221364 (36 #4416).

The name absolute geometry is given to geometries satisfying all the axioms of order and all the axioms of congruence for Euclidean geometry (but not necessarily the axiom of continuity and the axiom of parallelism). These axioms are found in H G Forder's book [The Foundations of Euclidean geometry, 1927]. The author weakens several of Forder's axioms of congruence, and simplifies several of Forder's proofs. He defines a point $A$ to be isometric to a point $B$ if, for every point $A'$ and for every ray $b$ from $B$ , there exists a point $B'$ on $b$ such that $AA' = BB'$ . While Forder postulated every two points are isometric, the author postulates only that each point is isometric to itself. Other postulates (not of the existence type) must be slightly modified. The author proves that non-isometric points may exist in one-dimensional geometry, but not in higher-dimensional geometry. Forder showed in 1948 that his former axiom C5 on congruent triangles may be replaced by four special cases. Now the author shows that only two of these special cases are needed, and that even these two cases can be further specialised. Also he studies the construction of perpendiculars and of midpoints by weak methods, and gives a simplified proof of the transversal theorem.
I Pieper-Seier, Review: One-dimensional absolute geometries (1970), by J F Rigby, Mathematical reviews MR0365337 (51 #1590).

The author presents axioms for absolute geometries based on incidence, order and congruence and investigates them in particular for the case of dimension one - absolute lines. Two points A, B are said to be isometric if the distance to any circle with centre A is the distance to some circle with centre B. This notion allows one to divide the points of an absolute line into isometry classes. The author constructs in an evident way examples for every finite number of isometry classes. One of these is used to verify that if AB and BC have midpoints then AC also has a mid-point. This requires a two-dimensional proof. If it is assumed that every two isometric points of an absolute line have a midpoint (the line is then called centrally complete), the set of isometry classes forms an elementary Abelian group. A line is said to be normal if a segment cannot be properly contained in an equal segment. Two sufficient conditions for a line to be normal are presented.

The main results for normal lines are: A normal not centrally complete absolute line l can be interpreted as a sub-line of a centrally complete line l' such that no point of l is isometric to any point outside of l. A normal centrally complete line l allows an extended definition of congruence so as to convert l into a line with just one isometry class. In this case the lengths of segments form an ordered Abelian group $G_{l}$ and the group of isometry classes of l is an epimorphic image of $G_{l}$ .

These results are used for the construction of normal centrally complete absolute lines.
J F Rigby, A method of obtaining related triangle inequalities, with applications, Publikacije Elektrotehničkog fakulteta. Serija Matematika i fizika 412/460 (1973), 217-226.

We shall consider a method of connecting inequalities for triplets of positive numbers with inequalities for the sides and angles of triangles and the sides and angles of acute triangles. The method, which involves the use of various substitutions, is described in section 1. These substitutions are not new, but only those given in (ii) and (iii) of section 1 seem to be used with any regularity. In the rest of the paper we shall use the method to connect together various inequalities that are already known, and to prove some new ones.
J F Rigby and James Wiegold, Independent Axioms for Vector Spaces, The Mathematical Gazette 57 (399) (1973), 56-62.

In a recent paper ['Reducing classical axioms', The Mathematical Gazette 60 (1971), 38-40], Victor Bryant shows how the number of axioms required to define a vector space can be reduced to seven (in addition to closure requirements). The main result of his article is that commutativity of addition can be deduced from the other axioms. In the present article we show how to reduce this number to six. For certain underlying fields one or more of these axioms can be deduced from the others. However, the six axioms are in general independent; we invite interested readers to show this by constructing their own counter-examples, which the editor of the Gazette will be pleased to receive.

The authors do not claim originality for all the proofs; those of theorems 1 and 2, for instance, employ standard techniques.

In an article such as this, dealing with the axiomatic basis of a subject it is useful to emphasise that certain operations are distinct by using different symbols to denote them. Addition in a vector space is not usually the same thing as addition in the underlying field, nor is multiplication of a vector by a scalar usually the same thing as multiplication of two scalars; hence we use the slightly unfamiliar notation given below. Some such notation is not only useful but necessary when we come to construct counter-examples; this will be seen later in the article.
J F Rigby, Sextic inequalities for the sides of a triangle, Publikacije Elektrotehničkog fakulteta. Serija Matematika i fizika 498/541 (1975), 51-58.

Many of the interesting inequalities connecting the sides, angles, radii etc. of a triangle, such as can be found in [O Bottema, R Z Dorbevic, R R Janic, D S Mitrinovic and P M Vasic, Geometric Inequalities (Groningen, 1969)] and elsewhere, can be reduced by well known formulae to symmetric homogeneous polynomial inequalities the sides $a , b, c$ of the triangle. Symmetric homogeneous cubic inequalities been completely investigated, and quartic inequalities partially investigated.
J F Rigby, Adventitious Quadrangles: A Geometrical Approach, The Mathematical Gazette 62 (421) (1978), 183-191.

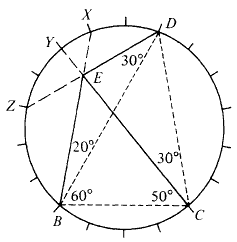
A quadrangle has four vertices, of which no three are collinear, and six sides joining the vertices in pairs. If the angle between each pair of six sides is an integral multiple of $\large\frac{\pi}{n}\normalsize$ radians, $n$ being an integer, the quadrangle is said to be $n$ -adventitious. A quadrangle is adventitious if it is $n$ -adventitious for some $n$ . For example, the quadrangle BCDE on the right (the original adventitious quadrangle from which all the discussion started) is 18-adventitious.

Various problems are posed; in a suitably generalised form these problems can be summarised as: find all adventitious quadrangles and prove their existence by elementary geometry.
S Marcus, Review: Butterflies and snakes (1986), by J F Rigby, Mathematical Reviews MR0891662 (89m:00011).

Rigby observes that in "Butterflies" Escher apparently tries to conceal the systematic framework on which the design is based; but the manner in which the drawing is coloured reveals clearly an underlying framework of circles that must intersect at right angles.
J F Rigby, Equilateral Triangles and the Golden Ratio, The Mathematical Gazette 72 (459) (1988), 27-30.

This article could be subtitled 'Thoughts on contemplating a model tetrahedra inscribed in a dodecahedron'; it is an attempt to communicate pleasure that ensues when logical reasoning is combined with a visual in geometrical figure.
J F Rigby, Some New Regular Compound Tessellations, Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 422 (1863) (1989), 311-318.

When is a compound tessellation regular? H S M Coxeter and N W Johnson have given lists of compound tessellations using two different definitions of regularity, but some compounds missing from these lists are described in the present paper.
J M Wills, Review: Napoleon revisited (1988), by J F Rigby, Mathematical Reviews MR0963992 (89h:51032).

The following result on plane geometry is attributed to Napoleon Bonaparte:
If equilateral triangles are erected externally or internally on the sides of any triangle, then their centres form an equilateral triangle.
The author gives a new proof by using a tessellation of the plane.
J F Rigby, Symmetry in geometry: a personal view, Symmetry Culture and Science 1 (1) (1990), 63-76.

"Symmetry" is a noun used to describe a state or property possessed by certain patterns, objects and geometrical figures. If a plane figure is symmetrical about a line of symmetry or mirror line, then the transformation known as reflection in that line is called a symmetry of the figure. We thus have a different but related use of the word "symmetry", to describe a transformation that maps a figure to itself. There are other well known types of symmetry. The badge or symbol of the Isle of Man is mapped to itself by a rotation through 360/3 degrees, so this rotation is a symmetry of the badge, a three-fold rotational symmetry. A frieze pattern (a pattern that repeats regularly in one direction) has a translation as its fundamental symmetry. These three types of symmetry all preserve lengths and angles: they map any figure to a congruent figure. Because the human eye regards congruent figures (the two wings of a butterfly; the three legs of the Isle of Man badge) as being in some sense "the same", these basic types of symmetry are easily recognised; we shall discuss more subtle forms of symmetry later.

It is not surprising that, in geometry, if we start with a symmetrical situation or figure, we can deduce further symmetrical properties of that figure. Once we have progressed beyond the stage of Euclid's "pons asinorum" (if a triangle has two congruent sides then it has two congruent angles), such deductions of symmetrical properties become almost second nature and are often made instinctively. More surprising are the unexpected occurrences of symmetry. As a simple example, the curves known as conic sections were first defined as sections or slices of a right circular cone, as their name implies. When we obtain an ellipse by taking an oblique plane section of a right circular cone, it is not difficult to see that the complete three-dimensional figure has a plane of symmetry, and hence an ellipse has one line of symmetry; but we could be forgiven for guessing that an ellipse might be more pointed at one end like a bird's egg. The well known fact that an ellipse has two perpendicular lines of symmetry comes as a surprise.
J F Rigby, Compound Tilings and Perfect Colourings, Leonardo 24 (1) (1991), 53-62.

This article is mainly concerned with visual mathematics: the delight of regular colourings of patterns and the way in shapes (some of them strange) fit together. A regular tiling, such as the tiling of squares or of equilateral triangles, is made up of regular shapes fitting together in a regular way. It is sometimes possible to combine a number of regular tilings to make a regular compound tiling: imagine the tilings draw on transparent sheets and laid on top of each other. There is a close connection between regular compound tilings and tilings in which the tiles are coloured to form an orderly, regular pattern. But regularly coloured tilings, usually called perfect colourings, are not always associated with regular compounds in the normal sense. The author's discussion of the surroundings of the hyperbolic plane encourages the reader to contemplate tilings made up of tiles that are not regular, or made up of tiles that are regular but infinite and much more complex than the regular polygons of elementary geometry.
J F Rigby, Napoleon, Escher, and Tessellations, Mathematics Magazine 64 (4) (1991), 242-246.

Napoleon and Escher both have theorems about triangles named after them. It is doubtful whether Napoleon knew enough geometry to prove Napoleon's theorem, and Escher apparently never found a proof for the last part of Escher's theorem. The first part of Escher's theorem is a form of converse of Napoleon's theorem, and both theorems can be proved using tessellations, a method that surely would have appealed to Escher with his love of filling the plane with congruent shapes.
J F Rigby, Traditional Japanese Geometry, Mathematical Melody (September 1997), 40-45.

In the opening paragraph of their book Japanese Temple Geometry Problems [1], H Fukagawa and D Pedoe write "During the greater part of the Edo period (1603-1867) Japan was almost completely cut off from the western world. Books on mathematics, if they entered Japan at all, must have been scarce, and yet, during this long period of isolation people of all social classes, from farmers to samurai, produced theorems in Euclidean geometry which are remarkably different from those produced in the West during the centuries of schism, and sometimes predated these theorems by many years."

As far as I know, [1] is the only extensive publication in English on the subject of Japanese geometry, and this book and the many books on the subject in Japanese consist mainly of collections of problems, with or without solutions. Therefore there are many questions to which I still do not know the answers. How much Western mathematics came to Japan before 1600, from where, and in what form? Did the Japanese have books of mathematical theory and techniques? The authors of [1] say that there were few colleges or universities in Japan during the period in question, but many private schools.

The problems, mainly geometrical, were either published in books or painted on wooden tablets containing text and coloured figures and hung in shrines and temples; hence the use of the term "temple geometry" (a term not used in Japan) although twice as many tablets appear in shrines as in temples. The word for Japanese mathematics is wasan, and the tablets are called sangaku. Collections of sangaku problems, with solutions, appeared in Japanese books in the 18th and 19th centuries, and there are modern books of collections of old problems.

It is my impression that this Japanese geometry differs from Western geometry mainly in the type of problem that seems to have interested and intrigued the Japanese geometers. The Japanese love of artistic design is evident in many of the figures.

Much of my information about the subject has been gained from Hiroshi Okumura, an associate professor at the Maebashi College of Technology, in Gunma Prefecture. We correspond regularly and have discussions at conferences. A few years ago he gave me a copy of The Sangaku in Cunma, published in 1987 by the Gunma Wasan Study Association of which he is a member. This book is a limited edition, beautifully printed, bound and illustrated. It is sometimes possible to understand a problem from its illustration without being able to read the Japanese text.

The text of wasan was usually written in Kanbun, which is based on Chinese (since the Japanese language was written mainly in Chinese characters, I presume this means that Kanbun uses Chinese, rather than Japanese, grammar and syntax). Kanbun cannot be read by most people in modern Japan.

Many of the books on wasan, including [1] are like sets of "Miscellaneous Exercises" at the end of a geometry textbook, but with the rest of the textbook missing. I propose here to give a few examples of such exercises of varying degrees of difficulty, to provide a flavour of the types of problem encountered in wasan. I am not giving solutions here, but my comments may be helpful. Some of the problems have been used in secondary school mathematics clubs, or have provided problems or articles in pedagogical journals.
R Kenyon, Review: Precise colourings of regular triangular tilings (1998), by J F Rigby, Mathematical Reviews MR1601807 (98k:52049).

The article deals with colourings of tilings of the hyperbolic plane with regular triangles. Let {3, n} denote the tiling of the hyperbolic plane with regular (equilateral) triangles meeting n to a vertex (n > 6). A colouring of {3, n} is a choice of colour, among n different colours, for each tile. A colouring is called precise if at each vertex in the tiling each of the n colours appears. A colouring is chirally perfect if each orientation-preserving automorphism of the tiling permutes the colours. A colouring is fully perfect if each automorphism (orientation preserving or not) of the tiling permutes the colours. In this article it is shown how to construct (fully or chirally) perfect, precise colourings of {3, n} for each n.
E Hertel, Review: A double tiling of triangles and regular hexagons (2000), by H Okumura and J F Rigby, Mathematical Reviews MR1758064 (2001j:52028).

The authors consider a special figure consisting of a regular hexagon (erected on a side of a triangle) surrounded by six others and filling triangles. Repeating the construction of such rings by a somewhat unclear rule gives rise to a tiling in the plane by alternate regular hexagons and triangles of topological type of the Archimedean tiling (3,6,3,6). But, in general, this tiling fails to fit together to form a complete tiling of the entire plane. The authors prove that if the tiling is continued around a so-called focal point in a second layer, it joins up with itself to a "double tiling'' of the plane. The proof uses properties of Fermat points and isodynamic points of triangles, which is to be expected. In the last section the authors construct these double tilings by application of a special transformation of the complex plane to the above Archimedean tiling.
J F Rigby, A Turkish interlacing pattern and the olden ratio, Mathematics in School (January 2005), 16-24.

The main topic of this article is an elaborate interlacing pattern on a wall in the Karatay Medrese in Konya, Turkey: how and why do the elements of the pattern fit together, what are the precise measurements of the tiles that make up the pattern, and how might a 13th century Seljuk craftsman have adapted the pattern to produce something less complicated. This main topic is interlaced with accounts of mathematical events in my life during my stay in Turkey more than thirty years ago.

Events in Turkey, Mainly Mathematical

I spent the academic year 1972-73 at Hacettepe University in Ankara, Turkey, as a 'foreign expert'. The name, pronounced 'Hadjet tépé', means Necessity Hill, which sounds like a topographical difficulty encountered in The Pilgrim's Progress. Whilst I was at Hacettepe I gave lecture courses in English on group theory and projective geometry.

I wrote letters to my parents from Ankara at least once a week. My mother kept them all, so I have interspersed this article with a few relevant quotations concerning mathematics or numbers. Even at the British Embassy Church I found mathematical connections.
27 September 1972. The chaplain [Stephen Skemp] is Archdeacon of the Aegean in the Diocese of Gibraltar, and his brother has written a book on 'The Psychology of Learning Mathematics' (Skemp, 1971), which I have partly read.
A friend and colleague at Hacettepe University, Seyfettin Aydin, lent me a fascinating book, Exercices de Géométrie by Frère Gabriel-Marie, from which I learnt about Kiepert's hyperbola and other matters; I wrote about this in the Mathematical Gazette thirty years ago (Rigby, 1973). He also planned a visit to the ancient city of Konya in December 1972, so that we could see the whirling dervishes, and he arranged for me to give a lecture there in April 1973, at a conference on geometry at the Teacher Training College where a friend of his was Principal.

The dervishes of Konya, with their long white full-skirted robes and tall white almost-cylindrical hats, carry out their whirling ceremonies not in the old mosque but in a large 16 sports hall with the inevitable basketball markings on the floor, in order to accommodate the large number of spectators and tourists. The performers belong to the Religious Order of Mevlevi. 'The conical hats represent their tombstones, their coats their tombs, and their skirts their shrouds.'

On my second visit to Konya, the geometry 'konferans' turned out to be just me giving a lecture. I had planned a technical talk for a few mathematics students, on axioms for Euclidean and hyperbolic geometry, with my friend Seyfettin Bey giving a simultaneous translation. But we were shown into the main hall of the college, and my memory tells me that we were confronted with the Principal and all the academic staff in the front row, and the entire student body - it looked like several hundred at first sight - stretching into the distance as far as the eye could see! Somehow I survived the next hour by reshaping the talk as I went along, to suit the unexpected audience; my letter home shows that I must have pitched it right for at least some of them.
6 April 1973. There were about 200 students, all training to be maths or science teachers, and the audience clapped when I wrote some Turkish words on the pocket-handkerchief-sized blackboard. There were a number of questions at the end, which shows that they must have grasped something of what I was saying. ... I think I shall be both singing in and conducting a quartet on Easter morning! So many of the singers will be away on holiday.
An Interlacing Pattern in Konya

After the lecture I remained in Konya for two more days to study some of its famous architecture, especially the tiling patterns on the walls of mosques and other buildings. I was particularly intrigued by an interlacing pattern on the walls of a hall in the Karatay Medrese, a former Islamic theological college built in 1251, now a museum of tiles; the pattern is one of the most complicated that I have come across either in reality or in a photograph or drawing.

Islamic interlacing patterns consist of interlacing braids or ribbons weaving alternately under and over each other; they occur throughout the Muslim world from India to Morocco and Southern Spain, in woodwork or stonework, and in books, but frequently on tiled walls. I am interested in Islamic patterns from a geometrical and artistic viewpoint; for an account of their spiritual significance see, for instance, Critchlow (1976). In the Karatay pattern the braids are black or very dark blue, against a turquoise blue background, with a thin line of white plaster between the black and turquoise tiles; but colour preferences vary between countries. In Spain, for instance, it seems much more common to have white braiding against a multicoloured background. Escher copied some Spanish patterns (Schattschneider, 1990), and they can also be found in guidebooks to Granada and Seville. Other examples of the same type of colouring occur on the front covers of Critchlow (1976) and Bourgoin (1971).
V V Pambuccian, Review: Traditional Japanese mathematics: Problems of the 18th and 19th centuries (2002), by Hidetoshi Fukagawa and John F Rigby, Mathematical Reviews MR2005730 (2004h:01010).

This is a collection of problems written on wooden tablets during the 18th and 19th centuries in Japan, a time when Japan was in its Edo period, in self-imposed isolation from the outer world in order to avoid war with other countries.

It is of great interest both historically, by presenting a native version of geometry, which developed independently of its European counterpart, and as a sourcebook of problems on circles, ellipses, and spheres (these being the main themes that fascinated the mathematicians of those times).

The book consists of two parts. The first part contains the statements of the problems (a small number from number theory, numerical analysis, and the geometry of polygons, a large number from the geometry of circles, of triangles and circles, of ellipses, and from solid geometry, together with a sizeable number of geometric maxima and minima problems). The second part contains solutions to most problems, sometimes the original (Edo period) solution, at other times a modern solution, in case the original one was not found or is unnecessarily complicated.
A R Pargeter, Review: Traditional Japanese mathematics: Problems of the 18th and 19th centuries, by Hidetoshi Fukagawa and John F Rigby, The Mathematical Gazette 88 (511) (2004), 170-171.

From 1603 to 1867, known as the Edo period, Japan isolated itself from the West, so that Japanese mathematics developed on its own lines, without access to techniques and concepts of the rest of the world, but nevertheless to a remarkable degree of complexity. All children were taught to use the soroban (the Japanese abacus), with which remarkably complex calculations can be carried out - the abacus is indeed a digital calculator which is extremely fast and efficient in the hands of an expert. ... It became the custom to inscribe mathematical problems on wooden tablets which were suspended in shrines and temples - simpler and cheaper than publishing a book, we are told! - and this resulted in the wide popularisation of mathematical problem solving. In the course of time some of the tablets disappeared, but the contents of many have been recorded, and there are 879 still surviving.

In Part I, Problems, each chapter begins with 'Fundamental concepts and theorems', followed by a worked example, then a set of problems on the topic of the chapter. In Part 2 are the solutions, many of them 'original', i.e. by mathematicians of the Edo Period, uninfluenced by Western mathematics. Modern solutions are printed where the original solution is very complicated, or is not available: 'readers may enjoy finding simpler solutions to some of the problems'. The modern solutions often involve methods (e.g. inversion), concepts and notations that were not known to the Japanese solvers. The contents of the chapters are, with selected samples of topics: Number theory (Diophantine equations of degrees 1, 2, 3; Chinese remainder theorem); Numerical analysis (Bernoulli numbers, π, Horner's and Newton's methods); Geometry of circles (1, 2, 3, ... up to 10 circles, and beyond! - both alone and with triangles and polygons); Geometry of circles and triangles (and various quadrilaterals); Geometry of ellipses (circles and ellipses in contact, ellipses with triangles and quadrilaterals); Solid geometry (spheres, ellipsoids, cylinders, and cones, variously intersecting); Maxima and minima (mainly in a geometrical context). As will be gathered, the bias of the book is highly geometrical - I should say 90%. There is such a wealth and variety of problems that it is difficult to convey the full flavour of the book. The geometrical problems are all provided with excellent figures, but many of then may seem artificial in that they involve such extraordinary conglomerations of circles and ellipses. None of them is trivial. The solutions, although set out quite fully call for close study, details often having to be filled in by the reader.
...
The appeal of such a book as this is bound to be limited, but if it is your cup of tea you will obtain much fun from it. Sadly the price may mean that many will feel that it is out of their reach, and it is not really a book to be recommended for school - or even college - libraries; so you may just have to save up, or drop hints at Christmas. But it is good value, in the sense that if you enjoy tussling with tough problems on pre-twentieth century subject matter (no 'Modern mathematics' here!) you will not be disappointed.

Last Updated July 2022