Geoffrey C Shephard's publications
MathsSciNet lists around 150 publications for Geoffrey C Shephard so the examples of 11 of his publications we give information on below represents a very small part of his work.
For information about his book Tilings and Patterns co-authored with Branko Grünbaum see 3., 4. and 7. at THIS LINK.
For information about his book Tilings and Patterns co-authored with Branko Grünbaum see 3., 4. and 7. at THIS LINK.
1. Vector Spaces of Finite Dimension (1966), by Geoffrey C Shephard.
1.1 From the Preface.
This book is based on a course of lectures on linear algebra given to second-year Honours students in the University of Birmingham.
A familiarity with the most elementary parts of abstract algebra, together with the properties of matrices and determinants, is assumed. These are summarised briefly in the introductory section, after which the first five chapters give a concise account of the theory of finite-dimensional vector spaces without the use of matrices. In Chapter VI, matrices are introduced, and the methods already developed are applied to them. Most of the notations and terminology used are standard. We have borrowed the notation <> from quantum theory for the inner product of two vectors (Chapter V) and in Chapter II we have introduced a new term, implicit rank, for a quantity which plays an important role in the reduction of linear transformations, but does not seem to have previously been named. Over 150 exercises are included in the text.
1.2. Review by: W H Cockcroft.
The Mathematical Gazette 51 (376) (1967), 177-178.
The author adds to the well-known mathematics series, University Mathematical Texts, a standard work based on lectures given to second year Honours students in his University. He assumes a knowledge of the most elementary parts of abstract algebra including the properties of matrices and determinants, although there is a brief summary, at the beginning of the book, dealing with these matters.
...
There are a fair number of exercises to which solutions are given; the presentation is good, and the above list of topics indicates by its order the general emphasis on "transformations" rather than "matrices".
1.3. Review by: R F Rinehart.
Mathematical Reviews MR0222096 (36 #5148).
Distinguishing features of this compact and abstract treatment of the basic elements of linear algebra are chapters on duality and on the elements of multilinear algebra. ... The book contains about 150 exercises, which vary in difficulty from relatively simple questions to substantive matters customarily included as textual material. The book would seem to be most suitable as a text for a one-semester course for mathematically relatively mature juniors or seniors.
2. Convex polytopes and the upper bound conjecture (1971), by Peter McMullen and Geoffrey C Shephard.
This book is based on a course of lectures on linear algebra given to second-year Honours students in the University of Birmingham.
A familiarity with the most elementary parts of abstract algebra, together with the properties of matrices and determinants, is assumed. These are summarised briefly in the introductory section, after which the first five chapters give a concise account of the theory of finite-dimensional vector spaces without the use of matrices. In Chapter VI, matrices are introduced, and the methods already developed are applied to them. Most of the notations and terminology used are standard. We have borrowed the notation <> from quantum theory for the inner product of two vectors (Chapter V) and in Chapter II we have introduced a new term, implicit rank, for a quantity which plays an important role in the reduction of linear transformations, but does not seem to have previously been named. Over 150 exercises are included in the text.
1.2. Review by: W H Cockcroft.
The Mathematical Gazette 51 (376) (1967), 177-178.
The author adds to the well-known mathematics series, University Mathematical Texts, a standard work based on lectures given to second year Honours students in his University. He assumes a knowledge of the most elementary parts of abstract algebra including the properties of matrices and determinants, although there is a brief summary, at the beginning of the book, dealing with these matters.
...
There are a fair number of exercises to which solutions are given; the presentation is good, and the above list of topics indicates by its order the general emphasis on "transformations" rather than "matrices".
1.3. Review by: R F Rinehart.
Mathematical Reviews MR0222096 (36 #5148).
Distinguishing features of this compact and abstract treatment of the basic elements of linear algebra are chapters on duality and on the elements of multilinear algebra. ... The book contains about 150 exercises, which vary in difficulty from relatively simple questions to substantive matters customarily included as textual material. The book would seem to be most suitable as a text for a one-semester course for mathematically relatively mature juniors or seniors.
2.1. From the Publisher.
Polytopes are the analogues, in higher dimensions, of polygons in the plane and polyhedra in three-dimensional space. Though the study of convex polytopes is one of the oldest branches of mathematics, a surprising number of results and techniques are very recent. In particular, during the last few years there has been a marked revival of interest in combinatorial problems concerning polytopes.
This volume provides an introduction to the theory and covers all the basic results. The final chapter is devoted to a discussion of a classical combinatorial problem, namely the proof of the upper bound conjecture. It includes a survey of all known results in this area.
2.2. Review by: H S M Coxeter.
Mathematical Reviews MR0301635 (46 #791).
This carefully composed book summarises and extends some of the most important parts of B Grünbaum's treatise Convex polytopes (1967). It is a more readable exposition, and brings the subject up to date. It begins with definitions for the various kinds of dependence - linear, affine and convex - in Euclidean -space. A convex polytope is defined as the convex hull of a finite set of points. After proving Carathéodory's theorem, the authors deduce that every polytope is a finite union of simplexes. After defining a polyhedral set as the intersection of a finite number of closed half-spaces, they prove that every convex polytope is a bounded polyhedral set, and that every bounded polyhedral set is a polytope.
3. Additive Frieze Patterns and Multiplication Tables (1976), by Geoffrey C Shephard.
Polytopes are the analogues, in higher dimensions, of polygons in the plane and polyhedra in three-dimensional space. Though the study of convex polytopes is one of the oldest branches of mathematics, a surprising number of results and techniques are very recent. In particular, during the last few years there has been a marked revival of interest in combinatorial problems concerning polytopes.
This volume provides an introduction to the theory and covers all the basic results. The final chapter is devoted to a discussion of a classical combinatorial problem, namely the proof of the upper bound conjecture. It includes a survey of all known results in this area.
2.2. Review by: H S M Coxeter.
Mathematical Reviews MR0301635 (46 #791).
This carefully composed book summarises and extends some of the most important parts of B Grünbaum's treatise Convex polytopes (1967). It is a more readable exposition, and brings the subject up to date. It begins with definitions for the various kinds of dependence - linear, affine and convex - in Euclidean -space. A convex polytope is defined as the convex hull of a finite set of points. After proving Carathéodory's theorem, the authors deduce that every polytope is a finite union of simplexes. After defining a polyhedral set as the intersection of a finite number of closed half-spaces, they prove that every convex polytope is a bounded polyhedral set, and that every bounded polyhedral set is a polytope.
3.1. From the text.
Geoffrey C Shephard, Additive Frieze Patterns and Multiplication Tables, The Mathematical Gazette 60 (413) (1976), 178-184.
A frieze pattern is an array of numbers arranged in staggered rows, like the bricks in a wall. In the case of a multiplicative frieze pattern the top and bottom rows consist entirely of ones, and for each 'diamond' of four elements
b
a d
c
the unimodular rule
holds. These frieze patterns have many curious properties, and for further details the reader is referred to the article Triangulated polygons and frieze patterns by J H Conway and H S M Coxeter which appeared in The Mathematical Gazette 57 (1973). This paper gives an excellent bibliography of frieze patterns and related topics. We now mention two of these properties ...
...

The purpose of this paper is to describe a new type of pattern which we shall call an additive frieze pattern. This has properties just as remarkable as those of a multiplicative pattern. Here again we have an array of numbers in staggered rows, but the top and bottom rows consist entirely of zeros. Instead of the unimodular rule we have the additive relation
for each diamond of four elements.
4. The Mathematics of a Mechanical Puzzle (1977), by Geoffrey C Shephard.
Geoffrey C Shephard, Additive Frieze Patterns and Multiplication Tables, The Mathematical Gazette 60 (413) (1976), 178-184.
A frieze pattern is an array of numbers arranged in staggered rows, like the bricks in a wall. In the case of a multiplicative frieze pattern the top and bottom rows consist entirely of ones, and for each 'diamond' of four elements
b
a d
c
the unimodular rule
holds. These frieze patterns have many curious properties, and for further details the reader is referred to the article Triangulated polygons and frieze patterns by J H Conway and H S M Coxeter which appeared in The Mathematical Gazette 57 (1973). This paper gives an excellent bibliography of frieze patterns and related topics. We now mention two of these properties ...
...

The purpose of this paper is to describe a new type of pattern which we shall call an additive frieze pattern. This has properties just as remarkable as those of a multiplicative pattern. Here again we have an array of numbers in staggered rows, but the top and bottom rows consist entirely of zeros. Instead of the unimodular rule we have the additive relation
for each diamond of four elements.
4.1. From the text.
Geoffrey C Shephard, The Mathematics of a Mechanical Puzzle, The Mathematical Gazette 61 (417) (1977), 174-178.
For some mechanical puzzles there exists a complete mathematical analysis. The purpose of this note is to describe one such puzzle, together with a number of variations of it. In the classroom the puzzle could be used as a teaching aid to introduce children to binary notation, mathematical induction, congruences, as well as some of the concepts of group theory. My own ten-year-old son was delighted to find that counting in binary notation, an idea to which he had been introduced in a purely theoretical way, leads to an easy method of solving the puzzle.
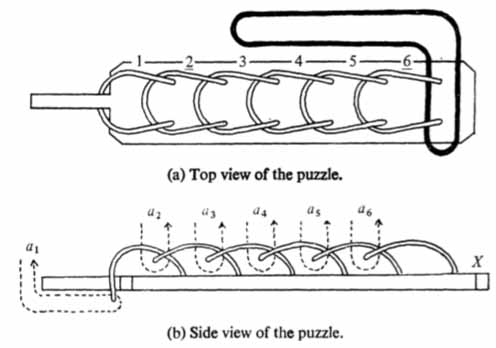
The puzzle is shown on the right. It is available commercially made of wire and plastic, but it is quite simple to make it oneself out of thick string and cardboard or wood. The home-made version has the advantage that one can easily modify it and so experiment with the variants to be described later. Before looking at the next section the reader is urged to make the puzzle and try to solve it for himself - in this way he will soon be convinced that it is by no means trivial.
5. Tilings by Regular Polygons (1977), by Branko Grünbaum and Geoffrey C Shephard.
Geoffrey C Shephard, The Mathematics of a Mechanical Puzzle, The Mathematical Gazette 61 (417) (1977), 174-178.
For some mechanical puzzles there exists a complete mathematical analysis. The purpose of this note is to describe one such puzzle, together with a number of variations of it. In the classroom the puzzle could be used as a teaching aid to introduce children to binary notation, mathematical induction, congruences, as well as some of the concepts of group theory. My own ten-year-old son was delighted to find that counting in binary notation, an idea to which he had been introduced in a purely theoretical way, leads to an easy method of solving the puzzle.

The puzzle is shown on the right. It is available commercially made of wire and plastic, but it is quite simple to make it oneself out of thick string and cardboard or wood. The home-made version has the advantage that one can easily modify it and so experiment with the variants to be described later. Before looking at the next section the reader is urged to make the puzzle and try to solve it for himself - in this way he will soon be convinced that it is by no means trivial.
5.1. From the text.
Branko Grünbaum and Geoffrey C Shephard, Tilings by Regular Polygons, Mathematics Magazine 50 (5) (1977), 227-247.
A tiling of the plane is a family of sets - called tiles - that cover the plane without gaps or overlaps. ("Without overlaps" means that the intersection of any two of the sets has measure (area) zero.) Tilings are also known as tessellations, pavings, or mosaics; they have appeared in human activities since prehistoric times. Their mathematical theory is mostly elementary, but nevertheless it contains a rich supply of interesting and sometimes surprising facts as well as many challenging problems at various levels. The same is true for the special class of tilings that will be discussed here - more or less regular tilings by regular polygons. These types were chosen because they are accessible without any need for lengthy introductions, and also because they were the first to be the subject of mathematical research. The pioneering investigation was done by Johannes Kepler, more than three and a half centuries ago. Additional historical data will be given later ... We shall see that these drawings contain (at least in embryonic form) many aspects of tilings by regular polygons which even at present are not completely developed.
As is the case with many other notions, the concept of "more or less regular" tilings by regular polygons developed through the centuries in response to the interests of various investigators; it is still changing, and no single point of view can claim absolute superiority over all others. Our presentation reflects our preferences, although many other definitions and directions are possible .... For most of our assertions we provide only hints which we hope will be sufficient for interested readers to construct complete proofs.
5.2. Review by H S M Coxeter.
Mathematical Reviews MR0500451 (58 #18090).
The authors begin by reproducing 29 drawings by J Kepler, first published in 1619, of "various more or less regular tilings of the plane by regular polygons." They discuss many reasonable meanings for "more or less regular." One of the most striking is "uniform but not edge-to-edge." Here a vertex of one tile (called a "node" of the tiling) is interior to an edge of another, and the symmetries of the tiling act transitively on the nodes. It is "not hard to prove" that there are just seven one-parameter families of such tilings. In the rest of the paper, tiles meet edge-to-edge, though in the case of star polygons Kepler recognised two ways to define an edge. Sometimes, as in his stellated dodecahedra, he regarded the star pentagon {} as a "pentagram" having five vertices and five edges (which accidentally intersect internally); but sometimes he regarded it as a "pentacle" having ten vertices and ten edges. Taking the latter standpoint, it is "easy to see" that there are just four one-parameter families of uniform tilings that involve -pointed stars having the same symmetries as regular convex -gons. These have a particularly pleasing appearance. In one case the tiling is "reflexible", in the other three it is chiral (occurring in two enantiomorphic forms).
6. Satins and Twills: An Introduction to the Geometry of Fabrics (1980), by Branko Grünbaum and Geoffrey C Shephard.
Branko Grünbaum and Geoffrey C Shephard, Tilings by Regular Polygons, Mathematics Magazine 50 (5) (1977), 227-247.
A tiling of the plane is a family of sets - called tiles - that cover the plane without gaps or overlaps. ("Without overlaps" means that the intersection of any two of the sets has measure (area) zero.) Tilings are also known as tessellations, pavings, or mosaics; they have appeared in human activities since prehistoric times. Their mathematical theory is mostly elementary, but nevertheless it contains a rich supply of interesting and sometimes surprising facts as well as many challenging problems at various levels. The same is true for the special class of tilings that will be discussed here - more or less regular tilings by regular polygons. These types were chosen because they are accessible without any need for lengthy introductions, and also because they were the first to be the subject of mathematical research. The pioneering investigation was done by Johannes Kepler, more than three and a half centuries ago. Additional historical data will be given later ... We shall see that these drawings contain (at least in embryonic form) many aspects of tilings by regular polygons which even at present are not completely developed.
As is the case with many other notions, the concept of "more or less regular" tilings by regular polygons developed through the centuries in response to the interests of various investigators; it is still changing, and no single point of view can claim absolute superiority over all others. Our presentation reflects our preferences, although many other definitions and directions are possible .... For most of our assertions we provide only hints which we hope will be sufficient for interested readers to construct complete proofs.
5.2. Review by H S M Coxeter.
Mathematical Reviews MR0500451 (58 #18090).
The authors begin by reproducing 29 drawings by J Kepler, first published in 1619, of "various more or less regular tilings of the plane by regular polygons." They discuss many reasonable meanings for "more or less regular." One of the most striking is "uniform but not edge-to-edge." Here a vertex of one tile (called a "node" of the tiling) is interior to an edge of another, and the symmetries of the tiling act transitively on the nodes. It is "not hard to prove" that there are just seven one-parameter families of such tilings. In the rest of the paper, tiles meet edge-to-edge, though in the case of star polygons Kepler recognised two ways to define an edge. Sometimes, as in his stellated dodecahedra, he regarded the star pentagon {} as a "pentagram" having five vertices and five edges (which accidentally intersect internally); but sometimes he regarded it as a "pentacle" having ten vertices and ten edges. Taking the latter standpoint, it is "easy to see" that there are just four one-parameter families of uniform tilings that involve -pointed stars having the same symmetries as regular convex -gons. These have a particularly pleasing appearance. In one case the tiling is "reflexible", in the other three it is chiral (occurring in two enantiomorphic forms).
6.1. From the text.
Branko Grünbaum and Geoffrey C Shephard, Satins and Twills: An Introduction to the Geometry of Fabrics, Mathematics Magazine 53 (3) (1980), 139-161.
Weaving is one of the oldest activities of mankind and so it is hardly surprising that there exists a vast literature on the subject. But this literature is almost entirely concerned with the practical aspects of weaving; any treatment of the theoretical problem of designing fabrics with prescribed mathematical properties is conspicuously absent. And this is so in spite of the fact that many fabrics which are mathematically interesting were discovered empirically long ago by practitioners of the weaver's craft. One wonders how geometers can fail to be fascinated by the diagrams of fabrics that abound in the literature. Yet, so far as we are aware, the only papers that attempt to treat fabric design from a mathematical point of view are those of Lucas who published about a century ago, an isolated paper of Shorter which appeared in 1920, and a series of three papers by Woods published in 1935. All three authors were concerned principally with satins (or sateens), a type of fabric which we shall discuss in the third section of this paper.
The "geometry of fabrics", as we shall call it, involves ideas from elementary geometry, group theory, number theory and combinatorics. There is a large number of open problems, to some of which we shall draw attention in the following pages.
In order to make the subject manageable, it will be necessary to idealise the concept of a fabric. For example, we shall always assume that our fabrics are unbounded, that is, that they continue indefinitely in every direction. Thus edge-effects and selvedges (which are of great concern to the practical weaver) will be entirely ignored here. A fabric will consist of "strands" woven together and we shall only discuss those fabrics in which the strands are straight and lie in one of two directions, usually at right-angles to each other. Without these restrictions there are many other possibilities about which extremely little seems to be known.
...
It is clear that the material in this paper is only the beginning of a large subject; generalisations in many directions are possible and most of these are completely unexplored. ...
There is no need to restrict attention to the plane. For example a fabric in the shape of a torus can be constructed from two sets of "annular" strands, or even from just two strands if these are allowed to "spiral" round the torus. Recently Jean J Pedersen has constructed isonemal fabrics on polyhedral surfaces, but there still remain many open problems concerning fabrics on manifolds and other surfaces in three dimensional space. Yet another possibility is to investigate fabrics in which the strands lie in more than two directions. (Practical examples of these occur in basketry.) Some results on such fabrics are already known and will be described in a forthcoming paper by the authors. We can already say that in this case a large number of new isonemal fabrics exists.
6.2. Review by G Ewald.
Mathematical Reviews MR0600071 (82k:52017).
This is a thorough mathematical analysis of weaving, or the geometry of fabrics. Only a few partial results have been found up to now, the last one published in 1935.
First, a mathematical meaning is given to concepts such as strand, fabric, warp, weft, satin, twill, etc. Generating principles are presented (using groups); furthermore, certain types of fabrics are classified. In some cases numbers of possible types of fabrics are given by formulas. ...
Further research is stimulated by discussing open problems.
7. Space Filling with Identical Symmetrical Solids (1985), by Geoffrey C Shephard.
Branko Grünbaum and Geoffrey C Shephard, Satins and Twills: An Introduction to the Geometry of Fabrics, Mathematics Magazine 53 (3) (1980), 139-161.
Weaving is one of the oldest activities of mankind and so it is hardly surprising that there exists a vast literature on the subject. But this literature is almost entirely concerned with the practical aspects of weaving; any treatment of the theoretical problem of designing fabrics with prescribed mathematical properties is conspicuously absent. And this is so in spite of the fact that many fabrics which are mathematically interesting were discovered empirically long ago by practitioners of the weaver's craft. One wonders how geometers can fail to be fascinated by the diagrams of fabrics that abound in the literature. Yet, so far as we are aware, the only papers that attempt to treat fabric design from a mathematical point of view are those of Lucas who published about a century ago, an isolated paper of Shorter which appeared in 1920, and a series of three papers by Woods published in 1935. All three authors were concerned principally with satins (or sateens), a type of fabric which we shall discuss in the third section of this paper.
The "geometry of fabrics", as we shall call it, involves ideas from elementary geometry, group theory, number theory and combinatorics. There is a large number of open problems, to some of which we shall draw attention in the following pages.
In order to make the subject manageable, it will be necessary to idealise the concept of a fabric. For example, we shall always assume that our fabrics are unbounded, that is, that they continue indefinitely in every direction. Thus edge-effects and selvedges (which are of great concern to the practical weaver) will be entirely ignored here. A fabric will consist of "strands" woven together and we shall only discuss those fabrics in which the strands are straight and lie in one of two directions, usually at right-angles to each other. Without these restrictions there are many other possibilities about which extremely little seems to be known.
...
It is clear that the material in this paper is only the beginning of a large subject; generalisations in many directions are possible and most of these are completely unexplored. ...
There is no need to restrict attention to the plane. For example a fabric in the shape of a torus can be constructed from two sets of "annular" strands, or even from just two strands if these are allowed to "spiral" round the torus. Recently Jean J Pedersen has constructed isonemal fabrics on polyhedral surfaces, but there still remain many open problems concerning fabrics on manifolds and other surfaces in three dimensional space. Yet another possibility is to investigate fabrics in which the strands lie in more than two directions. (Practical examples of these occur in basketry.) Some results on such fabrics are already known and will be described in a forthcoming paper by the authors. We can already say that in this case a large number of new isonemal fabrics exists.
6.2. Review by G Ewald.
Mathematical Reviews MR0600071 (82k:52017).
This is a thorough mathematical analysis of weaving, or the geometry of fabrics. Only a few partial results have been found up to now, the last one published in 1935.
First, a mathematical meaning is given to concepts such as strand, fabric, warp, weft, satin, twill, etc. Generating principles are presented (using groups); furthermore, certain types of fabrics are classified. In some cases numbers of possible types of fabrics are given by formulas. ...
Further research is stimulated by discussing open problems.
7.1. From the text.
Geoffrey C Shephard, Space Filling with Identical Symmetrical Solids, The Mathematical Gazette 69 (448) (1985), 117-120.
In his article with the above title (in the June 1984 Gazette) J E Drummond mentions four "symmetrical" solids that fill space, that is tile Euclidean 3-space . He remarks that three of these are well known (the cube, rhombic dodecahedron, and truncated octahedron) but that there is also a fourth (the "tetrahedron with bevelled vertices") of which he has "been unable to find any record". The latter was, in fact, discovered about seventy years ago by Foppl and has since been described in several publications.
At the end of his article Drummond remarks that "it would be interesting to know if these [four solids described above] are the only identical symmetrical space-filling solids". This question does not admit an answer without a more explicit statement as to what is meant by "symmetrical" and by "solids". If the question is taken to concern "convex solids having (at least) the symmetries of the regular tetrahedron", then Drummond's list appears to be complete, although it seems that this has never been proved. (A proof is made more difficult by the fact that there may exist symmetries of the solid which are not symmetries of the tiling. ...
But if the restrictions are weakened, the question has a negative answer. Thus if convexity is waived there are infinitely many different solids with tetrahedral symmetry which not only tile by congruent copies, but are, in fact, "parallelohedra".
...
It seems to us that geometry of this kind described here (concerning polyhedra, space-fillings, symmetry groups, etc.) is both interesting and exciting. It is a tragedy that our present educational system completely ignores these subjects and the little time available for teaching geometry seems to be devoted to comparatively simple and uninteresting topics. Perhaps this is one of the reasons why there still remain so many unsolved geometrical problems in the familiar three-dimensional space in which we live.
8. Interlace Patterns in Islamic and Moorish Art (1992), by Branko Grünbaum and Geoffrey C Shephard.
Geoffrey C Shephard, Space Filling with Identical Symmetrical Solids, The Mathematical Gazette 69 (448) (1985), 117-120.
In his article with the above title (in the June 1984 Gazette) J E Drummond mentions four "symmetrical" solids that fill space, that is tile Euclidean 3-space . He remarks that three of these are well known (the cube, rhombic dodecahedron, and truncated octahedron) but that there is also a fourth (the "tetrahedron with bevelled vertices") of which he has "been unable to find any record". The latter was, in fact, discovered about seventy years ago by Foppl and has since been described in several publications.
At the end of his article Drummond remarks that "it would be interesting to know if these [four solids described above] are the only identical symmetrical space-filling solids". This question does not admit an answer without a more explicit statement as to what is meant by "symmetrical" and by "solids". If the question is taken to concern "convex solids having (at least) the symmetries of the regular tetrahedron", then Drummond's list appears to be complete, although it seems that this has never been proved. (A proof is made more difficult by the fact that there may exist symmetries of the solid which are not symmetries of the tiling. ...
But if the restrictions are weakened, the question has a negative answer. Thus if convexity is waived there are infinitely many different solids with tetrahedral symmetry which not only tile by congruent copies, but are, in fact, "parallelohedra".
...
It seems to us that geometry of this kind described here (concerning polyhedra, space-fillings, symmetry groups, etc.) is both interesting and exciting. It is a tragedy that our present educational system completely ignores these subjects and the little time available for teaching geometry seems to be devoted to comparatively simple and uninteresting topics. Perhaps this is one of the reasons why there still remain so many unsolved geometrical problems in the familiar three-dimensional space in which we live.
8.1. From the text.
Branko Grünbaum and Geoffrey C Shephard, Interlace Patterns in Islamic and Moorish Art, Leonardo 25 (3/4), Visual Mathematics: Special Double Issue (1992), 331-339.
Interlace patterns occur frequently in the ornaments of various cultures, especially in Islamic and Moorish art. By interlace pattern we mean a periodic pattern that appears to consist of interwoven strands. (The exact meaning of the term 'periodic pattern' will be explained later.) The largest published collection of interlace patterns is that of J Bourgoin; more precisely, the majority of Bourgoin's diagrams can be interpreted as representing such patterns, and it appears that they were, in fact, created with interlace patterns as originals. Other examples can be found in works by d'Avennes, El Said and Parman, Wade, and Humbert. A number of authors have relied on the Bourgoin drawings in their research; for example, they have been used by Makovicky and Makovicky in their analysis of the frequencies with which various classes of symmetry groups are represented in Islamic patterns.
This article has three main goals. First, we will observe that most of the interlace patterns shown by Bourgoin consist either of identical (congruent) strands or of two shapes of strands. This is unexpected because in many cases the strand patterns are very complicated - some of them are so intricately interwoven that a repeat is unlikely to have been visible in any actual ornament.
9. Pick's Theorem (1993), by Branko Grünbaum and Geoffrey C Shephard.
Branko Grünbaum and Geoffrey C Shephard, Interlace Patterns in Islamic and Moorish Art, Leonardo 25 (3/4), Visual Mathematics: Special Double Issue (1992), 331-339.
Interlace patterns occur frequently in the ornaments of various cultures, especially in Islamic and Moorish art. By interlace pattern we mean a periodic pattern that appears to consist of interwoven strands. (The exact meaning of the term 'periodic pattern' will be explained later.) The largest published collection of interlace patterns is that of J Bourgoin; more precisely, the majority of Bourgoin's diagrams can be interpreted as representing such patterns, and it appears that they were, in fact, created with interlace patterns as originals. Other examples can be found in works by d'Avennes, El Said and Parman, Wade, and Humbert. A number of authors have relied on the Bourgoin drawings in their research; for example, they have been used by Makovicky and Makovicky in their analysis of the frequencies with which various classes of symmetry groups are represented in Islamic patterns.
This article has three main goals. First, we will observe that most of the interlace patterns shown by Bourgoin consist either of identical (congruent) strands or of two shapes of strands. This is unexpected because in many cases the strand patterns are very complicated - some of them are so intricately interwoven that a repeat is unlikely to have been visible in any actual ornament.
9.1. From the text.
Branko Grünbaum and Geoffrey C Shephard, Pick's Theorem, The American Mathematical Monthly 100 (2) (1993), 150-161.
Some years ago, the Northwest Mathematics Conference was held in Eugene, Oregon. To add a bit of local flavour, a forester was included on the program, and those who attended his session were introduced to a variety of nice examples which illustrated the important role that mathematics plays in the forest industry. One of his problems was concerned with the calculation of the area inside a polygonal region drawn to scale from field data obtained for a stand of timber by a timber cruiser. The standard method is to overlay a scale drawing with a transparency on which a square dot pattern is printed. Except for a factor dependent on the relative sizes of the drawing and the square grid, the area inside the polygon is computed by counting all of the dots fully inside the polygon, and then adding half of the number of dots which fall on the bounding edges of the polygon. Although the speaker was not aware that he was essentially using Pick's formula, I was delighted to see that one of my favourite mathematical results was not only beautiful, but even useful. (From DeTemple [1989].)
The discoverer of the theorem in question, Georg Alexander Pick, was born in 1859 in Vienna, and died around 1943 in the Theresienstadt concentration camp. He made significant contributions to analysis and differential geometry. The theorem we are concerned with was first published in 1899. It became widely known through Steinhaus's delightful book Mathematical Snapshots. Pick's theorem concerns lattice polygons ("geoboard polygons"), that is, polygons with all vertices at points of the square unit lattice . The original form of the theorem concerns simple polygons, whose edges do not cross one another. ...
In this paper we shall extend Pick's theorem to more general lattice polygons, by allowing multiple intersections, and even overlapping, of the edges. We shall make use of results on rotation numbers, winding numbers and tangent numbers of such polygons ; a brief account of the necessary definitions and facts concerning these numbers will be given here, but for more details, examples, and proofs of some of our assertions, the reader should consult [B Grünbaum and G C Shephard, Rotation and winding numbers for polygons and curves, Trans. Amer. Math. Soc. 322 (1990), 169-187].
...
A major difference between our treatment of Pick's Theorem and that of earlier papers is that oriented polygons are used here. If suitable orientations are introduced our main theorem implies all known variants of Pick's Theorem as it relates to plane lattice polygons. It does not, of course, include the three-dimensional version, nor the results concerning the "hexagonal lattice" (which is not a lattice in the usual terminology) or Archimedean tilings.
9.2. Review by: Ren Ding.
Mathematical Reviews MR1212401 (94j:52012).
A polygon with all vertices at points of the square unit lattice L is called a lattice polygon; a polygon is simple if its edges have no mutual intersections other than those of adjacent edges at the common vertices. Pick's theorem asserts that the area of a simple lattice polygon is given by the expression , where is the number of lattice points in the interior of , and is the number of lattice points on the boundary of . In this paper the authors extend Pick's theorem to more general lattice polygons by allowing multiple intersections, and even overlapping, of the edges. In the discussion the authors make extensive use of results on rotation numbers, winding numbers and tangent numbers of such polygons . The definitions and results concerning these numbers are from the authors' important paper Rotation and winding numbers for planar polygons and curves (1990).
10. Interlinked Loops (2006), by Geoffrey C Shephard.
Branko Grünbaum and Geoffrey C Shephard, Pick's Theorem, The American Mathematical Monthly 100 (2) (1993), 150-161.
Some years ago, the Northwest Mathematics Conference was held in Eugene, Oregon. To add a bit of local flavour, a forester was included on the program, and those who attended his session were introduced to a variety of nice examples which illustrated the important role that mathematics plays in the forest industry. One of his problems was concerned with the calculation of the area inside a polygonal region drawn to scale from field data obtained for a stand of timber by a timber cruiser. The standard method is to overlay a scale drawing with a transparency on which a square dot pattern is printed. Except for a factor dependent on the relative sizes of the drawing and the square grid, the area inside the polygon is computed by counting all of the dots fully inside the polygon, and then adding half of the number of dots which fall on the bounding edges of the polygon. Although the speaker was not aware that he was essentially using Pick's formula, I was delighted to see that one of my favourite mathematical results was not only beautiful, but even useful. (From DeTemple [1989].)
The discoverer of the theorem in question, Georg Alexander Pick, was born in 1859 in Vienna, and died around 1943 in the Theresienstadt concentration camp. He made significant contributions to analysis and differential geometry. The theorem we are concerned with was first published in 1899. It became widely known through Steinhaus's delightful book Mathematical Snapshots. Pick's theorem concerns lattice polygons ("geoboard polygons"), that is, polygons with all vertices at points of the square unit lattice . The original form of the theorem concerns simple polygons, whose edges do not cross one another. ...
In this paper we shall extend Pick's theorem to more general lattice polygons, by allowing multiple intersections, and even overlapping, of the edges. We shall make use of results on rotation numbers, winding numbers and tangent numbers of such polygons ; a brief account of the necessary definitions and facts concerning these numbers will be given here, but for more details, examples, and proofs of some of our assertions, the reader should consult [B Grünbaum and G C Shephard, Rotation and winding numbers for polygons and curves, Trans. Amer. Math. Soc. 322 (1990), 169-187].
...
A major difference between our treatment of Pick's Theorem and that of earlier papers is that oriented polygons are used here. If suitable orientations are introduced our main theorem implies all known variants of Pick's Theorem as it relates to plane lattice polygons. It does not, of course, include the three-dimensional version, nor the results concerning the "hexagonal lattice" (which is not a lattice in the usual terminology) or Archimedean tilings.
9.2. Review by: Ren Ding.
Mathematical Reviews MR1212401 (94j:52012).
A polygon with all vertices at points of the square unit lattice L is called a lattice polygon; a polygon is simple if its edges have no mutual intersections other than those of adjacent edges at the common vertices. Pick's theorem asserts that the area of a simple lattice polygon is given by the expression , where is the number of lattice points in the interior of , and is the number of lattice points on the boundary of . In this paper the authors extend Pick's theorem to more general lattice polygons by allowing multiple intersections, and even overlapping, of the edges. In the discussion the authors make extensive use of results on rotation numbers, winding numbers and tangent numbers of such polygons . The definitions and results concerning these numbers are from the authors' important paper Rotation and winding numbers for planar polygons and curves (1990).
10.1. From the text.
Geoffrey C Shephard, Interlinked Loops, The Mathematical Gazette 90 (518) (2006), 249-252.
Many problems in topology are easy to state, but some are extremely difficult to solve. And even if they are easy, they may have surprising solutions. For example, take a tyre inner tube, that is, a toroidal surface with a hole (for the valve!). Can one turn it inside out? The answer is 'yes' but if one actually carries out this procedure the result is entirely unexpected.
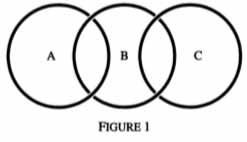
Here we present some problems which are not easy but are quite amusing. To introduce them, consider a chain of three loops A, B and C (see Figure 1). Imagine these are loops of string. Then if we cut loop B and remove it, clearly loops A and C are not linked and so can be separated from each other. But if we cut loop A or loop C, and remove it, the remaining two loops are linked and so cannot be separated. Our first problem is this: How can one arrange the three loops so that, whichever loop you cut and remove, the remaining two loops are linked? Our second problem is to arrange the three loops so that they are interlinked, but whichever loop you cut and remove, the remaining two loops are not linked and so can be separated.
11. A Jigsaw Problem (2009), by Geoffrey C Shephard.
Geoffrey C Shephard, Interlinked Loops, The Mathematical Gazette 90 (518) (2006), 249-252.
Many problems in topology are easy to state, but some are extremely difficult to solve. And even if they are easy, they may have surprising solutions. For example, take a tyre inner tube, that is, a toroidal surface with a hole (for the valve!). Can one turn it inside out? The answer is 'yes' but if one actually carries out this procedure the result is entirely unexpected.

Here we present some problems which are not easy but are quite amusing. To introduce them, consider a chain of three loops A, B and C (see Figure 1). Imagine these are loops of string. Then if we cut loop B and remove it, clearly loops A and C are not linked and so can be separated from each other. But if we cut loop A or loop C, and remove it, the remaining two loops are linked and so cannot be separated. Our first problem is this: How can one arrange the three loops so that, whichever loop you cut and remove, the remaining two loops are linked? Our second problem is to arrange the three loops so that they are interlinked, but whichever loop you cut and remove, the remaining two loops are not linked and so can be separated.
11.1. From the text.
Geoffrey C Shephard, A Jigsaw Problem, The Mathematical Gazette 93 (526) (2009), 58-65.
Recently, when solving a jigsaw puzzle, I noticed that many of the pieces were symmetric in some sense; they had either reflective or rotational symmetry. This made me wonder if it was possible for all the pieces in a puzzle to be different shapes, and yet have some prescribed symmetry.
Let us begin by formulating this as a mathematical problem. First recall the notations for the symmetry groups of a plane (bounded) figure. Clearly each symmetry must leave at least one point fixed (for example, the centroid) and we shall refer to any such point as a centre. For any positive integer there are two groups: the rotation group of order which, for , comprises rotations about the centre through angles which are multiples of . (For , conventionally, is the trivial group consisting of the identity element alone.) For , a figure has symmetry group if, and only if, it is centrally symmetric. The other group is the reflection group of order . This comprises reflections in lines which pass through the centre that make angles with each other which are multiples of together with the rotations of . The group contains only one reflection and has just two elements.
For simplicity, we think of the completed puzzle as being a convex polygon. So our problem can be formulated thus:
Given any one of the groups or , is it possible to dissect a given convex polygon (the base polygon) into at least two connected and simply-connected pieces (tiles) all of which have this same prescribed symmetry group?
Geoffrey C Shephard, A Jigsaw Problem, The Mathematical Gazette 93 (526) (2009), 58-65.
Recently, when solving a jigsaw puzzle, I noticed that many of the pieces were symmetric in some sense; they had either reflective or rotational symmetry. This made me wonder if it was possible for all the pieces in a puzzle to be different shapes, and yet have some prescribed symmetry.
Let us begin by formulating this as a mathematical problem. First recall the notations for the symmetry groups of a plane (bounded) figure. Clearly each symmetry must leave at least one point fixed (for example, the centroid) and we shall refer to any such point as a centre. For any positive integer there are two groups: the rotation group of order which, for , comprises rotations about the centre through angles which are multiples of . (For , conventionally, is the trivial group consisting of the identity element alone.) For , a figure has symmetry group if, and only if, it is centrally symmetric. The other group is the reflection group of order . This comprises reflections in lines which pass through the centre that make angles with each other which are multiples of together with the rotations of . The group contains only one reflection and has just two elements.
For simplicity, we think of the completed puzzle as being a convex polygon. So our problem can be formulated thus:
Given any one of the groups or , is it possible to dissect a given convex polygon (the base polygon) into at least two connected and simply-connected pieces (tiles) all of which have this same prescribed symmetry group?
Last Updated February 2023