An elementary approach to concepts by Yakov G Sinai
Arne B Sletsjøe wrote four elementary articles which illustrate ideas introduced by Yakov Sinai. These articles are: Chaos; Dynamical billiard; Entropy of 0, 1-sequences; and The entropy of a dynamical system. These are to be found at
https://abelprize.no/abel-prize-laureates/2014
Below we give extracts from these articles.
Click on a link below to go to that article
https://abelprize.no/abel-prize-laureates/2014
Below we give extracts from these articles.
Click on a link below to go to that article
1. Chaos.
Chaos as a phenomenon of daily life is something everybody has experienced. For mathematicians it has been important to understand the deeper meaning of this concept, and how to quantify chaotic behaviour.
The term chaos has its origin from the Greek term χάος and has been interpreted as "a moving, formless mass from which the cosmos and the gods originated." A more up-to-date definition of the term is something like a state of complete confusion and disorder, with no immediate view of achieving stability.
We have at least two kinds of chaos. A random system will in many cases appear to us as chaotic. Throwing a dice may result in a sequence 3, 1, 5, 3, 3, 2, 6, 1, ... , for which we are sure to find no pattern. Total unpredictability is often considered as chaos.
Another kind of chaos is what is denoted deterministic chaos. Deterministic is more or less synonymous with predictable, and deterministic chaos may therefore seem to be somewhat paradoxical. But the chaotic behaviour stems from the fact that the system is sensitively dependent on its initial state. As an example, consider the following set-up. Onto a rather big sphere we drop small spheres, always trying to hit the top of the bigger sphere. The smaller spheres jump or roll in different directions, depending on which side of the top point they land. The chaotic behaviour is a result of small differences in the initial state, i.e. the landing point. This is a deterministic chaotic situation, deterministic because the smaller spheres just obey the physical laws of motion, and chaotic because of the sensitive initial state dependency.
Another example of deterministic chaos is the three-body problem. This problem concerns the trajectories of three bodies, which mutually influence each others' motion, due to gravitational forces. The system is deterministic because every single movement can be predicted using the physical laws of motion, and it is chaotic because of its sensitive dependency on the initial state. This dependency is often denoted the butterfly effect, referring to the theoretical example of a hurricane's formation being contingent on whether or not a distant butterfly has flapped its wings several weeks earlier.
Even the apparently random like system of throwing dice is in fact deterministic. Fixing the initial position and velocity of the dice, the precise shape of the dice and taking into account our accurate knowledge of the surface of the table, we are able to predict the result of a throw of a dice, at least theoretically. But if we impose a small change in an input parameter, we are lost. So even if the system is deterministic, it appears to us as being stochastic.
Let us illustrate some variations of a dynamical system using a marble and a pan. We put the marble in the pan. The initial state of the system is the position of the marble, and the dynamical system gives an accurate description of the trajectories of the marble. The marble will obviously move towards the lowest point of the pan. After some oscillation it will finally reach the equilibrium point. In this dynamical system all trajectories converge to the same point. If we perform the same experiment with a marble on a plane surface, the trajectories will not converge to one specific point, but spread out rectilinearly in all directions. A small change in the initial angle will cause an increasing distance between the trajectories, but the growth of the distance will be constant.
The mathematical notion for measuring this sort of dispersion is Lyapunov's exponent. In the plane example Lyapunov's exponent is 0. In the pan, with all trajectories ending in the same point, Lyapunov's exponent is negative. The most interesting case is when Lyapunov's exponent is positive. In this case trajectories may disperse radically, even if their initial states are very close. Lyapunov's exponent gives a quantification of the rate of dispersion. The French mathematician Jacques Hadamard described in 1898 a dynamical system where Lyapunov's exponent is everywhere positive. Thus the dynamical system shows chaotic behaviour everywhere. It is said that Hadamard discovered chaos, at least that he was the first to formally describe a chaotic dynamical system.
The connection between Kolomogorov-Sinai-entropy and Lyapunov's exponent is given in the so-called Pesin's Theorem. A consequence of Pesin's Theorem is that if the entropy is positive, then there exists positive Lyapunov's exponent, and vice versa. The result is by no means obvious. The positive Lyapunov's exponent tells us that trajectories may diverge rapidly, even if their initial states are rather close. Positive Kolomogorov-Sinai-entropy indicates that the system as a whole shows a certain degree of uncertainty. Pesin's theorem says that the two ways of measuring chaotic behaviour of a dynamical system are equivalent.
2. Dynamical billiard.
A dynamical billiard is an idealisation of the game of billiard, but where the table can have shapes other than the rectangular and even be multidimensional. We use only one billiard ball, and the billiard may even have regions where the ball is kept out.
Formally, a dynamical billiard is a dynamical system where a massless and point shaped particle moves inside a bounded region. The particle is reflected by specular reflections at the boundary, without loss of speed. In between two reflections the particle moves rectilinear at constant speed. Remember that a specular reflection is characterised by the law of reflection, the angle of incidence equals the angle of reflection.
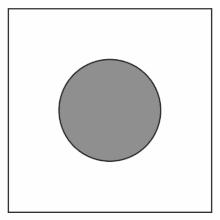
An example of a dynamical billiard is the so-called Sinai's billiard. The table of the Sinai billiard is a square with a disk removed from its centre; the table is flat, having no curvature.
The billiard ball is reflected alternately from the outer and the inner boundary.
Sinai's billiard arises from studying the model of the behaviour of molecules in a so-called ideal gas. In this model we consider the gas as numerous tiny balls (gas molecules) bouncing inside a square, reflecting off the boundaries of the square and off each other. Sinai's billiard provides a simplified, but rather good illustration of this model.
The billiard was introduced by Yakov G Sinai as an example of an interacting Hamiltonian system that displays physical thermo-dynamic properties: all of its possible trajectories are ergodic, and it has positive Lyapunov exponents. Thus the system shows chaotic behaviour. As a model of a classical gas, the Sinai billiard is sometimes called the Lorentz gas. Sinai's great achievement with this model was to show that the behaviour of the gas molecules follows the trajectories of the Hadamard dynamical system, as described by Hadamard in 1898, in the first paper that studied mathematical chaos systematically.
A dynamical billiard doesn't have to be planar. In case of non-zero curvature rectilinear motion is replaced by motion along geodesics, i.e. curves which give the shortest path between points in the billiard. The motion of the ball is geodesic of constant speed, thus the trajectories are completely described by the reflections at the boundary. The system is deterministic, thus if we know the position and the angle of one reflection, the whole trajectory can be determined. The map that takes one state to the next is called the billiard transformation. The billiard transformation determines the dynamical system.
In the ordinary rectangular billiard we observe no chaotic behaviour. A small change in the initial data will induce significant deviation in the long run, but the deviation will be a linear function of time. Chaotic behaviour is characterised by exponential growth in the deviation. For Sinai's billiard chaotic behaviour is observed. For a long time it was assumed that the reason for the exponential deviation of trajectories that are close to each other was the concave shape of the inner boundary. It was also believed that a concave shape was necessary to obtain the chaotic behaviour, just like a concave lens spreads the light.
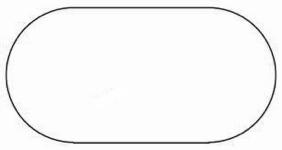
But in 1974 Leonid Bunimovich proved that a billiard table shaped like a stadium, where two opposing sides are replaced by semicircles, produces chaotic behaviour, in spite of the fact that this billiard is completely convex.
3. Entropy of 0, 1-sequences.
We consider a dynamical system where the state space consists of all infinite 0,1-sequences and where the dynamics is given by the shift operator. This dynamical system is named after the great seventeenth century mathematician, Jacob Bernoulli.
Consider the following 0,1-sequence made up of 50 digits:
11010010001010111011011000101010100011100110100011
Do we have any reason to believe that this sequence is randomly generated?
We state some relevant facts about the sequence.
- The sequence contains 25 0's and equally many 1's. This fits with an assumption of randomness.
- In 30 positions the sequence switches from 0 to 1 or vice versa, leaving 19 positions where the next digit is the same as the previous one. In a random sequence these numbers would tend to be the same.
- The sequence contains six subsequences with 3 consecutive digits being equal, but none with 4. In a randomly generated sequence of 50 digits, the probability of finding a subsequence of at least 4 consecutive digits being equal is approximately 98 %. The fact that our sequence has no such subsequence indicates that it is not randomly generated.
The truth is that the sequence is manually generated in an attempt to produce a sequence which looks random. Our mistake, as our small analysis shows, is that we have switched digits too often.
Entropy of Bernoulli schemes
A 0,1-sequence is known as a Bernoulli scheme. In a randomly generated process, we have equal probability for the digits 0 and 1. In our example it seems that the occurrences of 0 and 1 have equal probability, but that the combinations 01 and 10 are more likely, say 60/40 %, than the combinations 00 and 11. This difference in the predictability is quantified in the entropy of the system. The more unpredictable a system is the higher is the entropy. A random 0, 1-sequence has entropy 0.693. Our example has entropy 0.673, which is slightly lower. In general, a Bernoulli scheme of two outcomes of probability and has entropy given by
A Bernoulli scheme may have more than two outcomes. The set of all infinite sequences of letters is a Bernoulli scheme of 26 outcomes. The famous mathematician John von Neumann asked an intriguing question about Bernoulli schemes. He wondered if it is possible that two structurally different Bernoulli schemes can produce the same result. Is it possible to identify the two Bernoulli schemes BS() and BS()? BS stands for Bernoulli scheme and the fractions give the probability for each outcome, thus BS() is the Bernoulli scheme of three outcomes of equal probability.
The solution to the question of von Neumann was finally given by Donald Ornstein in 1970. The answer was no, two essentially different Bernoulli schemes provides different results. The basis for this result was given by Sinai and Kolmogorov in 1959. It turns out that the Kolmogorov-Sinai-entropy is precisely what separates different Bernoulli schemes.
4. The entropy of a dynamical system.
Towards the end of the 1950s, the Russian mathematician Andrey Kolmogorov held a seminar series on dynamical systems at the Moscow University. A question often raised in the seminar concerned the possibility of deciding structural similarity between different dynamical systems. A young seminar participant, Yakov Sinai, presented an affirmative answer, introducing the concept of entropy of a dynamical system.
Let us start by going one decade back in time. In 1948 the American mathematician Claude E Shannon published an article entitled "A Mathematical Theory of Communication". His idea was to use the formalism of mathematics to describe communication as a phenomenon. The purpose of all communication is to convey a message, but how this is done is the messenger's choice. Some will express themselves using numerous words or characters; others prefer to be more brief. The content of the information is the same, but the information density may vary. An example is the so-called SMS language. When sending an SMS message it is common to try to minimise the number of characters. The sentence "I love You" consists of 10 characters, while "IU" consists of only 3, but the content of the two messages is the same.
Shannon introduced the notion of entropy to measure the density of information. To what extent does the next character in the message provide us with more information? High Shannon entropy means that each new character provides new information; low Shannon entropy indicates that the next character just confirms something we already know.
A dynamical system is a description of a physical system and its evolution over time. The system has many states and all states are represented in the state space of the system. A path in the state space describes the dynamics of the dynamical system.
A dynamical system may be deterministic. In a deterministic system no randomness is involved in the development of future states of the system. A swinging pendulum describes a deterministic system. Fixing the position and the speed, the laws of physics will determine the motion of the pendulum. When throwing a dice, we have the other extreme; a stochastic system. The future is completely uncertain; the last toss of the dice has no influence on the next.
In general, we can get a good overview of what happens in a dynamical system in the short term. However, when analysed in the long term, dynamical systems are difficult to understand and predict. The problem of weather forecasting illustrates this phenomenon; the weather condition, described by air pressure, temperature, wind, humidity, etc. is a state of a dynamical system. A weather forecast for the next ten minutes is much more reliable than a weather forecast for the next ten days.
Yakov Sinai was the first to come up with a mathematical foundation for quantifying the complexity of a given dynamical system. Inspired by Shannon's entropy in information theory, and in the framework of Kolmogorov's Moscow seminar, Sinai introduced the concept of entropy for so-called measure-preserving dynamical systems, today known as Kolmogorov-Sinai-entropy. This entropy turned out to be a strong and far-reaching invariant of dynamical systems.
The Kolmogorov-Sinai-entropy provides a rich generalisation of Shannon entropy. In information theory a message is an infinite sequence of symbols, corresponding to a state in the framework of dynamical systems. The shift operator, switching the sequence one step, gives the dynamics of the system. Entropy measures to what extent we are able to predict the next step in the sequence.
Another example concerns a container filled with gas. The state space of this physical system represents states of the gas, i.e. the position and the momentum of every single gas molecule, and the laws of nature determine the dynamics. Again, the degree of complexity and chaotic behaviour of the gas molecules will be the ingredients in the concept of entropy.
Summing up, the Kolmogorov-Sinai-entropy measures unpredictability of a dynamical system. The higher unpredictability, the higher entropy. This fits nicely with Shannon entropy, where unpredictability of the next character is equivalent to new information. It also fits with the concept of entropy in thermodynamics, where disorder increases the entropy, and the fact that disorder and unpredictability are closely related.
Kolmogorov-Sinai-entropy has strongly influenced our understanding of the complexity of dynamical systems. Even though the formal definition is not that complicated, the concept has shown its strength through the highly adequate answers to central problems in the classification of dynamical systems.
Last Updated December 2023