Stirling numbers of the second kind

The Stirling numbers of the second kind

S^{(k)}_n

describe the number of ways a set with n elements can be partitioned into k disjoint, non-empty subsets.

For example, the set {1, 2, 3} can be partitioned into three subsets
in the following way --

{{1}, {2}, {3}},

into two subsets in the following ways --

{{1, 2}, {3}}

{{1, 3}, {2}}

{{1}, {2, 3}},

and into one subset in the following way --

{{1, 2, 3}}.

The numbers can be computed recursively using the formula: $S^{(k)}_n =S^{(k-1)}_n + k S^{(k)}_{n-1}$ .

Here are some diagrams representing the different ways the sets can be
partitioned: a line connects elements in the same subset, and a point represents
a singleton subset.

S2 3

S2 4

S2 5

S2 6

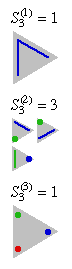
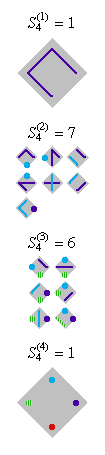
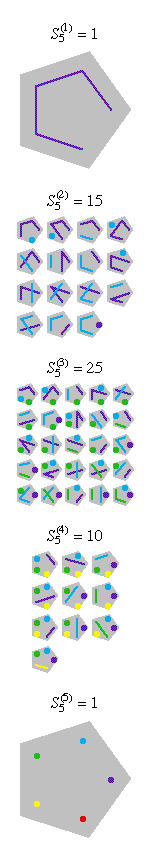
The sums of the Stirling numbers of the second kind: $\sum_{k=0}^n S_n^{(k)}$ are called the Bell numbers.