Michel Talagrand awards
We list below eight awards which have been presented to Michel Talagrand.
We give the extended version of the autobiography he wrote after being awarded the Shaw Prize in 2019 at THIS LINK.
We give the extended version of the autobiography he wrote after being awarded the Abel Prize in 2024 at THIS LINK.
Click on a link below to go to that award
We give the extended version of the autobiography he wrote after being awarded the Shaw Prize in 2019 at THIS LINK.
We give the extended version of the autobiography he wrote after being awarded the Abel Prize in 2024 at THIS LINK.
Click on a link below to go to that award
- Peccot Lectures of the Collège de France (1980)
- Peccot-Vimont Prize of the Collège de France (1980)
- Servant Prize of the Académie des sciences (1985)
- Line and Michel Loève Prize in Probability (1995)
- Fermat Prize for mathematical research (1997)
- Shaw Prize in mathematics (2019)
- Stefan Banach Medal of the Polish Academy of Sciences (2022)
- The Abel Prize (2024)
1. Peccot Lectures of the Collège de France (1980).
1.1. The Peccot Lectures.
Since 1885, thanks to an endowment from the family of the mathematician Claude-Antoine Peccot, the Collège de France has rewarded each year young mathematicians under 30 years of age who have distinguished themselves in the field of theoretical or applied mathematics.
The Peccot course is a one-semester mathematics course at the Collège de France. Each course is given by a mathematician under the age of thirty who has distinguished themselves by their promising first work. The course consists of a series of lectures which allow the winner to present their recent research. Being a lecturer on a Peccot course is a distinction that often foreshadows an exceptional scientific career; among them are future holders of the Fields medal, the Abel prize, academicians and professors at the Collège de France. The first to deliver the Cours Peccot were Émile Borel (1899-1902), Henri Lebesgue (1902-03) and René Baire (1903-04).
1.2. Michel Talagrand's Peccot Lectures.
Michel Talagrand delivered the Peccot lectures on Compacts de fonctions mesurables et applications in 1980.
2. Peccot-Vimont Prize of the Collège de France (1980).
Since 1885, thanks to an endowment from the family of the mathematician Claude-Antoine Peccot, the Collège de France has rewarded each year young mathematicians under 30 years of age who have distinguished themselves in the field of theoretical or applied mathematics.
The Peccot course is a one-semester mathematics course at the Collège de France. Each course is given by a mathematician under the age of thirty who has distinguished themselves by their promising first work. The course consists of a series of lectures which allow the winner to present their recent research. Being a lecturer on a Peccot course is a distinction that often foreshadows an exceptional scientific career; among them are future holders of the Fields medal, the Abel prize, academicians and professors at the Collège de France. The first to deliver the Cours Peccot were Émile Borel (1899-1902), Henri Lebesgue (1902-03) and René Baire (1903-04).
1.2. Michel Talagrand's Peccot Lectures.
Michel Talagrand delivered the Peccot lectures on Compacts de fonctions mesurables et applications in 1980.
2.1. The Peccot-Vimont Prize.
Some Peccot lecturers may, exceptionally, also be awarded the separate Peccot-Vimont Prize. The Peccot course is part of a series of events at the Collège de France, financed and managed by legacies from the family of Claude-Antoine Peccot gathered in the Claude-Antoine Peccot Foundation created by his family in tribute to Claude-Antoine Peccot, a young mathematician who died at the age of 20. This foundation first made it possible to create an annual scholarship, transformed into a lectureship from 1900. Several successive donations (in 1886, in 1894, in 1897, gathered in 1902) by Julie Anne Antoinette Peccot and Claudine Henriette Marguerite Lafond, widow of André Eugène Vimont, respectively the mother and godmother of Claude-Antoine Peccot made it possible to create scholarships, later transformed into prizes.
2.2. Michel Talagrand's Peccot-Vimont Prize.
Michel Talagrand was awarded the Peccot-Vimont Prize by the Collège de France in 1980.
3. Servant Prize of the Académie des sciences (1985).
Some Peccot lecturers may, exceptionally, also be awarded the separate Peccot-Vimont Prize. The Peccot course is part of a series of events at the Collège de France, financed and managed by legacies from the family of Claude-Antoine Peccot gathered in the Claude-Antoine Peccot Foundation created by his family in tribute to Claude-Antoine Peccot, a young mathematician who died at the age of 20. This foundation first made it possible to create an annual scholarship, transformed into a lectureship from 1900. Several successive donations (in 1886, in 1894, in 1897, gathered in 1902) by Julie Anne Antoinette Peccot and Claudine Henriette Marguerite Lafond, widow of André Eugène Vimont, respectively the mother and godmother of Claude-Antoine Peccot made it possible to create scholarships, later transformed into prizes.
2.2. Michel Talagrand's Peccot-Vimont Prize.
Michel Talagrand was awarded the Peccot-Vimont Prize by the Collège de France in 1980.
3.1. The Servant Prize.
The Servant Prize, created in 1952, is a prize awarded every two years by the French Academy of Sciences, alternately in the fields of mathematical sciences and physical sciences. The Servant Prize is named for French mathematician Maurice Servant (1877-1952) who was awarded the Bordin Prize in 1904.
3.2. Michel Talagrand's Servant Prize.
Michel Talagrand was awarded the Servant Prize by the Académie des sciences in 1985.
4. Line and Michel Loève Prize in Probability (1995).
The Servant Prize, created in 1952, is a prize awarded every two years by the French Academy of Sciences, alternately in the fields of mathematical sciences and physical sciences. The Servant Prize is named for French mathematician Maurice Servant (1877-1952) who was awarded the Bordin Prize in 1904.
3.2. Michel Talagrand's Servant Prize.
Michel Talagrand was awarded the Servant Prize by the Académie des sciences in 1985.
4.1. The Loève Prize.
Michel Loève was Professor at the University of California, Berkeley, from 1948 until his untimely death in 1979. His widow, Line Loève, shortly before her own death in 1992 gave a very generous bequest to the University of California, Berkeley in two parts. One part established the Loève Fellowships to support graduate students in probability. The other part established the Loève Prize, formally The Line and Michel Loève International Prize in Probability. The prize, awarded every two years, is intended to recognise outstanding contributions by researchers in probability who are under 45 years old. As specified in the bequest, the recipient is chosen by a selection committee of about 25 distinguished probabilists.
4.2. Michel Talagrand's Loève Prize.
Michel Talagrand was awarded the Loève Prize by the University of California, Berkeley in 1995. He was the second laureate, the first in 1993 being the British probabilist David John Aldous. The third laureate was Jean-François Le Gall.
5. Fermat Prize for mathematical research (1997).
Michel Loève was Professor at the University of California, Berkeley, from 1948 until his untimely death in 1979. His widow, Line Loève, shortly before her own death in 1992 gave a very generous bequest to the University of California, Berkeley in two parts. One part established the Loève Fellowships to support graduate students in probability. The other part established the Loève Prize, formally The Line and Michel Loève International Prize in Probability. The prize, awarded every two years, is intended to recognise outstanding contributions by researchers in probability who are under 45 years old. As specified in the bequest, the recipient is chosen by a selection committee of about 25 distinguished probabilists.
4.2. Michel Talagrand's Loève Prize.
Michel Talagrand was awarded the Loève Prize by the University of California, Berkeley in 1995. He was the second laureate, the first in 1993 being the British probabilist David John Aldous. The third laureate was Jean-François Le Gall.
5.1. The Fermat Prize.
The Fermat Prize for research in mathematics rewards the research work of mathematicians in fields where Pierre de Fermat's contributions were decisive: (i) statements of variational principles; (ii) foundations of the calculus of probabilities and of analytic geometry; and (iii) number theory. Within these fields, the spirit of the prize is to reward results which are accessible to the greatest number of professional mathematicians. The jury will consider young mathematicians only (no older than 45 at the time of the submission of their application) and will prefer recent research results (obtained during the last five years). Since 1989, The Fermat Prize is awarded every two years by the Institute of Mathematics of Toulouse, under the aegis of Université Paul Sabatier. The prize ceremony includes:
- a lecture delivered by the winner at the Toulouse Institute of Mathematics;
- a prize-awarding ceremony at the Paul Sabatier University.
The recipient will publish a survey article about the award-winning research work in the journal Annales de la Faculté des Sciences de Toulouse; this paper should be accessible to professional mathematicians who are not experts on the subject and will explain the significance of the award-winning results.
5.2. Michel Talagrand's Fermat Prize.
Michel Talagrand was awarded the Fermat Prize by the Institute of Mathematics of Toulouse, under the aegis of Université Paul Sabatier in 1997:-
In 1998 Michel Talagrand published Rigorous results for the Hopfield model with many patterns. A review by Anton Bovier begins by describing the areas of Talagrand's work:-
6. Shaw Prize in mathematics (2019).
The Fermat Prize for research in mathematics rewards the research work of mathematicians in fields where Pierre de Fermat's contributions were decisive: (i) statements of variational principles; (ii) foundations of the calculus of probabilities and of analytic geometry; and (iii) number theory. Within these fields, the spirit of the prize is to reward results which are accessible to the greatest number of professional mathematicians. The jury will consider young mathematicians only (no older than 45 at the time of the submission of their application) and will prefer recent research results (obtained during the last five years). Since 1989, The Fermat Prize is awarded every two years by the Institute of Mathematics of Toulouse, under the aegis of Université Paul Sabatier. The prize ceremony includes:
- a lecture delivered by the winner at the Toulouse Institute of Mathematics;
- a prize-awarding ceremony at the Paul Sabatier University.
The recipient will publish a survey article about the award-winning research work in the journal Annales de la Faculté des Sciences de Toulouse; this paper should be accessible to professional mathematicians who are not experts on the subject and will explain the significance of the award-winning results.
5.2. Michel Talagrand's Fermat Prize.
Michel Talagrand was awarded the Fermat Prize by the Institute of Mathematics of Toulouse, under the aegis of Université Paul Sabatier in 1997:-
... for his fundamental contributions in various domains of Probability.5.3. Michel Talagrand's work leading to the Prize.
In 1998 Michel Talagrand published Rigorous results for the Hopfield model with many patterns. A review by Anton Bovier begins by describing the areas of Talagrand's work:-
Two models of disordered systems have been the focus of attention for theoretical and mathematical physics over the last two decades: the Sherrington-Kirkpatrick model and the Hopfield model. They were proposed in the 1970s as the simplest "solvable" mean field models for spin glasses (the Hopfield model having attracted much attention in the field of neural networks as the simplest model of an associative memory). Both models have been solved on the level of heuristic theoretical physics by use of the "replica trick" and the intricate "replica symmetry breaking" scheme devised by Parisi and coworkers. These solutions reveal a richness of structure that would be hard to suspect a priori in such simple models, and this has not failed to attract attempts to obtain a mathematically rigorous understanding of these models. In the Hopfield model in particular, in various regimes of the parameters of the model, simplifications occur that have allowed progress in the rigorous understanding of this system.
6.1. The Shaw Prize.
The Shaw Prize was established under the vision and generosity of the late Mr Run Run Shaw in 2002. It is an international award to honour individuals who are currently active in their respective fields and who have recently achieved distinguished and significant advances, who have made outstanding contributions in academic and scientific research or applications, or who in other domains have achieved excellence. The award is dedicated to furthering societal progress, enhancing quality of life, and enriching humanity's spiritual civilisation.
The Shaw Prize consists of three disciplines, namely, Astronomy, Life Science and Medicine, and Mathematical Sciences and is presented annually by the Shaw Prize Foundation since 2004. Mathematical Sciences are one of the three disciplines for the following reason:
The Shaw Prize in Mathematical Sciences 2019 was awarded to Michel Talagrand:-
Michel Talagrand has made profound contributions to probability and high-dimensional geometry, at least three of which could be described as revolutionary.
A first major theme of Talagrand's research is the study of suprema of stochastic processes. A stochastic process is a collection of interacting random variables. When one is given a large such collection, it is often of crucial importance to obtain information about how its maximum value is distributed. Starting with the case of Gaussian processes (here the random variables each have a Gaussian distribution, given by the famous "bell curve", and can be correlated in a certain way) and then for more general cases, Talagrand has developed tools, such as majorizing measures or generic chaining, that provide powerful and very useful bounds for how these maximum values behave.
The second group of contributions concerns a phenomenon known as concentration of measure. Broadly speaking, this says that many functions that depend on a large number of reasonably independent random variables are extremely likely to take values close to their average. For example, if one tosses a coin a thousand times, then the probability that the number of heads will be between 450 and 550 is roughly 99.7 percent, and the probability that it will be more than 600 is approximately two millionths of one percent. In such a situation, we say that the number of heads is concentrated. This phenomenon, often associated with the name of the mathematician Vitali Milman, is remarkably general and has a multitude of applications in areas as diverse as the geometry of convex bodies, graph theory, and theoretical computer science. One of Talagrand's great achievements has been to examine this phenomenon in detail and hugely improve our understanding of it. In particular, he proved famous inequalities, using completely new techniques, that give new concentration results that are widely used in many different important settings.
A third family of results for which he is famous concern objects known as spin glasses, which provide a mathematical model of a physical phenomenon involving very disordered systems. Unlike many models from statistical physics, spin glasses have a double layer of randomness. First, the way in which different random variables (the spins in the spin glass language) will interact is chosen at random, which creates a very complex energy landscape, and then the random variables themselves are sampled randomly. One would then like to understand this large family of randomly interacting random variables and describe its typical features. Spin glasses have a short and simple definition, but they are notoriously hard to analyse. A significant advance was made by the theoretical physicist, Giorgio Parisi, who proposed a formula for the free energy of a spin glass, which is an important quantity that encapsulates information about this random energy landscape. However, turning predictions of statistical physicists into mathematically rigorous arguments is often extremely hard, and a rich source of fascinating mathematical problems. Finding a complete rigorous proof in this case seemed to be way beyond what was it was realistic to hope for, despite remarkable insights and progress by Francesco Guerra, but Talagrand managed to do it, thereby providing for the first time a complete mathematical underpinning for this extremely important physical theory.
One notable feature of Talagrand's career that marks him out from many other mathematicians is that when he solves a problem, he does not just leave it and move on. Rather, he continues to work on it, improving his understanding and reworking his arguments until he has a well-developed theory that can be more easily used by other mathematicians. He has written monumental and highly influential textbooks on all the three topics just mentioned, and these have played a very significant part in the spread of his ideas, which are now central to the work of large numbers of other mathematicians. Talagrand is a true one-off, nearly always working on his own, and obtaining extraordinary and highly unexpected results that have changed the mathematical landscape.
6.4. Talagrand's acceptance speech.
Honourable Chief Executive,
Members of the Shaw Prize Council and Selection Committees
Ladies and Gentlemen
It is an immense and unexpected honour for me to receive the Shaw Prize today.
In the long chain of extremely unlikely events which brought me here, Hong-Kong played a small but crucial part.
The luckiest event of my life is to have met in Kent, Ohio, a stupendous PhD student who instantly captured my heart to this day. I proposed to her after three days. You are crazy, she said. I followed her to Korea.
She sent me back to France with a broken heart. On the way home, I stopped over in Hong-Kong. I had the address of a fantastic wholesaler, where I bought her as a parting gift the best pearl necklace I could afford. This unselfish deed moved her, and the story continued.
Her father was a well-known scholar in Korea, and had raised his children in the belief that scholarly achievement is the supreme value in life. I have often wondered if this belief had more to do in her decision to share my life than my good looks. Despite having a full professional life, she has been extraordinarily supportive. I never heard the words I dreaded the most: Now is not the time to work. This does not mean that I did not see my family. The secret of success in mathematic is to work every day until exhaustion, but not more. Do not believe her when she says I devoted 99% of my life to mathematics and 1% to her. She got at least 2%.
Having the perfect spouse, all the rest was easy. I wish I could say that I had a grand vision of mathematics but the reality is very different. I know little mathematics. I simply tried solving problems which came my way, always attempting to go to the bottom of things. I did not work on fashionable areas, but I focused on simple universal structures because there lay important questions. I owe a great debt to Gilles Pisier, Vitali Milman, and others, who introduced me to the areas where I became the most successful. Modern science is like a magnificent temple in perpetual construction. I am proud I could contribute one small brick to its foundations.
6.5. The Shaw Prize Lecture 2019.
Michel Talagrand delivered the 2019 Shaw Prize Lecture "Mysteries in High Dimensions".
6.6. Michel Talagrand's biography.
Michel Talagrand was born in 1952 in France. He obtained his PhD in Mathematical Sciences in 1977 from the University of Paris VI, France. From 1974 until his retirement in 2017, he was part of the Functional Analysis Team of the Institute of Mathematics of the University Paris IV. He was successively Research Trainee, Research Associate, Researcher and Senior Researcher for the French National Centre for Scientific Research (CNRS). He is a member of the French Academy of Sciences. Talagrand has been the recipient of the Peccot-Vimont Prize of the French Collège de France (1980), the Servant Prize of the French Académie des Sciences (1985), the Loève Prize (1995), and the Fermat Prize (1997). He was an invited speaker at the International Congress of Mathematicians (ICM) in 1990 and an ICM plenary speaker in 1998.
6.7. Michel Talagrand's autobiography.
My four grandparents were born very poor into large peasant families. Against all odds they managed to give my parents access to higher education. My father became a mathematics professor and it was he who sparked my interest in science.
I was born with congenital defective retinas and lost one eye at age five. When I was fifteen, I suffered from several consecutive retinal detachments in the remaining eye, causing me to miss school for half a year. Fearing that I would shortly become blind, I focused my energy on studying. I learned that this focus and hard work could make me competent in mathematics and physics. I did not attend an elite university, but the local university in Lyon close to where my parents lived. My university years were very happy and I built a solid foundation in mathematics.
My great luck is that the National Centre of Scientific Research offered me, in 1974, a research position, even though I had not yet done any research. This was uncommon, and the last year that such positions were offered. I have treasured this position all my life as it allowed me to work without any constraint on the topics of my liking.
I started doing research in the Functional Analysis group of Professor Choquet in Paris, where I completed my PhD. Professor Choquet's mathematics were supremely elegant and seemed effortless. Unfortunately, this is not the style I was born for, but several of my later contributions would not have been possible if I had not been inspired by his vision of mathematics. My interests shifted over the years but I belonged to this group for my entire career. Paris is a fantastic place to be a mathematician. Many mathematical stars work there and there are so many prominent visitors. I benefitted immensely from interaction with these visitors, and with my colleagues, at the numerous conferences I attended, but overall, I had few collaborators.
Thanks to mathematics, I met a wonderful woman who highly valued academic achievement. She has supported my work in every conceivable way, as well as bringing me so much personal happiness.
I developed an early interest in measure theory. While in the seventies this theory was well past its prime, it helped me learn to look at things in an abstract way, which served me well later in my career. It also triggered my interest in Banach Spaces, although it was clear that I could not have the same impact as the leaders in the field. The arrival of Gilles Pisier in our group, in 1983, was a turning point for me. Gilles shared his private notes on Probability in Banach Spaces, an area that I could then learn and where I eventually became successful. He also directed me to the problem of characterising the continuity of Gaussian processes, on which X Fernique had made determining advances, and which I was able to solve in 1985. This started my work on upper and lower bounds of stochastic processes. Pisier's influence changed the very nature of my work, which became far more quantitative.
I was also greatly influenced by Vitali Milman, who was most energetically expounding the concept of concentration of measure. I did not understand the depth of this concept at first, but it directed me to the discovery of several "concentration inequalities" that have since proved useful. The most important of these required taking a convex hull, and certainly this was easier to discover having been a student of Gustave Choquet.
I started mathematics with the modest goal of making a living out of it and began by working on small problems in somewhat exotic areas. My interests later shifted towards more central areas of mathematics, but I always worked on the problems I enjoyed the most, following my own preference. The path of discovery in mathematics can be very tortuous. The discovery of new classes of concentration inequalities stemmed from considering a problem of seemingly secondary interest. Many times, what I had learned by writing a paper of trifling importance proved a key step in a far more substantial theorem.
Rather late in life, I attacked a well-established problem in theoretical physics. The physicists were studying purely mathematical objects (called spin glasses) using methods which do not belong to mathematics. It was an all-consuming eight-year effort to prove that mathematics could bring a far more solid solution to this problem.
In later years, I have tried to write textbooks to communicate the experience of a lifetime in probability theory and have not shied away from reworking them over and over.
The Shaw Foundation recognition is an honour I could never have dreamed of. It will allow me to set up a far more modest mathematical prize recognizing the achievements of young researchers in the areas to which I have devoted my life.
7. Stefan Banach Medal of the Polish Academy of Sciences (2022).
The Shaw Prize was established under the vision and generosity of the late Mr Run Run Shaw in 2002. It is an international award to honour individuals who are currently active in their respective fields and who have recently achieved distinguished and significant advances, who have made outstanding contributions in academic and scientific research or applications, or who in other domains have achieved excellence. The award is dedicated to furthering societal progress, enhancing quality of life, and enriching humanity's spiritual civilisation.
The Shaw Prize consists of three disciplines, namely, Astronomy, Life Science and Medicine, and Mathematical Sciences and is presented annually by the Shaw Prize Foundation since 2004. Mathematical Sciences are one of the three disciplines for the following reason:
Mathematics is the basic language of all natural sciences and all modern technology. In the twentieth century mathematics made tremendous strides both in opening new frontiers and in solving important and difficult old problems. Its influence permeates every creative scientific and technological discipline, and extends into the social science. With the developments in computer science, information technology, and statistics in the twentieth century, the importance of mathematics to mankind will be further enhanced in the twenty-first century.6.2. Michel Talagrand's Shaw Prize.
The Shaw Prize in Mathematical Sciences 2019 was awarded to Michel Talagrand:-
... for his work on concentration inequalities, on suprema of stochastic processes and on rigorous results for spin glasses.6.3. The Contribution of Michel Talagrand.
Michel Talagrand has made profound contributions to probability and high-dimensional geometry, at least three of which could be described as revolutionary.
A first major theme of Talagrand's research is the study of suprema of stochastic processes. A stochastic process is a collection of interacting random variables. When one is given a large such collection, it is often of crucial importance to obtain information about how its maximum value is distributed. Starting with the case of Gaussian processes (here the random variables each have a Gaussian distribution, given by the famous "bell curve", and can be correlated in a certain way) and then for more general cases, Talagrand has developed tools, such as majorizing measures or generic chaining, that provide powerful and very useful bounds for how these maximum values behave.
The second group of contributions concerns a phenomenon known as concentration of measure. Broadly speaking, this says that many functions that depend on a large number of reasonably independent random variables are extremely likely to take values close to their average. For example, if one tosses a coin a thousand times, then the probability that the number of heads will be between 450 and 550 is roughly 99.7 percent, and the probability that it will be more than 600 is approximately two millionths of one percent. In such a situation, we say that the number of heads is concentrated. This phenomenon, often associated with the name of the mathematician Vitali Milman, is remarkably general and has a multitude of applications in areas as diverse as the geometry of convex bodies, graph theory, and theoretical computer science. One of Talagrand's great achievements has been to examine this phenomenon in detail and hugely improve our understanding of it. In particular, he proved famous inequalities, using completely new techniques, that give new concentration results that are widely used in many different important settings.
A third family of results for which he is famous concern objects known as spin glasses, which provide a mathematical model of a physical phenomenon involving very disordered systems. Unlike many models from statistical physics, spin glasses have a double layer of randomness. First, the way in which different random variables (the spins in the spin glass language) will interact is chosen at random, which creates a very complex energy landscape, and then the random variables themselves are sampled randomly. One would then like to understand this large family of randomly interacting random variables and describe its typical features. Spin glasses have a short and simple definition, but they are notoriously hard to analyse. A significant advance was made by the theoretical physicist, Giorgio Parisi, who proposed a formula for the free energy of a spin glass, which is an important quantity that encapsulates information about this random energy landscape. However, turning predictions of statistical physicists into mathematically rigorous arguments is often extremely hard, and a rich source of fascinating mathematical problems. Finding a complete rigorous proof in this case seemed to be way beyond what was it was realistic to hope for, despite remarkable insights and progress by Francesco Guerra, but Talagrand managed to do it, thereby providing for the first time a complete mathematical underpinning for this extremely important physical theory.
One notable feature of Talagrand's career that marks him out from many other mathematicians is that when he solves a problem, he does not just leave it and move on. Rather, he continues to work on it, improving his understanding and reworking his arguments until he has a well-developed theory that can be more easily used by other mathematicians. He has written monumental and highly influential textbooks on all the three topics just mentioned, and these have played a very significant part in the spread of his ideas, which are now central to the work of large numbers of other mathematicians. Talagrand is a true one-off, nearly always working on his own, and obtaining extraordinary and highly unexpected results that have changed the mathematical landscape.
6.4. Talagrand's acceptance speech.
Honourable Chief Executive,
Members of the Shaw Prize Council and Selection Committees
Ladies and Gentlemen
It is an immense and unexpected honour for me to receive the Shaw Prize today.
In the long chain of extremely unlikely events which brought me here, Hong-Kong played a small but crucial part.
The luckiest event of my life is to have met in Kent, Ohio, a stupendous PhD student who instantly captured my heart to this day. I proposed to her after three days. You are crazy, she said. I followed her to Korea.
She sent me back to France with a broken heart. On the way home, I stopped over in Hong-Kong. I had the address of a fantastic wholesaler, where I bought her as a parting gift the best pearl necklace I could afford. This unselfish deed moved her, and the story continued.
Her father was a well-known scholar in Korea, and had raised his children in the belief that scholarly achievement is the supreme value in life. I have often wondered if this belief had more to do in her decision to share my life than my good looks. Despite having a full professional life, she has been extraordinarily supportive. I never heard the words I dreaded the most: Now is not the time to work. This does not mean that I did not see my family. The secret of success in mathematic is to work every day until exhaustion, but not more. Do not believe her when she says I devoted 99% of my life to mathematics and 1% to her. She got at least 2%.
Having the perfect spouse, all the rest was easy. I wish I could say that I had a grand vision of mathematics but the reality is very different. I know little mathematics. I simply tried solving problems which came my way, always attempting to go to the bottom of things. I did not work on fashionable areas, but I focused on simple universal structures because there lay important questions. I owe a great debt to Gilles Pisier, Vitali Milman, and others, who introduced me to the areas where I became the most successful. Modern science is like a magnificent temple in perpetual construction. I am proud I could contribute one small brick to its foundations.
6.5. The Shaw Prize Lecture 2019.
Michel Talagrand delivered the 2019 Shaw Prize Lecture "Mysteries in High Dimensions".
6.6. Michel Talagrand's biography.
Michel Talagrand was born in 1952 in France. He obtained his PhD in Mathematical Sciences in 1977 from the University of Paris VI, France. From 1974 until his retirement in 2017, he was part of the Functional Analysis Team of the Institute of Mathematics of the University Paris IV. He was successively Research Trainee, Research Associate, Researcher and Senior Researcher for the French National Centre for Scientific Research (CNRS). He is a member of the French Academy of Sciences. Talagrand has been the recipient of the Peccot-Vimont Prize of the French Collège de France (1980), the Servant Prize of the French Académie des Sciences (1985), the Loève Prize (1995), and the Fermat Prize (1997). He was an invited speaker at the International Congress of Mathematicians (ICM) in 1990 and an ICM plenary speaker in 1998.
6.7. Michel Talagrand's autobiography.
My four grandparents were born very poor into large peasant families. Against all odds they managed to give my parents access to higher education. My father became a mathematics professor and it was he who sparked my interest in science.
I was born with congenital defective retinas and lost one eye at age five. When I was fifteen, I suffered from several consecutive retinal detachments in the remaining eye, causing me to miss school for half a year. Fearing that I would shortly become blind, I focused my energy on studying. I learned that this focus and hard work could make me competent in mathematics and physics. I did not attend an elite university, but the local university in Lyon close to where my parents lived. My university years were very happy and I built a solid foundation in mathematics.
My great luck is that the National Centre of Scientific Research offered me, in 1974, a research position, even though I had not yet done any research. This was uncommon, and the last year that such positions were offered. I have treasured this position all my life as it allowed me to work without any constraint on the topics of my liking.
I started doing research in the Functional Analysis group of Professor Choquet in Paris, where I completed my PhD. Professor Choquet's mathematics were supremely elegant and seemed effortless. Unfortunately, this is not the style I was born for, but several of my later contributions would not have been possible if I had not been inspired by his vision of mathematics. My interests shifted over the years but I belonged to this group for my entire career. Paris is a fantastic place to be a mathematician. Many mathematical stars work there and there are so many prominent visitors. I benefitted immensely from interaction with these visitors, and with my colleagues, at the numerous conferences I attended, but overall, I had few collaborators.
Thanks to mathematics, I met a wonderful woman who highly valued academic achievement. She has supported my work in every conceivable way, as well as bringing me so much personal happiness.
I developed an early interest in measure theory. While in the seventies this theory was well past its prime, it helped me learn to look at things in an abstract way, which served me well later in my career. It also triggered my interest in Banach Spaces, although it was clear that I could not have the same impact as the leaders in the field. The arrival of Gilles Pisier in our group, in 1983, was a turning point for me. Gilles shared his private notes on Probability in Banach Spaces, an area that I could then learn and where I eventually became successful. He also directed me to the problem of characterising the continuity of Gaussian processes, on which X Fernique had made determining advances, and which I was able to solve in 1985. This started my work on upper and lower bounds of stochastic processes. Pisier's influence changed the very nature of my work, which became far more quantitative.
I was also greatly influenced by Vitali Milman, who was most energetically expounding the concept of concentration of measure. I did not understand the depth of this concept at first, but it directed me to the discovery of several "concentration inequalities" that have since proved useful. The most important of these required taking a convex hull, and certainly this was easier to discover having been a student of Gustave Choquet.
I started mathematics with the modest goal of making a living out of it and began by working on small problems in somewhat exotic areas. My interests later shifted towards more central areas of mathematics, but I always worked on the problems I enjoyed the most, following my own preference. The path of discovery in mathematics can be very tortuous. The discovery of new classes of concentration inequalities stemmed from considering a problem of seemingly secondary interest. Many times, what I had learned by writing a paper of trifling importance proved a key step in a far more substantial theorem.
Rather late in life, I attacked a well-established problem in theoretical physics. The physicists were studying purely mathematical objects (called spin glasses) using methods which do not belong to mathematics. It was an all-consuming eight-year effort to prove that mathematics could bring a far more solid solution to this problem.
In later years, I have tried to write textbooks to communicate the experience of a lifetime in probability theory and have not shied away from reworking them over and over.
The Shaw Foundation recognition is an honour I could never have dreamed of. It will allow me to set up a far more modest mathematical prize recognizing the achievements of young researchers in the areas to which I have devoted my life.
7.1. The Stefan Banach Medal.
The Stefan Banach Medal is awarded to individuals by the Presidium of the Polish Academy of Sciences (PAN) in recognition of outstanding contributions to the development of mathematical sciences. The Stefan Banach Medal was established in 1992, marking the centenary of Stefan Banach's birth.
7.2. Banach Medal to Professor Michel Talagrand.
The Stefan Banach Medal 2022 was awarded to Michel Talagrand on 8 September 2022. The ceremony of awarding the Stefan Banach Medal to Professor Michel Talagrand, was held at the Institute of Mathematics of the Polish Academy of Sciences on 8 September 2022 at 2 pm in room 321 (3rd floor) at Sniadeckich 8 in Warsaw.
Schedule of the award ceremony:
2 pm - award ceremony in room 321,
2:30 pm - refreshments in room 409,
3 pm - laureate's lecture in room 321.
The chairman of the jury which selected Michel Talagrand for the 2022 Stefan Banach Medal was Feliks Przycki. He delivered the following laudation of Professor Michel Talagrand on the occasion of being awarded the Banach Medal by the Polish Academy of Sciences:
Professor Michel Talagrand was awarded in 2022 the Stefan Banach Medal by the Polish Academy of Sciences:
Michel Talagrand is a full member of the French Academy of Sciences and a recipient of prestigious international awards: the Loeve prize in 1995, the Fermat prize in 1997 and the Shaw prize in 2019. He was a plenary speaker at the ICM in Berlin in 1998.
Some of his pivotal results are:
- concentration of measure and isoperimetric inequalities for product measures, having many applications and generalisations,
- characterisation of Gaussian processes with continuous trajectories, related to almost sure convergence of random series in Banach spaces,
- estimates of suprema of stochastic processes, chaining methods.
- proof of the Parisi formula computing "free energy" in any temperature (Annals of Mathematics 2006). F Germinate in his review in Math. Rev. wrote "it was the most celebrated longstanding open problem in the area of spin glasses".
He is the author of several fundamental books. One should mention:
- "What is Quantum Field Theory" Cambridge 2022;
- "Upper and Lower Bounds for Stochastic Processes, Modern methods and classical problems", Springer-Verlag 2014, where results of Witold Bednorz and Rafał Latała from the University of Warsaw and Adam Paszkiewicz from the University of Łódz are discussed;
- "The generic chaining. Upper and lower bounds of stochastic processes", Springer-Verlag 2005.
- "Probability in Banach spaces. Isoperimetry and processes" joint with Michel Ledoux, Springer-Verlag 1991, cited 1138 times according to MathSciNet;
- "Spin glasses: a challenge for mathematicians. Cavity and mean field models", Springer-Verlag 2003.
The mathematicians who nominated Michel Talagrand for the Banach Medal wrote: "Astonishing is the richness and value of his achieved results. None of them is "easy". They demand a lot of perseverance and extraordinary deep insight. Many of them are solutions of famous old problems."
7.3. Michel Talagrand's lecture.
The Stefan Banach Medal lecture Michel Talagrand delivered was Chaining: a long story. He discussed his generic chaining method, which is widely used in machine learning, data mining, finance and economics, as well as in genomics and drug discovery. He began the lecture as follows:-
- Chaining was invented by A Kolmogorov to control the supremum of a stochastic process.
- Following 40 years of work we now know that for many natural classes of processes, it is optimal.
- The proof of optimality is still very difficult. Probably far too difficult. Probably some key ideas are still missing.
8. The Abel Prize (2024).
The Stefan Banach Medal is awarded to individuals by the Presidium of the Polish Academy of Sciences (PAN) in recognition of outstanding contributions to the development of mathematical sciences. The Stefan Banach Medal was established in 1992, marking the centenary of Stefan Banach's birth.
7.2. Banach Medal to Professor Michel Talagrand.
The Stefan Banach Medal 2022 was awarded to Michel Talagrand on 8 September 2022. The ceremony of awarding the Stefan Banach Medal to Professor Michel Talagrand, was held at the Institute of Mathematics of the Polish Academy of Sciences on 8 September 2022 at 2 pm in room 321 (3rd floor) at Sniadeckich 8 in Warsaw.
Schedule of the award ceremony:
2 pm - award ceremony in room 321,
2:30 pm - refreshments in room 409,
3 pm - laureate's lecture in room 321.
The chairman of the jury which selected Michel Talagrand for the 2022 Stefan Banach Medal was Feliks Przycki. He delivered the following laudation of Professor Michel Talagrand on the occasion of being awarded the Banach Medal by the Polish Academy of Sciences:
Professor Michel Talagrand was awarded in 2022 the Stefan Banach Medal by the Polish Academy of Sciences:
... for groundbreaking results in functional analysis, the theory of Banach spaces, probability theory and in statistical mechanics: the theory of "spin glasses".His results inspired the research of outstanding Polish mathematicians.
Michel Talagrand is a full member of the French Academy of Sciences and a recipient of prestigious international awards: the Loeve prize in 1995, the Fermat prize in 1997 and the Shaw prize in 2019. He was a plenary speaker at the ICM in Berlin in 1998.
Some of his pivotal results are:
- concentration of measure and isoperimetric inequalities for product measures, having many applications and generalisations,
- characterisation of Gaussian processes with continuous trajectories, related to almost sure convergence of random series in Banach spaces,
- estimates of suprema of stochastic processes, chaining methods.
- proof of the Parisi formula computing "free energy" in any temperature (Annals of Mathematics 2006). F Germinate in his review in Math. Rev. wrote "it was the most celebrated longstanding open problem in the area of spin glasses".
He is the author of several fundamental books. One should mention:
- "What is Quantum Field Theory" Cambridge 2022;
- "Upper and Lower Bounds for Stochastic Processes, Modern methods and classical problems", Springer-Verlag 2014, where results of Witold Bednorz and Rafał Latała from the University of Warsaw and Adam Paszkiewicz from the University of Łódz are discussed;
- "The generic chaining. Upper and lower bounds of stochastic processes", Springer-Verlag 2005.
- "Probability in Banach spaces. Isoperimetry and processes" joint with Michel Ledoux, Springer-Verlag 1991, cited 1138 times according to MathSciNet;
- "Spin glasses: a challenge for mathematicians. Cavity and mean field models", Springer-Verlag 2003.
The mathematicians who nominated Michel Talagrand for the Banach Medal wrote: "Astonishing is the richness and value of his achieved results. None of them is "easy". They demand a lot of perseverance and extraordinary deep insight. Many of them are solutions of famous old problems."
7.3. Michel Talagrand's lecture.
The Stefan Banach Medal lecture Michel Talagrand delivered was Chaining: a long story. He discussed his generic chaining method, which is widely used in machine learning, data mining, finance and economics, as well as in genomics and drug discovery. He began the lecture as follows:-
- Chaining was invented by A Kolmogorov to control the supremum of a stochastic process.
- Following 40 years of work we now know that for many natural classes of processes, it is optimal.
- The proof of optimality is still very difficult. Probably far too difficult. Probably some key ideas are still missing.
8.1. History of the Abel Prize.
The Abel Prize was awarded for the first time in 2003 but it was first suggested over 100 years earlier. Sophus Lie, when he saw that Nobel's plans for annual prizes did not include one for mathematics, proposed the setting up of an Abel Prize which would be awarded every five years for outstanding work in pure mathematics. Lie's effort was, by all accounts, inspired by the ongoing collection for the Nansen Fund and he contacted mathematicians world-wide and gathered wide support. However he had not set up any machinery to carry the idea forward and when he died soon after this, in 1899, nothing further happened.
The year 1902 was one in which the centenary of Abel's birth was celebrated. King Oscar II become interested in a prize in Abel's honour. In close association with the Science Society of Christiania, today the Norwegian Academy of Science and Letters, the mathematicians Carl Størmer and Ludvig Sylow drew up statutes and rules for this prize. However, the dissolution of the union between Sweden and Norway in 1905 put an end to any further plans. Fridtjof Nansen, the polar explorer, regretted that even with contributions from mathematics circles abroad, it was financially impossible for Norway to establish an Abel fund on its own. In a letter in 1906 to the mathematician Elling Holst he added: "The Abel Prize promised by blessed King Oscar went to heaven with the Union."
With the bicentenary of Abel's birth approaching, Arild Stubhaug, who had written a major new biography of Abel, made another attempt to set up an Abel Prize. At a meeting in August 2000 between Stubhaug and the CEO of Telenor, Tormod Hermansen, events from a century earlier were discussed and the plans for a major international Abel Prize dusted off. Hermansen briefed the Ministry of Education, Research and Church Affairs about the idea, and Stubhaug brought the matter before the Department of Mathematics at the University of Oslo. After an invitation from Arne Bang Huseby, the academic head of department, and Yngvar Reichelt, the administrative head of department, Hermansen, along with his secretary, Kjell Stahl, attended a meeting at the Department of Mathematics in March 2001.
Here a working group was appointed, the Working Group for the Abel Prize, consisting of professors Jens Erik Fenstad, Arnfinn Laudal and Ragni Piene, administrative head of department Yngvar Reichelt, lecturer Nils Voje Johansen and the author Arild Stubhaug. From then on all parties involved worked intensely on the matter. Members of the Storting and key players in academic, business and cultural circles were briefed on the plans for an Abel Prize, and feedback was entirely positive. Declarations of support also came from major international mathematics organisations. On 23 May the Working Group for the Abel Prize sent the prime minister its proposal to establish an Abel Prize. In a speech on the campus of the University of Oslo in August 2001, the Norwegian Prime Minister announced that the Government would establish an Abel Fund. He emphasised the broad political consensus regarding the proposal and hoped that an annual Abel Prize would strengthen and inspire teaching as well as scientific efforts. The incoming Bondevik II government upheld the proposal. The Storting (Parliament) agreed with the government's proposal and the award was established in 2002. The first Abel Prize laureate was Jean-Pierre Serre in 2003.
8.2. Michel Talagrand awarded the 2024 Abel Prize.
The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2024 to Michel Talagrand of the French National Centre for Scientific Research (CNRS), Paris, France:-
The modern world is a constant flow of random events, and understanding that randomness has impacts on everything from business logistics to condensed-matter physics. Much of Talagrand's work involves understanding and utilising the "Gaussian distribution", often better known as the "normal distribution" or - thanks to its shape - the "bell curve". Our whole life is guided by the Gaussian distribution: the weight of babies at birth, the test results students get at school and the ages athletes retire at are all seemingly random events that neatly follow the Gaussian distribution.
Three specific areas
The Abel Prize is given for three specific areas of Talagrand's work:
Suprema of stochastic processes - A stochastic process produces a sequence of random values, and the "supremum" is the largest value to be expected from a collection of those values. If the height of waves crashing on a beach is a stochastic process, it is useful to know what the largest wave to hit the beach next year is likely to be.
Concentration of measures - Counterintuitively, when a process depends on a range of different sources of randomness, instead of getting more complicated, it is possible for the different random factors to compensate for each other and produce more predictable results. Talagrand has given sharp quantitative estimates for this.
Spin glass - Leaving abstract probability theory behind, a "spin glass" is a special form of matter that atoms can arrange themselves in, much to the initial surprise of physicists. Talagrand used his knowledge of statistics and probability to prove limits on how spin glass matter can behave, and thereby completed the proof of Giorgio Parisi's Nobel Prize winning work (2021).
"Talagrand is an exceptional mathematician, and a formidable problem solver. He has made profound contributions to our understanding of random, and in particular, Gaussian, processes. His work has reshaped several areas of probability theory. Furthermore, his proof of the celebrated Parisi formula for free energy of spin glasses is an amazing accomplishment," says Professor Helge Holden, chair of the Abel Prize Committee.
"Become rich with my prizes"
Michel Talagrand was born in 1952 in France, and he obtained his PhD in mathematics in 1977 from the University of Paris VI. He spent some years at Ohio State University in the US. He is married and has two sons. He is a member of the French Academy of Sciences. He has received numerous awards, and on his website he invites the mathematical community to solve puzzles under the heading "Become rich with my prizes".
Transforming results
"Talagrand is an outstanding and highly productive mathematician whose work has transformed probability theory, functional analysis and statistics. He has had an enormous impact on mathematics and its applications," says Lise Øvreas, president of the Norwegian Academy of Science and Letters.
8.3. Citation for Michel Talagrand.
The development of probability theory was originally motivated by problems that arose in the context of gambling or assessing risks. It has now become apparent that a thorough understanding of random phenomena is essential in today's world. For example, random algorithms underpin our weather forecast and large language models. In our quest for miniaturisation, we must consider effects like the random nature of impurities in crystals, thermal fluctuations in electric circuits, and decoherence of quantum computers. Talagrand has tackled many fundamental questions arising at the core of our mathematical description of such phenomena.
One of the threads running through Talagrand's work is to understand geometric properties of a high-dimensional phenomenon and to crystallise this into sharp estimates with broad scopes of applicability. This led him to obtain many influential inequalities. For instance, Talagrand derived powerful quantitative results to prove the sharp threshold phenomena that often appear in the study of phase transitions in statistical mechanics. He also obtained a useful inequality bounding the quadratic transportation cost distance between a probability measure and a Gaussian distribution by their relative entropy.
Much of Talagrand's work concerns the geometry of stochastic processes. A classical problem going back to Kolmogorov - arising for instance when one wants to analyse regularity properties of stochastic processes - is to estimate the supremum of a large collection of correlated random variables. Building on the works of Fernique and Dudley, Talagrand developed his theory of generic chaining, which provides sharp upper and lower bounds on the expectation of suprema of Gaussian processes. This illuminated the mysterious connection between the distance function (on the underlying index set) determined by the covariance of the process and the expectation of its supremum.
A key result in probability theory is the law of large numbers asserting that the normalised sum of independent random variables converges towards its mean. This normalised sum is therefore concentrated, using the terminology coined in the early work of Milman, or self-averaging, using physics terminology. It was gradually realised that concentration is ubiquitous, since many random variables defined as functions of a large number of independent random variables appeared to be close to their mean with high probability. In an amazing tour de force, Talagrand provided quantitative versions of this phenomenon that hold in great generality, including the case of discrete random variables. This result applies to functions of independent variables that are Lipschitz with respect to the Euclidean metric and convex, yielding one of several celebrated "Talagrand inequalities." It laid the groundwork for a non-asymptotic theory of independence applicable to high-dimensional statistical problems.
Since the works of Edwards and Anderson, physicists have been fascinated by the complex behaviour exhibited by disordered systems, which describe phenomena like magnetisation in the presence of impurities, and more recently also the energy landscapes arising in machine learning. In 1980, Parisi (Nobel Prize in Physics, 2021) proposed an expression for the free energy of one of the simplest models of this type, namely the Sherrington-Kirkpatrick model. Guerra showed rigorously that this formula is an upper bound for the free energy. In a groundbreaking article, Talagrand proved the complementary lower bound, hence completing the proof of the Parisi formula. This provided the foundation for the development of a mathematical theory of spin glasses and its applications in statistical learning.
Talagrand also obtained a rich variety of important results in measure theory and functional analysis. To cite only the most recent one, he answered a longstanding question by von Neumann and Maharam in the negative by showing that there exist submeasures which are exhaustive, but are not absolutely continuous with respect to any finitely additive measure. This fact implies the existence of radically new Boolean algebras.
Talagrand is an exceptionally prolific mathematician whose work has transformed probability theory, functional analysis, and statistics. His research is characterised by a desire to understand interesting problems at their most fundamental level, building new mathematical theories along the way. He disseminated many of his insights in the form of very influential research monographs. Combining technical virtuosity with deep analytical and geometric insights to construct new powerful tools and answer longstanding hard questions, Michel Talagrand has had and continues to have an enormous impact on mathematics and its applications.
8.4. Michel Talagrand: A brief biography.
The Abel Prize Laureate of 2024, Michel Talagrand, has stated that he always worked on the problems he enjoyed the most, following his own preference. Given this attitude, where hard work and pleasure seem to merge, it is hardly surprising that Talagrand is also a marathon runner and has travelled to more than a hundred countries with his family. The Abel Prize 2024 is a confirmation of the fact that his joyous efforts have made a lasting mark on the field of mathematics.
Michel Talagrand was born on 15 February 1952 in France. He grew up in Lyon together with a younger sister, a father who was a professor of mathematics and a mother who was a teaching French.
At age five he lost an eye due to a genetic illness. Ten years later his other eye was at risk, and he missed school for six months. Because of his fear of going blind, he studied hard during this period, and thus discovered his talent for mathematics and physics. He later studied mathematics at the local University of Lyon.
In 1974 he was offered a research position at the National Centre of Scientific Research (CNRS) in Paris, and completed his PhD in 1977. His affiliation lasted until his retirement in 2017. He was a member of the Functional Analysis Team of the Institute for Mathematical Sciences, and, from 1985 onward, research director at CNRS. Early in his career he worked with and was influenced by Gustave Choquet, Gilles Pisier and Vitali Milman.
He is married to Wansoo Rhee, a now retired professor of management science at Ohio State University, whom he met on his first ever trip to the USA. They have two sons.
Talagrand's mathematical style is atypical. He does not mind studying small problems as stepping stones to further significant discoveries. He has himself written of his method that: "it helps to be humble and to start by understanding fully the simple situations. When working on a conjecture I also found it helpful to alternatively try to prove it and try to disprove it. The progress comes by jumps, much like matching two pieces of a puzzle. This is nearly instantaneous. Now you see it, and the moment before you did not. After such progress, you may have a much clearer vision of the problem."
Besides a rich bibliography, Talagrand also invested in the exposition of his results and achievements. His books on The Generic Chaining and Spin Glasses are authoritative references in these fields. The introduction volume to Quantum Field Theory represents another aspect of his interests and contributions which will be relevant to numerous researchers. Talagrand's impressive achievements, illustrated by breakthrough solutions to fundamental conjectures, and invention of new, basic and deep inequalities, have been foundational and extremely influential, with a wide and deep impact.
Talagrand was elected as fellow of the French Scientific Academy in 2004 and is Chevalier de la Légion d'Honneur since 2011. He has received several awards including the Loève prize (1995), the Fermat Prize (1997) and the Shaw Prize (2019).
After receiving the Shaw prize money, he invited the mathematical community to win rewards by solving puzzles published on his web site under the heading "Become rich with my prizes". His playful approach to both life and science is also clear to be seen in the first statement on his web page: "Mathematics gives you wings" - linking to the painting "Allegory of Divine Wisdom" (1680s) by Luca Giordano. Talagrand's mathematical wisdom has certainly taken him far.
8.5. Talagrand and his mathematics, by Arne B Sletsjøe.
The Abel Committee says in the citation: "The development of probability theory was originally motivated by problems that arose in the context of gambling or assessing risk. It has now become apparent that a thorough understanding of random phenomena is essential in today's world. For example, random algorithms underpin our weather forecast and large language models. In our quest for miniaturisation, we must consider effects like the random nature of impurities in crystals, thermal fluctuations in electric circuits, and decoherence of quantum computers. Talagrand has tackled many fundamental questions arising at the core of our mathematical description of such phenomena."
In 2007, S R Srinivasa Varadhan was awarded the Abel Prize, also for his contributions to probability theory. The connection between the two laureates can be illustrated by the law of large numbers. The law of large numbers was first proved by the Swiss mathematician Jacob
Bernoulli in his treatise Ars Conjectandi, published in 1713, 8 years after his death, studies an event that occurs with a certain probability, but the probability is unfortunately unknown to him. His aim is therefore to estimate the probability as the fraction of the number of times the event occurs by the number of times the experiment is repeated.
Bernoulli's task is to estimate the proportion of white balls in an urn that contains an unknown number of white and black balls. His strategy is to draw a sequence of balls from the urn, putting the ball back after each draw, and estimate the unknown proportion of white balls in the urn by the proportion of the balls drawn that are white. Bernouilli shows, by choosing large enough, that he can obtain any desired accuracy and reliability for the estimate. This is precisely the weak version of the law of large numbers.
The law tells us that the probability of the difference between the mean and the expectation being less than some chosen value, is as close to 1 as we would like, provided we repeat the experiment sufficiently many times. If we have found twice as many white as black balls after a large number of trials, we have increasing evidence for the same proportion inside the urn. Among the important contributions by Talagrand we find a variety of results gathered under the umbrella "Talagrand's inequalities". The deviation from the expected value in the law of large numbers is an archetype of an inequality in this context; give an upper bound for the probability of a given deviation as a function of the probability of the event and the number of repetitions of the event.
Former Abel Prize laureate Varadhan studied the tail of the probability distribution, i.e. the occurrence of events outside of the range of the inequality, popularly stated as "the unexpected is also expected". Varadhan's approach can be illustrated by one of the headaches of the insurance company; how can we be prepared for the unexpected, like a 100-year flood or an earthquake in a geologically stable area? Talagrand's approach is to give a range where the actual probability model is likely to be valid, e.g. how precise is the weather forecast or to what extent can we know that the AI robot is not hallucinating?
Transportation costs between measures
Another important contribution mentioned by the Abel Committee is "a useful inequality bounding the quadratic transportation cost distance between a probability measure and a Gaussian distribution by their relative entropy." To a non-expert this might seem more like a collection of strange word, rather than a reasonable sentence.
The content of that phrase can be illustrated by the following example: The portfolio of the NOK 17-trillion Norwegian Government Pension Fund Global is spread over a large number of investments. Every day the analysts trade shares and bonds in a large scale, trying to optimise the return of the fund. Every transaction has an individual cost, and an important challenge for the analysts is to decide how to "restructure" the portfolio to the lowest possible total cost. If we say that the total amount of money in the fund is 1, we can consider the portfolio as a probability distribution over the set of banks, funds, companies and other investment objects. The profile of the portfolio two consecutive days describes two different probability measures on the same set, and the strategy for how to move money between the investment objects has a price, given by the cost function. Thus, each moving strategy has an individual cost.
We can "apply" Talagrand's inequality for the bounding of transportation cost to this illustrating example. The result would then say that the optimal solution to minimising the transportation cost for the rearrangement of the portfolio is essentially bounded by a numerical value for the dependence of the two portfolio distributions. This numerical value is what is called the relative entropy. It measures essentially the difference between two profiles of the portfolio. If the profiles of the portfolio are the same, then there are no transportation costs between them. If the variation is significant, the transportation cost will increase. In both cases, the transportation costs are essentially controlled by the relative entropy of the two profiles, as pointed out by Talagrand.
Bounds of the free energy for spin glasses
Another quote from the citation, referring to the Parisi formula for the Sherrington-Kirkpatrick model for the free energy of spin glass: "... this formula is an upper bound for the free energy. In a groundbreaking article, Talagrand proved the complementary lower bound, hence completing the proof of the Parisi formula."
Spin glasses are alloys formed by noble metals in which a small amount of iron is dissolved. The iron molecules are too distant to really affect each other, and it is only when influenced by an external magnetic field they close the ranks and becomes a nice ferromagnet. Spin glasses differ from their ferromagnetic relatives by the fact that when the external field is removed, the magnetisation of the spin glasses will decrease rapidly. The phenomenon is described by considerations around the free energy of the system. The Parisi formula for the Sherrington-Kirkpatrick model refers to a long-standing conjecture about the bounds of the free energy.
Mathematically we can consider the spin of each iron molecule as a random variable. The macroscopic behaviour of the spin glass is therefore related to the asymptotic values of a large number of weakly correlated random variables. This indicates the link to the interests of this year's Abel Laureate. Talagrand's proof of the Parisi formula is a manifestation of how mathematical theory can contribute to increased knowledge in subjects outside mathematics.
8.6. Stochastic processes, by Arne B Sletsjøe.
"Much of Talagrand's work concerns the geometry of stochastic processes." (quote from the citation of The Abel Committee) If you toss a coin once it can either show head or tail. For computational reasons we rename head as 1 and tail as 0. The two outcomes have equal probability, i.e. one half each. The expected value is the sum of products of outcome times probability. For the tossing of a coin the expected value is , even though this value is never achieved.
If we instead use 10 coins, or toss a coin 10 times, we can compute an outcome by counting the number of heads and divide by 10, the number of tosses. The expected value is still 1 2 , but now this value is achievable if the experiment results in 5 heads and 5 tails. Out of the 1024 possible outcomes of the 10 tosses, 252 or approximately 25% will contain 5 heads and 5 tails. If we expand the acceptable outcome range to include also 4 or 6 heads, the success rate jumps up to approximately 66%. The mean value of heads for 10 coins is 5, so 4 or 6 can be thought of as 20% off the mean. For 20 coins a deviation less than 20% off the mean correspond to 8, 9, 10, 11 or 12 heads out of 20. A computation shows that in this case these number of heads takes up around 75% of all possible outcomes. If we increase the number of coins even more, this percentage will also increase and approach 1, as we increase the number of tosses.
We can generalise this example by replacing the tossing of a coin by a stochastic variable. A stochastic or random variable is a variable whose values randomly change according to some probability distribution law. The set of values the stochastic variable can assume is called the sample space. The stochastic variable which models tossing of coins has a sample space of two elements; {Head, Tail}, with equal probability. Notice also that the outcome of one tossing is independent of the outcome of all the others.
In a more general setting the sample space is likely to be much more complicated than the two outcomes of a coin tossing. Throwing a dice will give a sample space of 6 outcomes, while the price of a share on the stock exchange can vary over a rather large range. But unlike the coin or the dice, the price of the share measured day by day is not an independent variable. The price the next day will not differ very much from the day before. The stochastic variables are correlated.
Talagrand has been interested in this problem, and provided important results for the bound of a large collection of correlated random variables.
8.7. Concentration of measure, by Arne B Sletsjøe.
A disk of radius 1 (unit disk) can be described as the set of points in the plane such that . The area of the unit disk is very well known to be . Inside the unit disk we place a concentric disk of radius for some arbitrary small positive number . The area of this smaller disk is and the area of the annulus is . As a fraction of the total area the inner disk counts for . If we do the same construction for a solid ball, given by , the fraction of the inner ball of radius versus the unit ball is . For for a 4-ball of radius R in and volume , the fraction is . The corresponding fraction for a -ball, given as the zero set of the equation in the Euclidian space is . The consequence is that for a high-dimensional sphere, where we let grow towards , almost all of its volume will be concentrated in a thin annulus.
In a similar way one can show that for high-dimensional spheres almost all of its surface will be concentrated in a small belt around equator.
An other strange phenomenon in high-dimensional geometry concerns the volume of a -sphere of radius 1. The volume is proportional to , which grows without any limit when increases.
In the citation the Abel committee says: "One of the threads running through Talagrand's work is to understand geometric properties of a high-dimensional phenomenon and to crystallise this into sharp estimates with broad scopes of applicability." The example above concerning high-dimensional spheres goes into the core of this quote.
We can give a more general description of the "concentration of measure phenomenon": Suppose we have given a large number of "nice" random variables, and consider their sum. If the random variables are sufficiently independent, the sum will sharply concentrate in an interval which is much narrower than one should expect by the first glance.
8.8. A Glimpse of the Laureate's Work, by Matt Parker.
Michel Talagrand is an expert at understanding and taming complicated random processes. Randomness can arise in a wide range of ways, and Talagrand has explored many different types. One of the most common, and arguably most important, types of randomness arises from "Gaussian processes". The Gaussian distribution has been a constant feature of Talagrand's career so it's worth considering it as a tangible example when exploring his work.
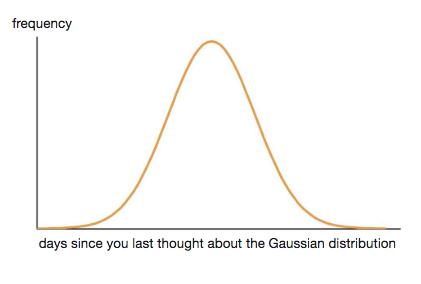
A Gaussian distribution (sometimes called the "normal distribution" or "bell curve") occurs with surprising frequency in the world around us. The mass of babies at birth, the test results students get at school and the ages athletes retire at are all seemingly random things which neatly follow the Gaussian distribution. These are characterised by having an average in the middle which most values are close to, and then decreasing numbers of cases as values move further above and below the average.
When observing a random process there are some things which it could be nice to know. For example, if you take the average of the values being produced, how close is that likely to be to the true average value of the underlying Gaussian process? How big or small are the possible values in the future likely to be?
Talagrand produced rigorous and tight thresholds with specific uncertainties so when these kind of random, stochastic processes are observed we know exactly how confident we can reasonably be about what the process will do going forward.
Viewing Talagrand's work through the example of a single Gaussian distribution is an extreme oversimplification of how general and wide ranging his results were. More complicated situations involve several different random variables, with different distributions that combine in complicated ways. Instead of being a simple distribution, if each random variable is considered to be an independent axis, the total probability space which results is a multi-dimensional object, beyond direct human comprehension.
Talagrand was able to probe and understand these higher dimensional spaces. Asking probabilities questions about these spaces is akin to trying to find their higher dimensional volumes, and area of mathematics called "measure theory". In simple 2D space, we can understand area as the sum of the areas if we split a distribution up into tiny squares and then count all of them. In higher dimensions, it is not that simple to work out the measure of a set of points. The Banach-Tarski paradox is a famous result that if you are not careful: a ball can be split into pieces which actually total twice its original volume.
The challenge becomes finding spaces which are well behaved enough to have a meaningful measure, and then set bounds on what that measure can be. Talagrand was able to do this with spaces beyond what human intuition is capable of dealing with. These higher dimension shapes can behave in very surprising ways.
Talagrand's work converting these objects into probability insights often involve knowing where the hyper-volume was likely to be concentrated around. Which for something like a ball, it would seem obvious: a ball is defined as all the points within the radius distance of a central point. But that can be deceiving.
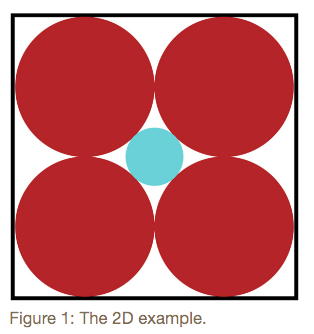
Imaging a 2D ball, a circular disk, trapped between four unit disks, surrounded by a box (see Figure 1). The biggest radius that central circle can possibly have is 0.41421, which is much smaller than the unit circles around it.
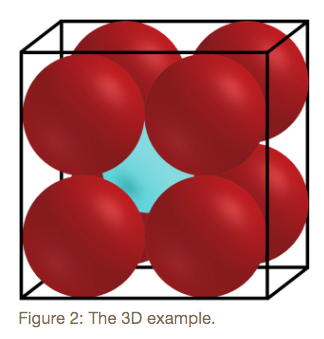
In 3D we can pack a box with eight unit spheres (see Figure 2) and the smallest sphere which can sit in the very middle would have a radius of 0.73205. Which is slightly bigger than the 2D case. But our human intuition is that while there may be a bit more wriggle room with the extra dimensions, ultimately the central sphere will remain bounded.
This is absolutely not the case. In 4D the sixteen unit spheres in a box allow enough space for a central sphere the same size as them: with a radius of 1. By 10D that central sphere is so big it reaches outside the box and by 26D it is twice as wide as the box.
The 'shape' and distribution of content within a higher dimension sphere does not match what we expect. In one (technically incorrect but still slightly illuminating) sense, spheres are more spiky than we think, with thin extremities which can reach through and pack around other objects. In another less incorrect sense: spheres in this high dimensions becomes all outer shell and very little internal, central volume.
Talagrand worked with shapes such as these, finding new and novel ways to put limits on where the bulk of a probability distribution could be.
The ubiquity of Gaussian processes means there are many possible applications of Talagrand's work. One specific one is the condensed matter physics problem of a "spin glass". This is an arrangement of matter which is not a 'glass' like in a window, but rather a random structure of magnetic moments.
Spin glasses sit between the highly organised magnetic properties of ferromagnet materials and the random arrangement of paramagnetic materials. If a ferromagnetic substance is heated and an external magnetic field used to align all the internal magnetic moment, this neat alignment will persist even after the substance is cooled. A paramagnetic substance will exponentially lose its internal magnetic field once the external field is removed. A spin glass however, will also lose its own magnetic arrangement but at a rate and in a way which currently defies our understanding.
The internal magnetic structures within a spin glass are arranged randomly, but with some order which causes their complex behaviours.
Physicists developed theories and limits on how this randomness would behave. Talagrand was able to come in and, despite ignoring the physics, use mathematics to provide a solid proof that the limits were indeed correct.
Michel Talagrand's work in probability theory and related areas has produced several key insights and proofs using novel techniques. These would be beautiful in their own mathematical right, but the direct application to physical systems makes these results extra meaningful.
8.9. Talagrand's reaction to being awarded the Abel Prize.
I think everybody would agree that the Abel prize is really considered like the equivalent of the Nobel prize in mathematics. So it's something for me totally unexpected, I never, ever dreamed I would receive this prize. And actually, it's not such an easy thing to do, because there is this list of people who already received it. And on that list, there are true giants of mathematics. And it's not such a comfortable feeling to sit with them, let me tell you, because it's clear that their achievements are on an entirely other scale than mine.
The Abel Prize was awarded for the first time in 2003 but it was first suggested over 100 years earlier. Sophus Lie, when he saw that Nobel's plans for annual prizes did not include one for mathematics, proposed the setting up of an Abel Prize which would be awarded every five years for outstanding work in pure mathematics. Lie's effort was, by all accounts, inspired by the ongoing collection for the Nansen Fund and he contacted mathematicians world-wide and gathered wide support. However he had not set up any machinery to carry the idea forward and when he died soon after this, in 1899, nothing further happened.
The year 1902 was one in which the centenary of Abel's birth was celebrated. King Oscar II become interested in a prize in Abel's honour. In close association with the Science Society of Christiania, today the Norwegian Academy of Science and Letters, the mathematicians Carl Størmer and Ludvig Sylow drew up statutes and rules for this prize. However, the dissolution of the union between Sweden and Norway in 1905 put an end to any further plans. Fridtjof Nansen, the polar explorer, regretted that even with contributions from mathematics circles abroad, it was financially impossible for Norway to establish an Abel fund on its own. In a letter in 1906 to the mathematician Elling Holst he added: "The Abel Prize promised by blessed King Oscar went to heaven with the Union."
With the bicentenary of Abel's birth approaching, Arild Stubhaug, who had written a major new biography of Abel, made another attempt to set up an Abel Prize. At a meeting in August 2000 between Stubhaug and the CEO of Telenor, Tormod Hermansen, events from a century earlier were discussed and the plans for a major international Abel Prize dusted off. Hermansen briefed the Ministry of Education, Research and Church Affairs about the idea, and Stubhaug brought the matter before the Department of Mathematics at the University of Oslo. After an invitation from Arne Bang Huseby, the academic head of department, and Yngvar Reichelt, the administrative head of department, Hermansen, along with his secretary, Kjell Stahl, attended a meeting at the Department of Mathematics in March 2001.
Here a working group was appointed, the Working Group for the Abel Prize, consisting of professors Jens Erik Fenstad, Arnfinn Laudal and Ragni Piene, administrative head of department Yngvar Reichelt, lecturer Nils Voje Johansen and the author Arild Stubhaug. From then on all parties involved worked intensely on the matter. Members of the Storting and key players in academic, business and cultural circles were briefed on the plans for an Abel Prize, and feedback was entirely positive. Declarations of support also came from major international mathematics organisations. On 23 May the Working Group for the Abel Prize sent the prime minister its proposal to establish an Abel Prize. In a speech on the campus of the University of Oslo in August 2001, the Norwegian Prime Minister announced that the Government would establish an Abel Fund. He emphasised the broad political consensus regarding the proposal and hoped that an annual Abel Prize would strengthen and inspire teaching as well as scientific efforts. The incoming Bondevik II government upheld the proposal. The Storting (Parliament) agreed with the government's proposal and the award was established in 2002. The first Abel Prize laureate was Jean-Pierre Serre in 2003.
8.2. Michel Talagrand awarded the 2024 Abel Prize.
The Norwegian Academy of Science and Letters has decided to award the Abel Prize for 2024 to Michel Talagrand of the French National Centre for Scientific Research (CNRS), Paris, France:-
... for his groundbreaking contributions to probability theory and functional analysis, with outstanding applications in mathematical physics and statistics.Michel Talagrand receives the prize for his work in probability theory and stochastic processes. From the outset, the development of probability theory was motivated by problems that arose in the context of gambling or assessing risks. The common theme in Michel Talagrand's groundbreaking discoveries is working with and understanding the random processes we see all around us. It has now become apparent that a thorough understanding of random phenomena is essential in today's world. For example, random algorithms underpin our weather forecasting and large language models.
The modern world is a constant flow of random events, and understanding that randomness has impacts on everything from business logistics to condensed-matter physics. Much of Talagrand's work involves understanding and utilising the "Gaussian distribution", often better known as the "normal distribution" or - thanks to its shape - the "bell curve". Our whole life is guided by the Gaussian distribution: the weight of babies at birth, the test results students get at school and the ages athletes retire at are all seemingly random events that neatly follow the Gaussian distribution.
Three specific areas
The Abel Prize is given for three specific areas of Talagrand's work:
Suprema of stochastic processes - A stochastic process produces a sequence of random values, and the "supremum" is the largest value to be expected from a collection of those values. If the height of waves crashing on a beach is a stochastic process, it is useful to know what the largest wave to hit the beach next year is likely to be.
Concentration of measures - Counterintuitively, when a process depends on a range of different sources of randomness, instead of getting more complicated, it is possible for the different random factors to compensate for each other and produce more predictable results. Talagrand has given sharp quantitative estimates for this.
Spin glass - Leaving abstract probability theory behind, a "spin glass" is a special form of matter that atoms can arrange themselves in, much to the initial surprise of physicists. Talagrand used his knowledge of statistics and probability to prove limits on how spin glass matter can behave, and thereby completed the proof of Giorgio Parisi's Nobel Prize winning work (2021).
"Talagrand is an exceptional mathematician, and a formidable problem solver. He has made profound contributions to our understanding of random, and in particular, Gaussian, processes. His work has reshaped several areas of probability theory. Furthermore, his proof of the celebrated Parisi formula for free energy of spin glasses is an amazing accomplishment," says Professor Helge Holden, chair of the Abel Prize Committee.
"Become rich with my prizes"
Michel Talagrand was born in 1952 in France, and he obtained his PhD in mathematics in 1977 from the University of Paris VI. He spent some years at Ohio State University in the US. He is married and has two sons. He is a member of the French Academy of Sciences. He has received numerous awards, and on his website he invites the mathematical community to solve puzzles under the heading "Become rich with my prizes".
Transforming results
"Talagrand is an outstanding and highly productive mathematician whose work has transformed probability theory, functional analysis and statistics. He has had an enormous impact on mathematics and its applications," says Lise Øvreas, president of the Norwegian Academy of Science and Letters.
8.3. Citation for Michel Talagrand.
The development of probability theory was originally motivated by problems that arose in the context of gambling or assessing risks. It has now become apparent that a thorough understanding of random phenomena is essential in today's world. For example, random algorithms underpin our weather forecast and large language models. In our quest for miniaturisation, we must consider effects like the random nature of impurities in crystals, thermal fluctuations in electric circuits, and decoherence of quantum computers. Talagrand has tackled many fundamental questions arising at the core of our mathematical description of such phenomena.
One of the threads running through Talagrand's work is to understand geometric properties of a high-dimensional phenomenon and to crystallise this into sharp estimates with broad scopes of applicability. This led him to obtain many influential inequalities. For instance, Talagrand derived powerful quantitative results to prove the sharp threshold phenomena that often appear in the study of phase transitions in statistical mechanics. He also obtained a useful inequality bounding the quadratic transportation cost distance between a probability measure and a Gaussian distribution by their relative entropy.
Much of Talagrand's work concerns the geometry of stochastic processes. A classical problem going back to Kolmogorov - arising for instance when one wants to analyse regularity properties of stochastic processes - is to estimate the supremum of a large collection of correlated random variables. Building on the works of Fernique and Dudley, Talagrand developed his theory of generic chaining, which provides sharp upper and lower bounds on the expectation of suprema of Gaussian processes. This illuminated the mysterious connection between the distance function (on the underlying index set) determined by the covariance of the process and the expectation of its supremum.
A key result in probability theory is the law of large numbers asserting that the normalised sum of independent random variables converges towards its mean. This normalised sum is therefore concentrated, using the terminology coined in the early work of Milman, or self-averaging, using physics terminology. It was gradually realised that concentration is ubiquitous, since many random variables defined as functions of a large number of independent random variables appeared to be close to their mean with high probability. In an amazing tour de force, Talagrand provided quantitative versions of this phenomenon that hold in great generality, including the case of discrete random variables. This result applies to functions of independent variables that are Lipschitz with respect to the Euclidean metric and convex, yielding one of several celebrated "Talagrand inequalities." It laid the groundwork for a non-asymptotic theory of independence applicable to high-dimensional statistical problems.
Since the works of Edwards and Anderson, physicists have been fascinated by the complex behaviour exhibited by disordered systems, which describe phenomena like magnetisation in the presence of impurities, and more recently also the energy landscapes arising in machine learning. In 1980, Parisi (Nobel Prize in Physics, 2021) proposed an expression for the free energy of one of the simplest models of this type, namely the Sherrington-Kirkpatrick model. Guerra showed rigorously that this formula is an upper bound for the free energy. In a groundbreaking article, Talagrand proved the complementary lower bound, hence completing the proof of the Parisi formula. This provided the foundation for the development of a mathematical theory of spin glasses and its applications in statistical learning.
Talagrand also obtained a rich variety of important results in measure theory and functional analysis. To cite only the most recent one, he answered a longstanding question by von Neumann and Maharam in the negative by showing that there exist submeasures which are exhaustive, but are not absolutely continuous with respect to any finitely additive measure. This fact implies the existence of radically new Boolean algebras.
Talagrand is an exceptionally prolific mathematician whose work has transformed probability theory, functional analysis, and statistics. His research is characterised by a desire to understand interesting problems at their most fundamental level, building new mathematical theories along the way. He disseminated many of his insights in the form of very influential research monographs. Combining technical virtuosity with deep analytical and geometric insights to construct new powerful tools and answer longstanding hard questions, Michel Talagrand has had and continues to have an enormous impact on mathematics and its applications.
8.4. Michel Talagrand: A brief biography.
The Abel Prize Laureate of 2024, Michel Talagrand, has stated that he always worked on the problems he enjoyed the most, following his own preference. Given this attitude, where hard work and pleasure seem to merge, it is hardly surprising that Talagrand is also a marathon runner and has travelled to more than a hundred countries with his family. The Abel Prize 2024 is a confirmation of the fact that his joyous efforts have made a lasting mark on the field of mathematics.
Michel Talagrand was born on 15 February 1952 in France. He grew up in Lyon together with a younger sister, a father who was a professor of mathematics and a mother who was a teaching French.
At age five he lost an eye due to a genetic illness. Ten years later his other eye was at risk, and he missed school for six months. Because of his fear of going blind, he studied hard during this period, and thus discovered his talent for mathematics and physics. He later studied mathematics at the local University of Lyon.
In 1974 he was offered a research position at the National Centre of Scientific Research (CNRS) in Paris, and completed his PhD in 1977. His affiliation lasted until his retirement in 2017. He was a member of the Functional Analysis Team of the Institute for Mathematical Sciences, and, from 1985 onward, research director at CNRS. Early in his career he worked with and was influenced by Gustave Choquet, Gilles Pisier and Vitali Milman.
He is married to Wansoo Rhee, a now retired professor of management science at Ohio State University, whom he met on his first ever trip to the USA. They have two sons.
Talagrand's mathematical style is atypical. He does not mind studying small problems as stepping stones to further significant discoveries. He has himself written of his method that: "it helps to be humble and to start by understanding fully the simple situations. When working on a conjecture I also found it helpful to alternatively try to prove it and try to disprove it. The progress comes by jumps, much like matching two pieces of a puzzle. This is nearly instantaneous. Now you see it, and the moment before you did not. After such progress, you may have a much clearer vision of the problem."
Besides a rich bibliography, Talagrand also invested in the exposition of his results and achievements. His books on The Generic Chaining and Spin Glasses are authoritative references in these fields. The introduction volume to Quantum Field Theory represents another aspect of his interests and contributions which will be relevant to numerous researchers. Talagrand's impressive achievements, illustrated by breakthrough solutions to fundamental conjectures, and invention of new, basic and deep inequalities, have been foundational and extremely influential, with a wide and deep impact.
Talagrand was elected as fellow of the French Scientific Academy in 2004 and is Chevalier de la Légion d'Honneur since 2011. He has received several awards including the Loève prize (1995), the Fermat Prize (1997) and the Shaw Prize (2019).
After receiving the Shaw prize money, he invited the mathematical community to win rewards by solving puzzles published on his web site under the heading "Become rich with my prizes". His playful approach to both life and science is also clear to be seen in the first statement on his web page: "Mathematics gives you wings" - linking to the painting "Allegory of Divine Wisdom" (1680s) by Luca Giordano. Talagrand's mathematical wisdom has certainly taken him far.
8.5. Talagrand and his mathematics, by Arne B Sletsjøe.
The Abel Committee says in the citation: "The development of probability theory was originally motivated by problems that arose in the context of gambling or assessing risk. It has now become apparent that a thorough understanding of random phenomena is essential in today's world. For example, random algorithms underpin our weather forecast and large language models. In our quest for miniaturisation, we must consider effects like the random nature of impurities in crystals, thermal fluctuations in electric circuits, and decoherence of quantum computers. Talagrand has tackled many fundamental questions arising at the core of our mathematical description of such phenomena."
In 2007, S R Srinivasa Varadhan was awarded the Abel Prize, also for his contributions to probability theory. The connection between the two laureates can be illustrated by the law of large numbers. The law of large numbers was first proved by the Swiss mathematician Jacob
Bernoulli in his treatise Ars Conjectandi, published in 1713, 8 years after his death, studies an event that occurs with a certain probability, but the probability is unfortunately unknown to him. His aim is therefore to estimate the probability as the fraction of the number of times the event occurs by the number of times the experiment is repeated.
Bernoulli's task is to estimate the proportion of white balls in an urn that contains an unknown number of white and black balls. His strategy is to draw a sequence of balls from the urn, putting the ball back after each draw, and estimate the unknown proportion of white balls in the urn by the proportion of the balls drawn that are white. Bernouilli shows, by choosing large enough, that he can obtain any desired accuracy and reliability for the estimate. This is precisely the weak version of the law of large numbers.
The law tells us that the probability of the difference between the mean and the expectation being less than some chosen value, is as close to 1 as we would like, provided we repeat the experiment sufficiently many times. If we have found twice as many white as black balls after a large number of trials, we have increasing evidence for the same proportion inside the urn. Among the important contributions by Talagrand we find a variety of results gathered under the umbrella "Talagrand's inequalities". The deviation from the expected value in the law of large numbers is an archetype of an inequality in this context; give an upper bound for the probability of a given deviation as a function of the probability of the event and the number of repetitions of the event.
Former Abel Prize laureate Varadhan studied the tail of the probability distribution, i.e. the occurrence of events outside of the range of the inequality, popularly stated as "the unexpected is also expected". Varadhan's approach can be illustrated by one of the headaches of the insurance company; how can we be prepared for the unexpected, like a 100-year flood or an earthquake in a geologically stable area? Talagrand's approach is to give a range where the actual probability model is likely to be valid, e.g. how precise is the weather forecast or to what extent can we know that the AI robot is not hallucinating?
Transportation costs between measures
Another important contribution mentioned by the Abel Committee is "a useful inequality bounding the quadratic transportation cost distance between a probability measure and a Gaussian distribution by their relative entropy." To a non-expert this might seem more like a collection of strange word, rather than a reasonable sentence.
The content of that phrase can be illustrated by the following example: The portfolio of the NOK 17-trillion Norwegian Government Pension Fund Global is spread over a large number of investments. Every day the analysts trade shares and bonds in a large scale, trying to optimise the return of the fund. Every transaction has an individual cost, and an important challenge for the analysts is to decide how to "restructure" the portfolio to the lowest possible total cost. If we say that the total amount of money in the fund is 1, we can consider the portfolio as a probability distribution over the set of banks, funds, companies and other investment objects. The profile of the portfolio two consecutive days describes two different probability measures on the same set, and the strategy for how to move money between the investment objects has a price, given by the cost function. Thus, each moving strategy has an individual cost.
We can "apply" Talagrand's inequality for the bounding of transportation cost to this illustrating example. The result would then say that the optimal solution to minimising the transportation cost for the rearrangement of the portfolio is essentially bounded by a numerical value for the dependence of the two portfolio distributions. This numerical value is what is called the relative entropy. It measures essentially the difference between two profiles of the portfolio. If the profiles of the portfolio are the same, then there are no transportation costs between them. If the variation is significant, the transportation cost will increase. In both cases, the transportation costs are essentially controlled by the relative entropy of the two profiles, as pointed out by Talagrand.
Bounds of the free energy for spin glasses
Another quote from the citation, referring to the Parisi formula for the Sherrington-Kirkpatrick model for the free energy of spin glass: "... this formula is an upper bound for the free energy. In a groundbreaking article, Talagrand proved the complementary lower bound, hence completing the proof of the Parisi formula."
Spin glasses are alloys formed by noble metals in which a small amount of iron is dissolved. The iron molecules are too distant to really affect each other, and it is only when influenced by an external magnetic field they close the ranks and becomes a nice ferromagnet. Spin glasses differ from their ferromagnetic relatives by the fact that when the external field is removed, the magnetisation of the spin glasses will decrease rapidly. The phenomenon is described by considerations around the free energy of the system. The Parisi formula for the Sherrington-Kirkpatrick model refers to a long-standing conjecture about the bounds of the free energy.
Mathematically we can consider the spin of each iron molecule as a random variable. The macroscopic behaviour of the spin glass is therefore related to the asymptotic values of a large number of weakly correlated random variables. This indicates the link to the interests of this year's Abel Laureate. Talagrand's proof of the Parisi formula is a manifestation of how mathematical theory can contribute to increased knowledge in subjects outside mathematics.
8.6. Stochastic processes, by Arne B Sletsjøe.
"Much of Talagrand's work concerns the geometry of stochastic processes." (quote from the citation of The Abel Committee) If you toss a coin once it can either show head or tail. For computational reasons we rename head as 1 and tail as 0. The two outcomes have equal probability, i.e. one half each. The expected value is the sum of products of outcome times probability. For the tossing of a coin the expected value is , even though this value is never achieved.
If we instead use 10 coins, or toss a coin 10 times, we can compute an outcome by counting the number of heads and divide by 10, the number of tosses. The expected value is still 1 2 , but now this value is achievable if the experiment results in 5 heads and 5 tails. Out of the 1024 possible outcomes of the 10 tosses, 252 or approximately 25% will contain 5 heads and 5 tails. If we expand the acceptable outcome range to include also 4 or 6 heads, the success rate jumps up to approximately 66%. The mean value of heads for 10 coins is 5, so 4 or 6 can be thought of as 20% off the mean. For 20 coins a deviation less than 20% off the mean correspond to 8, 9, 10, 11 or 12 heads out of 20. A computation shows that in this case these number of heads takes up around 75% of all possible outcomes. If we increase the number of coins even more, this percentage will also increase and approach 1, as we increase the number of tosses.
We can generalise this example by replacing the tossing of a coin by a stochastic variable. A stochastic or random variable is a variable whose values randomly change according to some probability distribution law. The set of values the stochastic variable can assume is called the sample space. The stochastic variable which models tossing of coins has a sample space of two elements; {Head, Tail}, with equal probability. Notice also that the outcome of one tossing is independent of the outcome of all the others.
In a more general setting the sample space is likely to be much more complicated than the two outcomes of a coin tossing. Throwing a dice will give a sample space of 6 outcomes, while the price of a share on the stock exchange can vary over a rather large range. But unlike the coin or the dice, the price of the share measured day by day is not an independent variable. The price the next day will not differ very much from the day before. The stochastic variables are correlated.
Talagrand has been interested in this problem, and provided important results for the bound of a large collection of correlated random variables.
8.7. Concentration of measure, by Arne B Sletsjøe.
A disk of radius 1 (unit disk) can be described as the set of points in the plane such that . The area of the unit disk is very well known to be . Inside the unit disk we place a concentric disk of radius for some arbitrary small positive number . The area of this smaller disk is a
In a similar way one can show that for high-dimensional spheres almost all of its surface will be concentrated in a small belt around equator.
An other strange phenomenon in high-dimensional geometry concerns the volume of a -sphere of radius 1. The volume is proportional to , which grows without any limit when increases.
In the citation the Abel committee says: "One of the threads running through Talagrand's work is to understand geometric properties of a high-dimensional phenomenon and to crystallise this into sharp estimates with broad scopes of applicability." The example above concerning high-dimensional spheres goes into the core of this quote.
We can give a more general description of the "concentration of measure phenomenon": Suppose we have given a large number of "nice" random variables, and consider their sum. If the random variables are sufficiently independent, the sum will sharply concentrate in an interval which is much narrower than one should expect by the first glance.
8.8. A Glimpse of the Laureate's Work, by Matt Parker.
Michel Talagrand is an expert at understanding and taming complicated random processes. Randomness can arise in a wide range of ways, and Talagrand has explored many different types. One of the most common, and arguably most important, types of randomness arises from "Gaussian processes". The Gaussian distribution has been a constant feature of Talagrand's career so it's worth considering it as a tangible example when exploring his work.

A Gaussian distribution (sometimes called the "normal distribution" or "bell curve") occurs with surprising frequency in the world around us. The mass of babies at birth, the test results students get at school and the ages athletes retire at are all seemingly random things which neatly follow the Gaussian distribution. These are characterised by having an average in the middle which most values are close to, and then decreasing numbers of cases as values move further above and below the average.
When observing a random process there are some things which it could be nice to know. For example, if you take the average of the values being produced, how close is that likely to be to the true average value of the underlying Gaussian process? How big or small are the possible values in the future likely to be?
Talagrand produced rigorous and tight thresholds with specific uncertainties so when these kind of random, stochastic processes are observed we know exactly how confident we can reasonably be about what the process will do going forward.
Viewing Talagrand's work through the example of a single Gaussian distribution is an extreme oversimplification of how general and wide ranging his results were. More complicated situations involve several different random variables, with different distributions that combine in complicated ways. Instead of being a simple distribution, if each random variable is considered to be an independent axis, the total probability space which results is a multi-dimensional object, beyond direct human comprehension.
Talagrand was able to probe and understand these higher dimensional spaces. Asking probabilities questions about these spaces is akin to trying to find their higher dimensional volumes, and area of mathematics called "measure theory". In simple 2D space, we can understand area as the sum of the areas if we split a distribution up into tiny squares and then count all of them. In higher dimensions, it is not that simple to work out the measure of a set of points. The Banach-Tarski paradox is a famous result that if you are not careful: a ball can be split into pieces which actually total twice its original volume.
The challenge becomes finding spaces which are well behaved enough to have a meaningful measure, and then set bounds on what that measure can be. Talagrand was able to do this with spaces beyond what human intuition is capable of dealing with. These higher dimension shapes can behave in very surprising ways.
Talagrand's work converting these objects into probability insights often involve knowing where the hyper-volume was likely to be concentrated around. Which for something like a ball, it would seem obvious: a ball is defined as all the points within the radius distance of a central point. But that can be deceiving.

Imaging a 2D ball, a circular disk, trapped between four unit disks, surrounded by a box (see Figure 1). The biggest radius that central circle can possibly have is 0.41421, which is much smaller than the unit circles around it.

In 3D we can pack a box with eight unit spheres (see Figure 2) and the smallest sphere which can sit in the very middle would have a radius of 0.73205. Which is slightly bigger than the 2D case. But our human intuition is that while there may be a bit more wriggle room with the extra dimensions, ultimately the central sphere will remain bounded.
This is absolutely not the case. In 4D the sixteen unit spheres in a box allow enough space for a central sphere the same size as them: with a radius of 1. By 10D that central sphere is so big it reaches outside the box and by 26D it is twice as wide as the box.
The 'shape' and distribution of content within a higher dimension sphere does not match what we expect. In one (technically incorrect but still slightly illuminating) sense, spheres are more spiky than we think, with thin extremities which can reach through and pack around other objects. In another less incorrect sense: spheres in this high dimensions becomes all outer shell and very little internal, central volume.
Talagrand worked with shapes such as these, finding new and novel ways to put limits on where the bulk of a probability distribution could be.
The ubiquity of Gaussian processes means there are many possible applications of Talagrand's work. One specific one is the condensed matter physics problem of a "spin glass". This is an arrangement of matter which is not a 'glass' like in a window, but rather a random structure of magnetic moments.
Spin glasses sit between the highly organised magnetic properties of ferromagnet materials and the random arrangement of paramagnetic materials. If a ferromagnetic substance is heated and an external magnetic field used to align all the internal magnetic moment, this neat alignment will persist even after the substance is cooled. A paramagnetic substance will exponentially lose its internal magnetic field once the external field is removed. A spin glass however, will also lose its own magnetic arrangement but at a rate and in a way which currently defies our understanding.
The internal magnetic structures within a spin glass are arranged randomly, but with some order which causes their complex behaviours.
Physicists developed theories and limits on how this randomness would behave. Talagrand was able to come in and, despite ignoring the physics, use mathematics to provide a solid proof that the limits were indeed correct.
Michel Talagrand's work in probability theory and related areas has produced several key insights and proofs using novel techniques. These would be beautiful in their own mathematical right, but the direct application to physical systems makes these results extra meaningful.
8.9. Talagrand's reaction to being awarded the Abel Prize.
I think everybody would agree that the Abel prize is really considered like the equivalent of the Nobel prize in mathematics. So it's something for me totally unexpected, I never, ever dreamed I would receive this prize. And actually, it's not such an easy thing to do, because there is this list of people who already received it. And on that list, there are true giants of mathematics. And it's not such a comfortable feeling to sit with them, let me tell you, because it's clear that their achievements are on an entirely other scale than mine.
Last Updated June 2025